【九-1】多元函数的基本概念--平面点集
内点;外点;边界点;连通集;等概念,考的不多
【九-2】n维空间
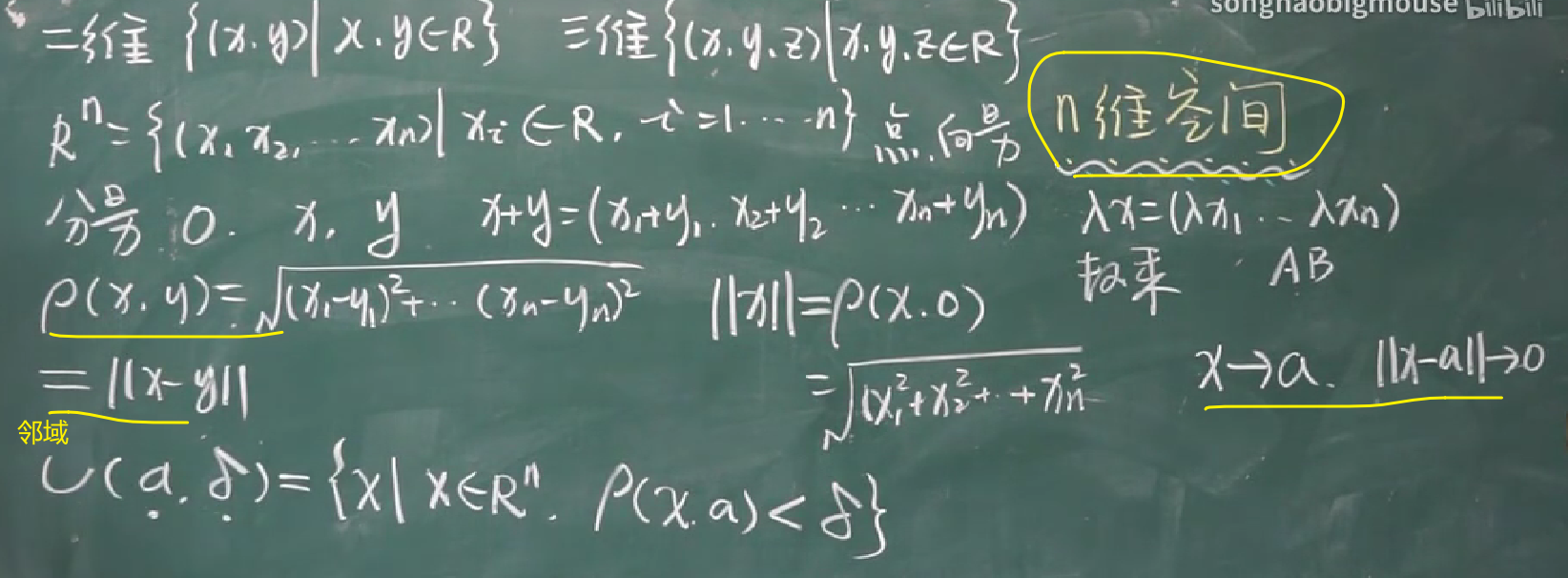
【九-3】多元函数的极限
类比一元函数的极限
【九-4】偏导数
定义;怎么求;几何意义;偏导数存在与连续的联系
【九-6】全微分
【九-7】多元复合函数求导(理论讲解)
【九-8】多元复合函数求导(例子讲解)
首先把函数的关系图画出来,然后写出求偏导的基本过程,慢慢求导即可
【九-9】隐函数求导(一个方程)

【九-10】隐函数求导(方程组)
用到行列式:出难题很难算;出简单吧又容易代入算出
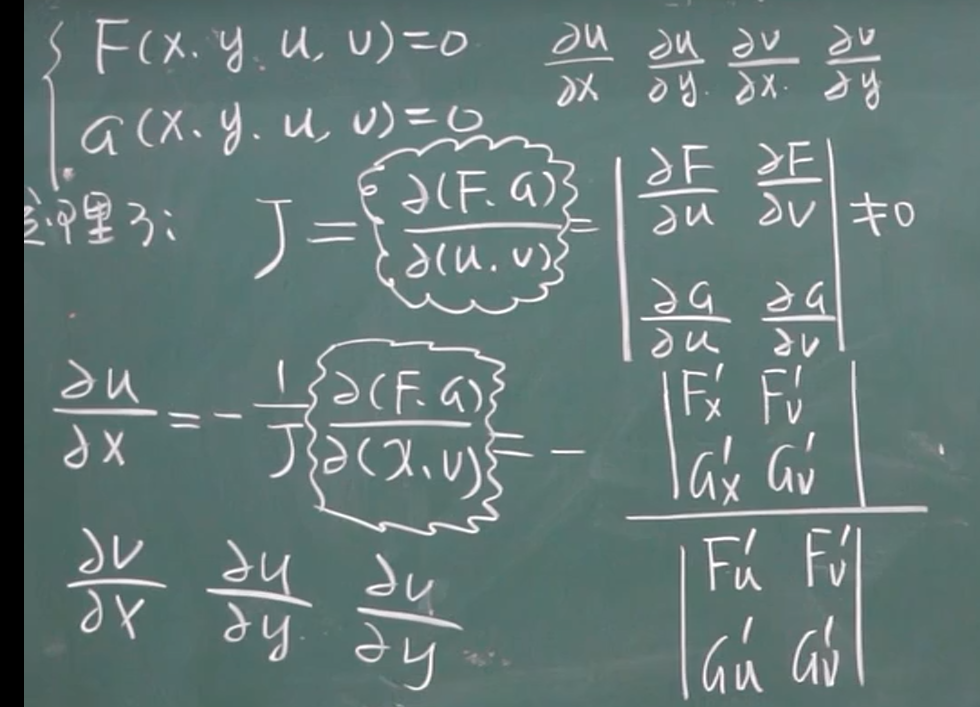
【九-11】一元向量值函数及其导数
一元:一个变量--t
向量:函数是由向量组成的

极限 -- 类似函数的定义
对应的导数:
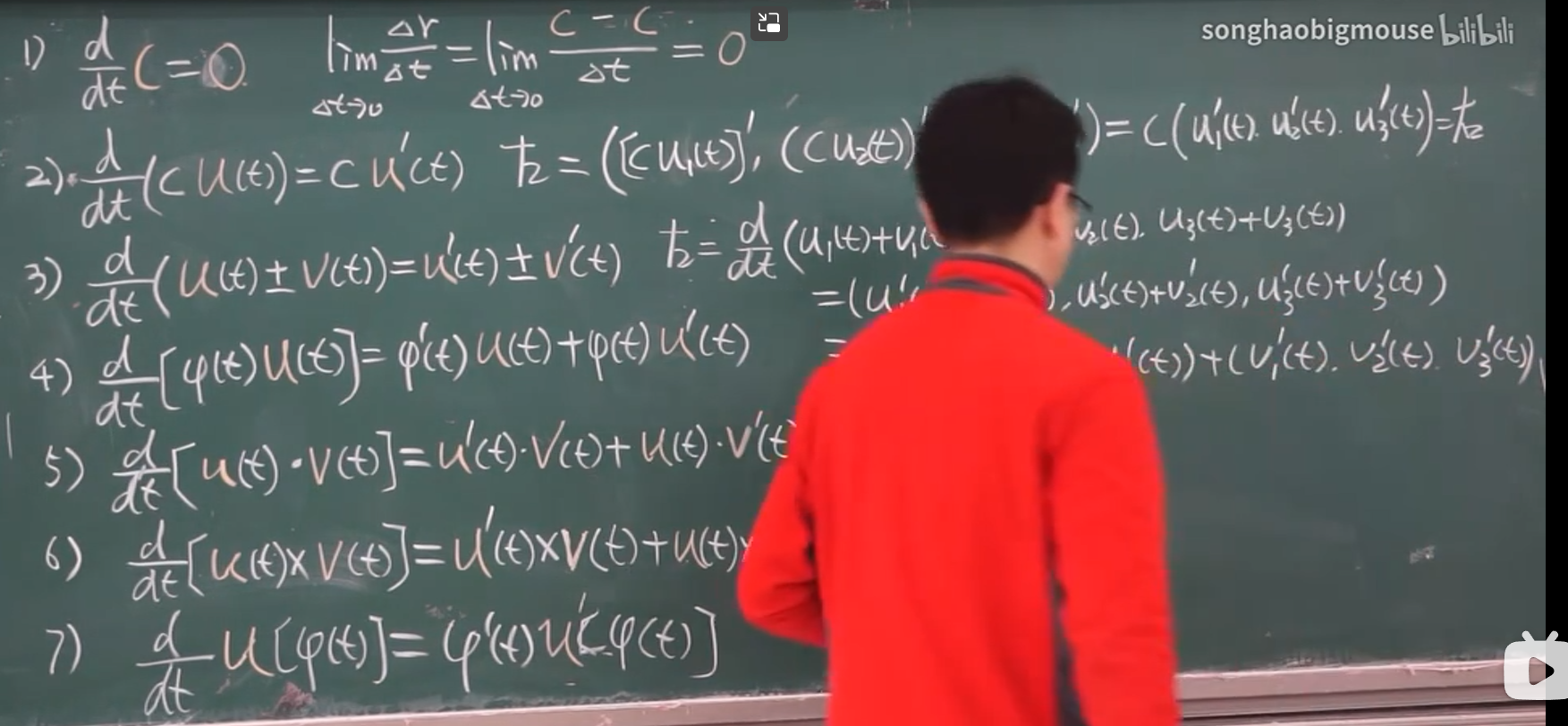
【九-12】空间曲线的切线与法平面
定义
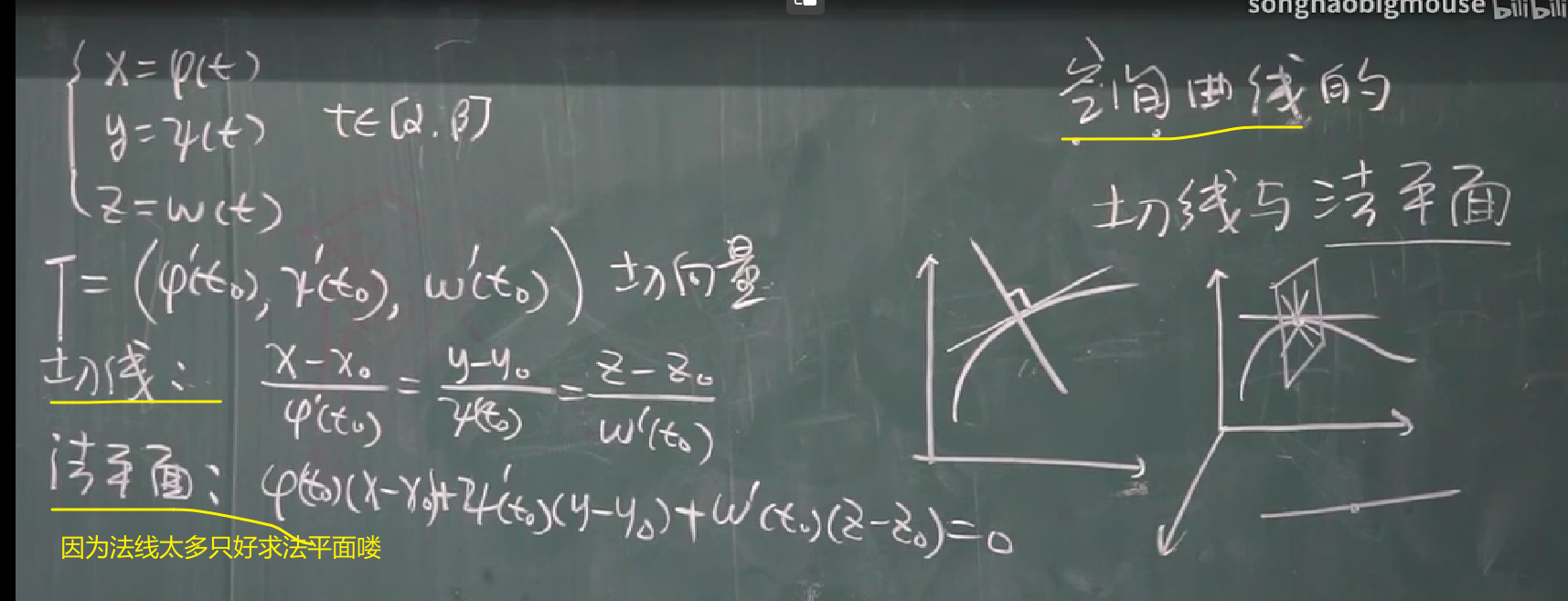
3种情况:
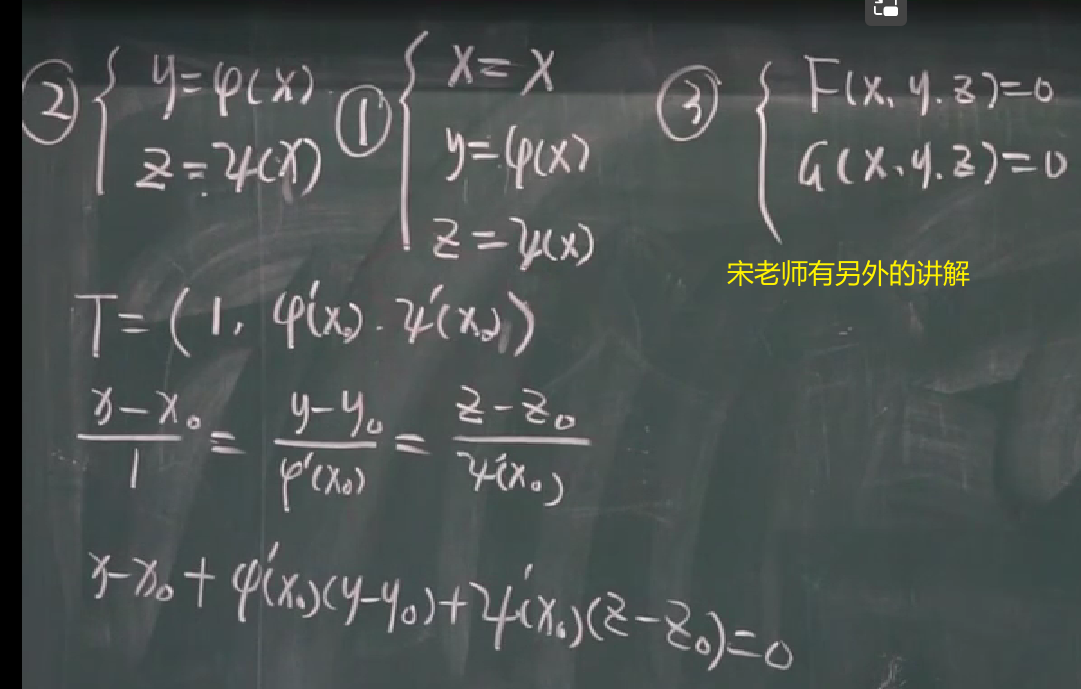
第3种解决方法:还是行列式

【九-13】空间曲面的切平面与法线
空间曲面的切线太多,形成了一个平面,所以求这个切平面
总共2种情况:这是一
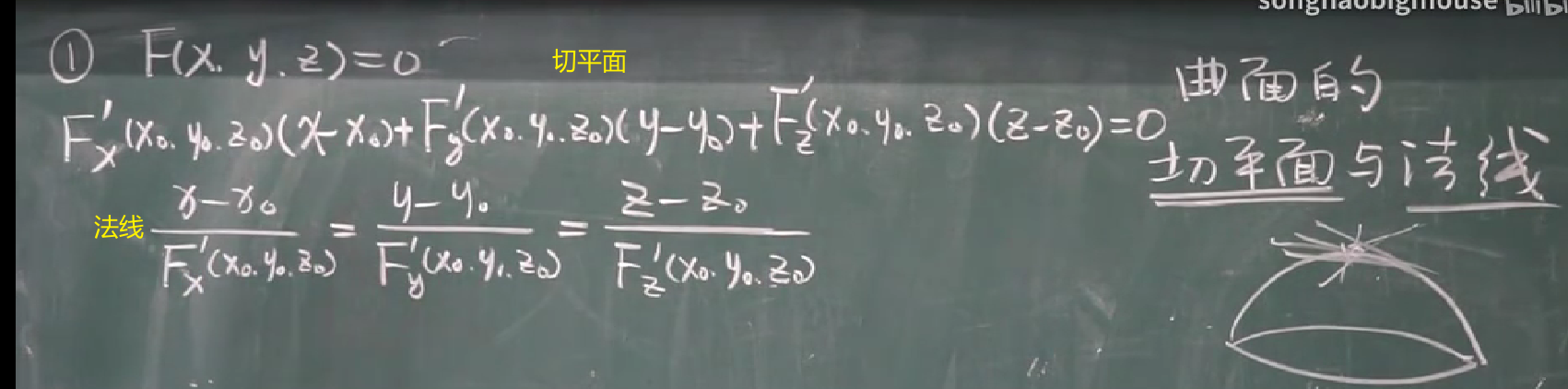
这是2:
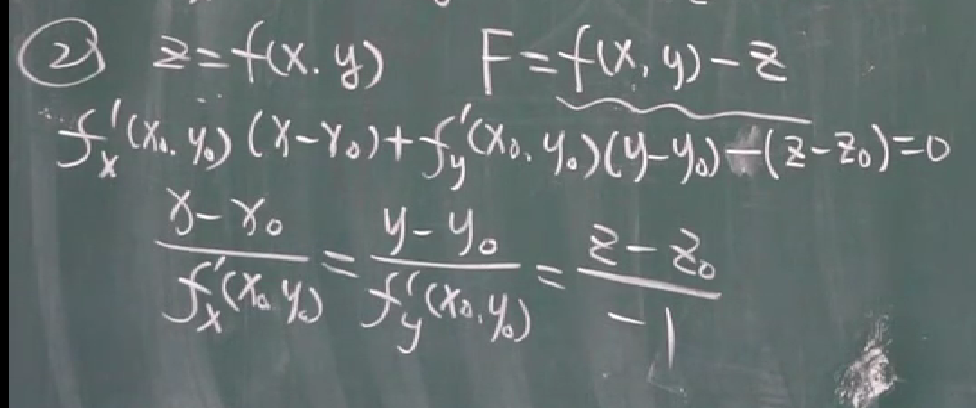
以上2节的内容容易分不清;但记住以下要点:乘法是面;除法是线
【九-14】方向导数
定义、、证明、例题:

多元函数的关于可微、可导、偏导数、方向导数存在的关系:多元函数中可微才是领先的

【九-15】梯度
梯度跟方向导数比较相似,但一个是数;一个(梯度)是向量:
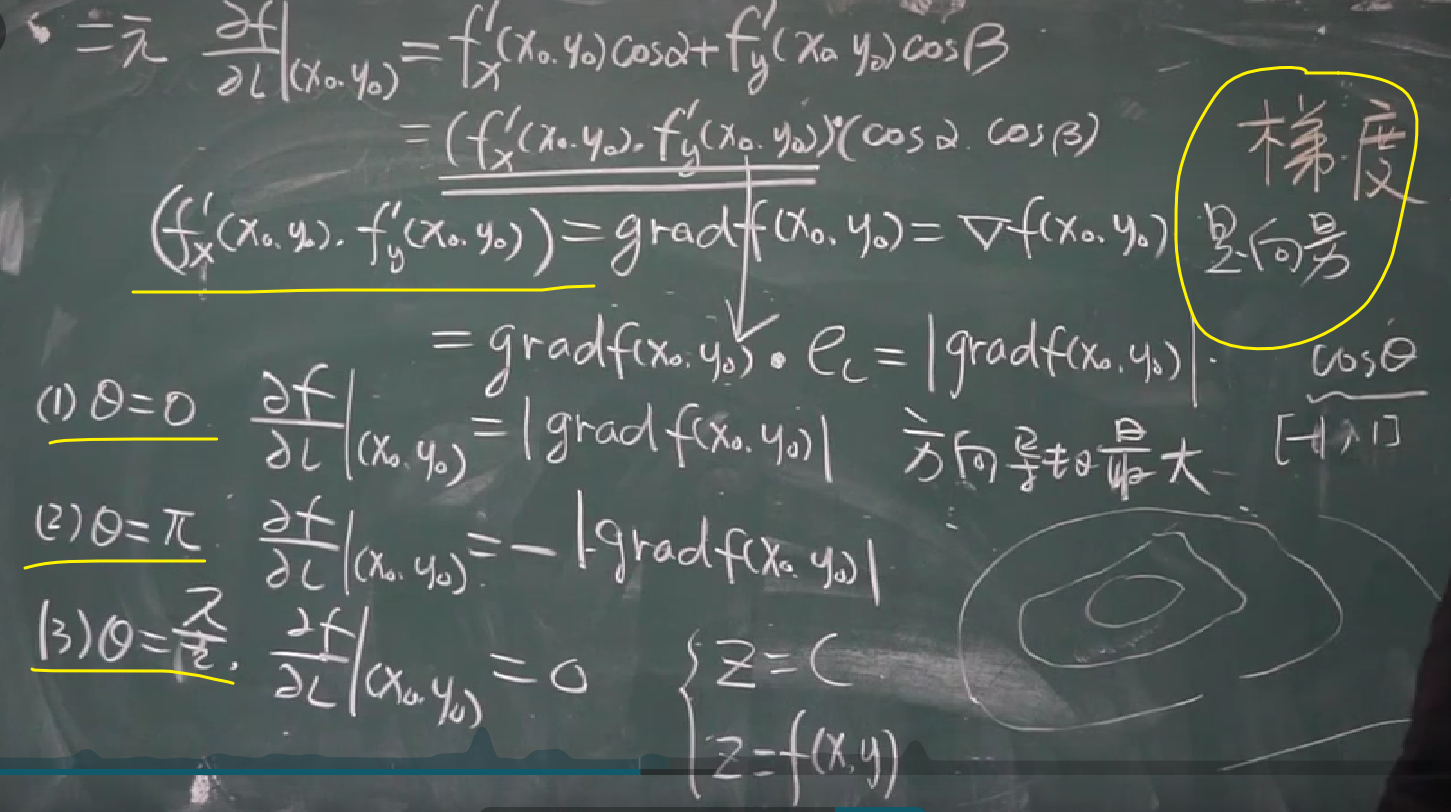
方向导数和梯度的关系图:方向导数就是沿着各个方法;梯度就是选择特定的几条方向导数
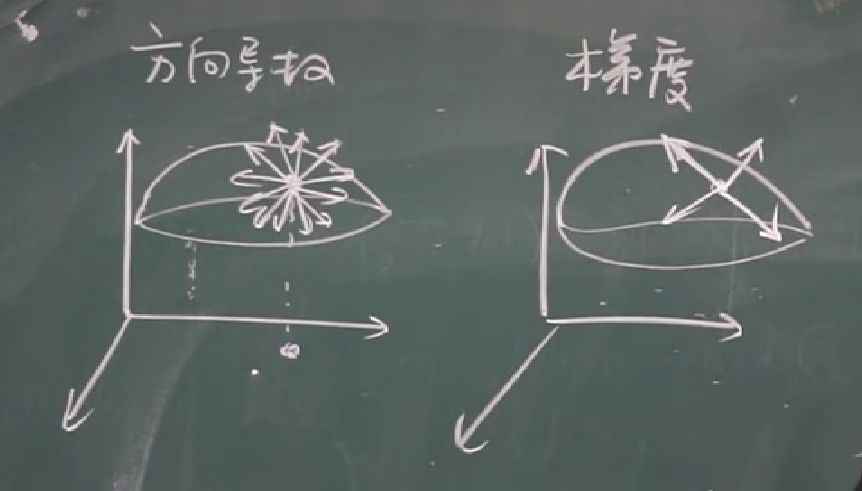
【九-16】方向导数和梯度的解释
梯度是二维向量:可以是三维向量在xoy平面上的投影
【九-17】梯度(例题#1)
分类讨论了3种情况:
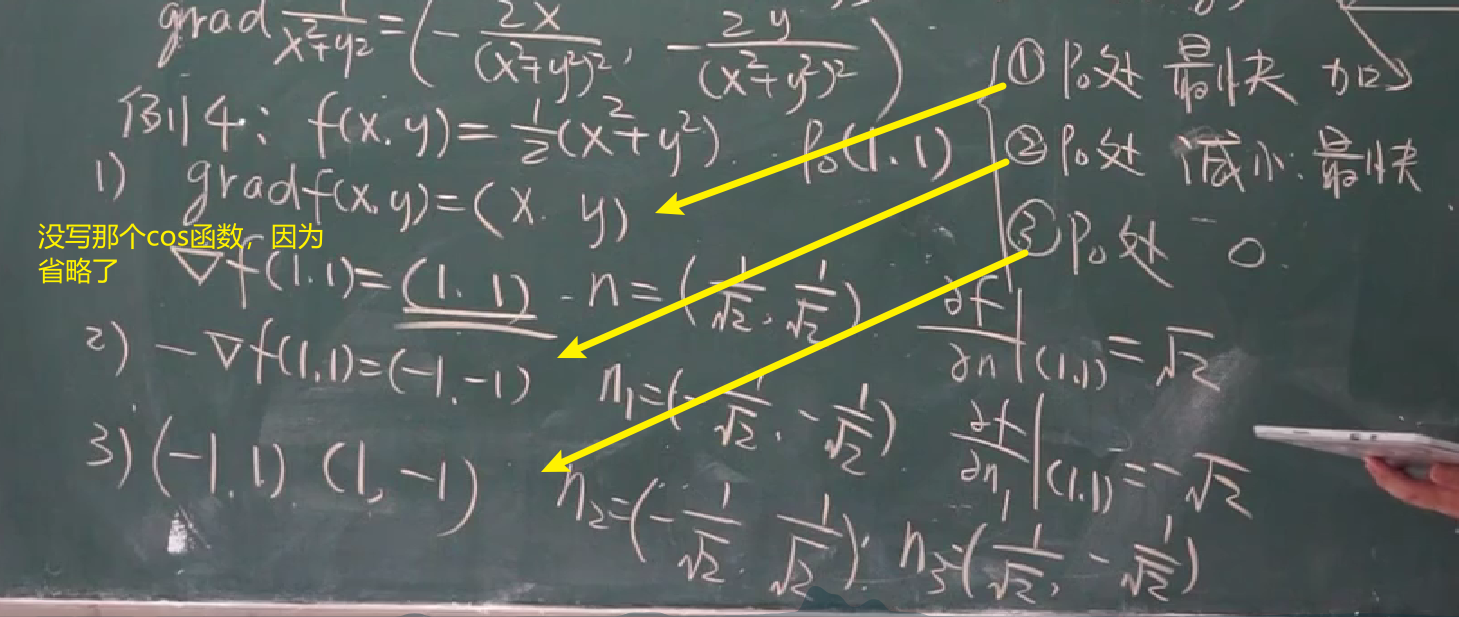
【九-18】梯度(例题#2)
【九-19】多元函数的极值
求二元函数的驻点、极值点:
先求一阶导得出可能的4个驻点;然后一次求每个驻点的二阶导数,利用AC-B^2的关系
判断是否是极值的3种情况
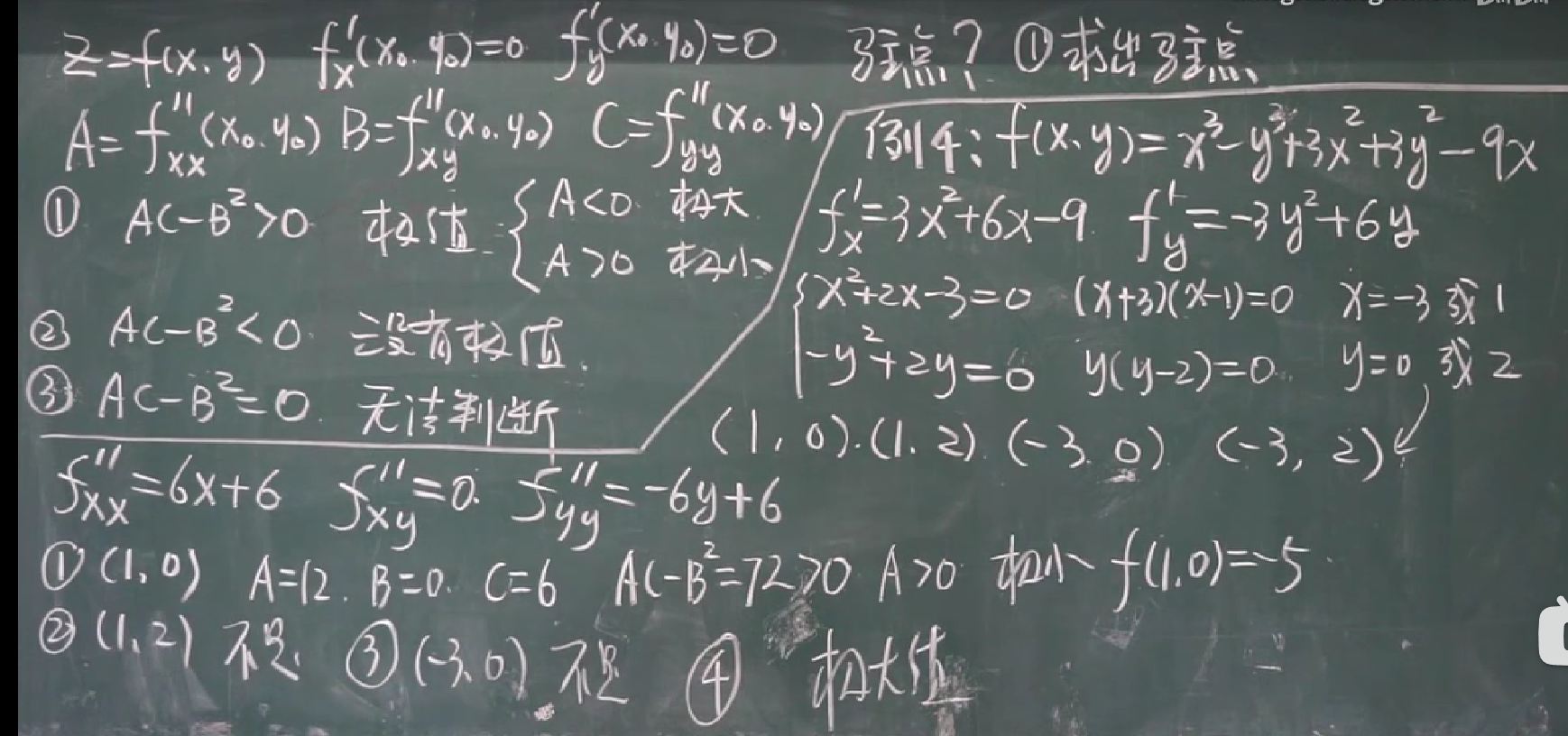
【九-20】数量场向量场
若向量场F(M)是某个数量函数f(M)的梯度,则f(M)是F(M)的一个势函数,F(M)为势场,故f(m)产生的梯度grad f(m)是一个势场 <--类比电场与电势的关系
【九-21】多元函数的最值
最值一般存在以下几类:驻点;片刀不存在点;定义域端点

【九-22】条件极值 拉格朗日乘数法(理论讲解)
反正就是列出方程,然后求解--考验的就是计算能力

【九-23】极值例题
既可用拉格朗日乘数法,也可转变成仅关于x,y的函数

【十-1】二重积分的定义
就是求曲顶柱体的体积

【十-2】二重积分的性质
前5个性质:
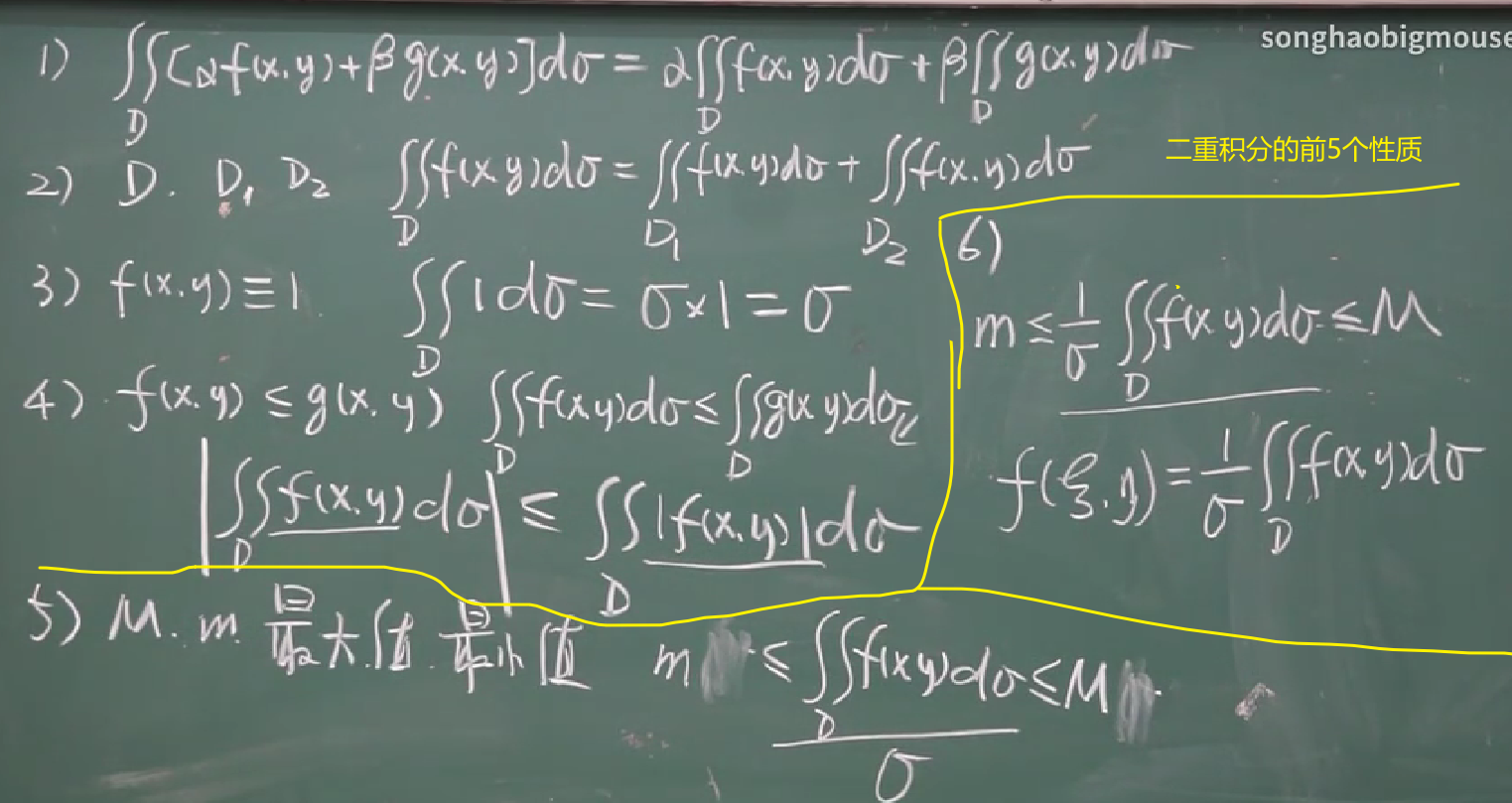
【十-3】二重积分的计算(直角坐标系)
- 先y后对x的积分:经常用,比较习惯将Y看做x的函数

- 先x后对y的积分
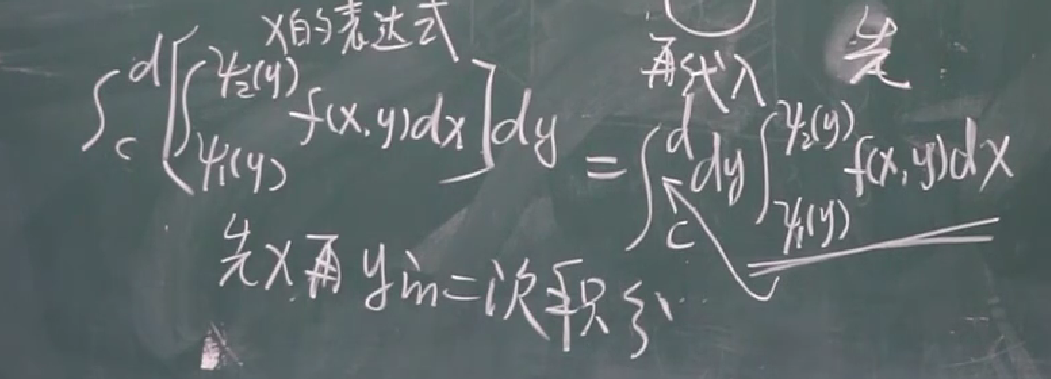
常见的积分区域:长方形

【十-5】极坐标介绍
介绍一般类型的极坐标公式

【十-6】二重积分(极坐标)
极坐标的公式:一般情况下都是先对角度积分,然后对P(肉)积分,
现在没遇到变换先后顺序的
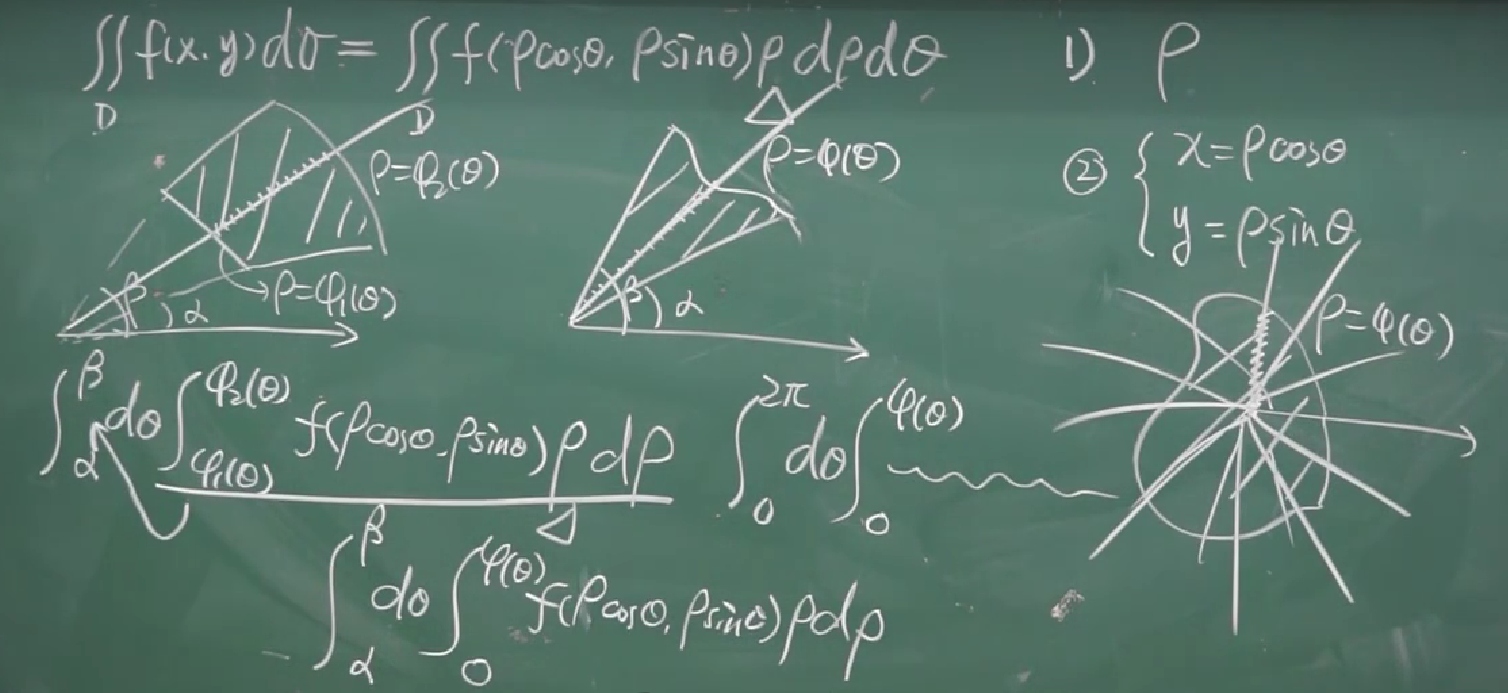
易错点:极坐标二重积分很容易少了个P(肉);
如何纠错:一般情况下,少了个P很难积分,所以那时应该想起宋老师的提示--别少了P(肉)
一个难以正常方法求出来的积分:必须记住的

【十-7】极坐标例题
一个简单的例题
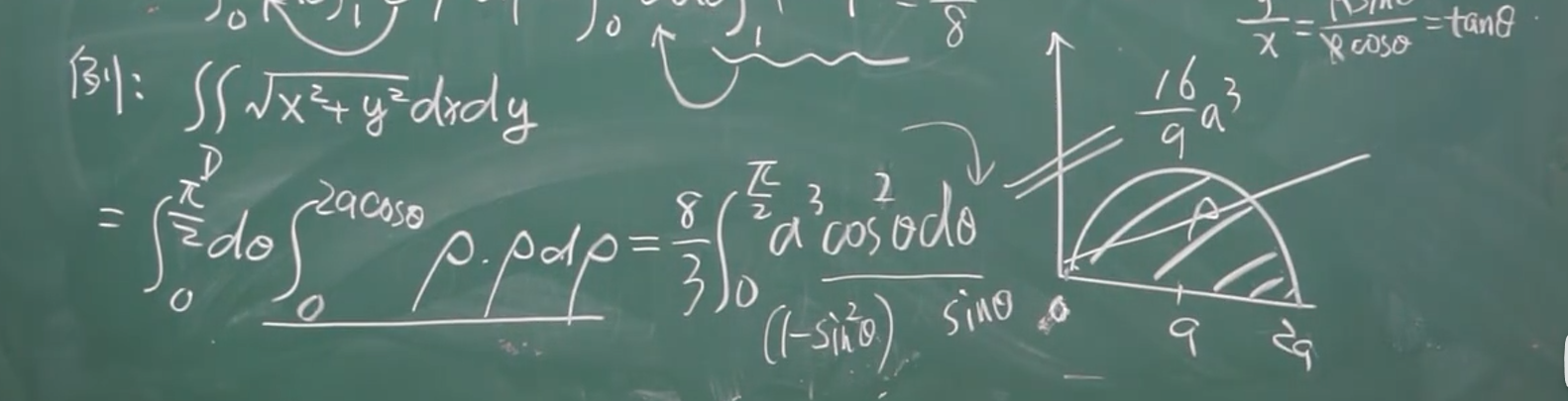
【十-8】二重积分的换元法
有点奇怪:之前的课程中从未看过
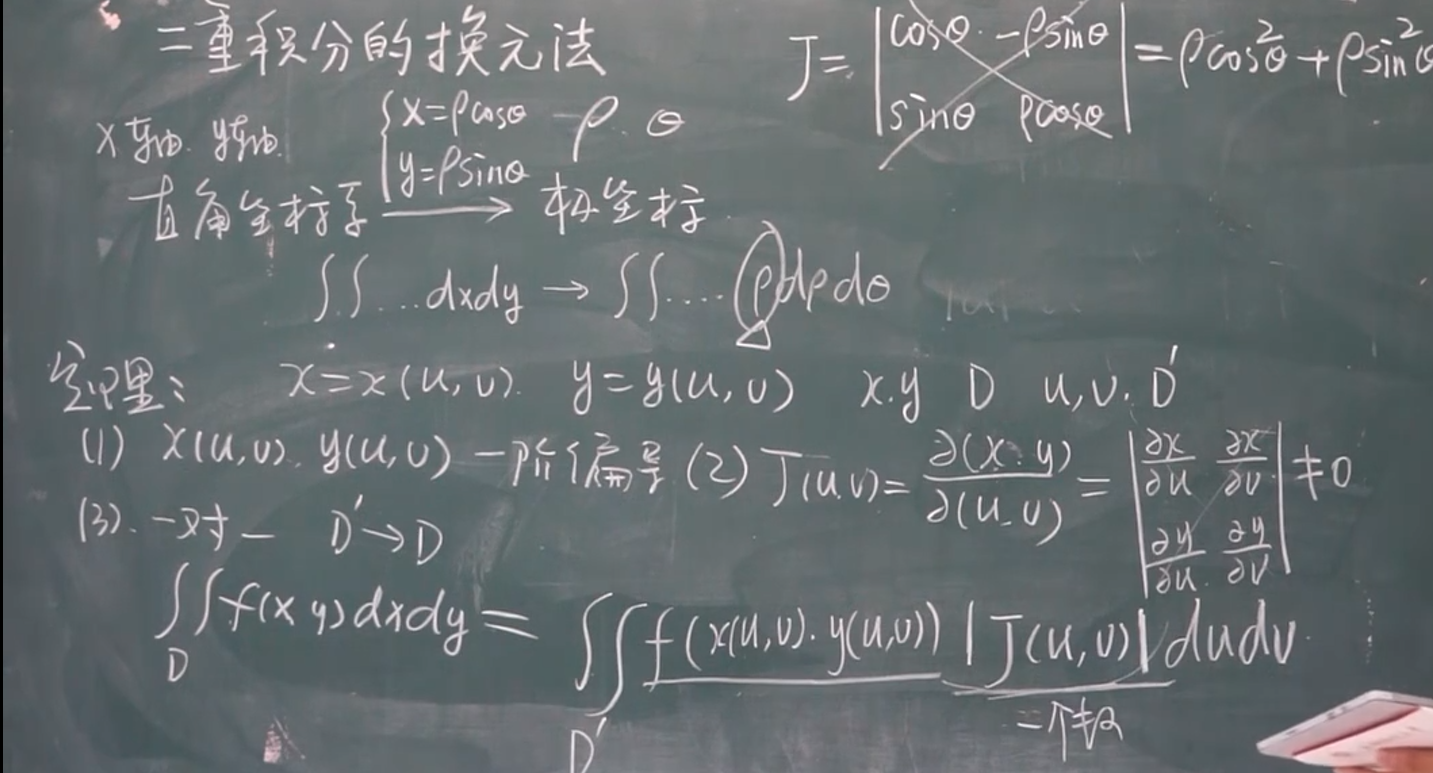
完整版本:不需要记太多
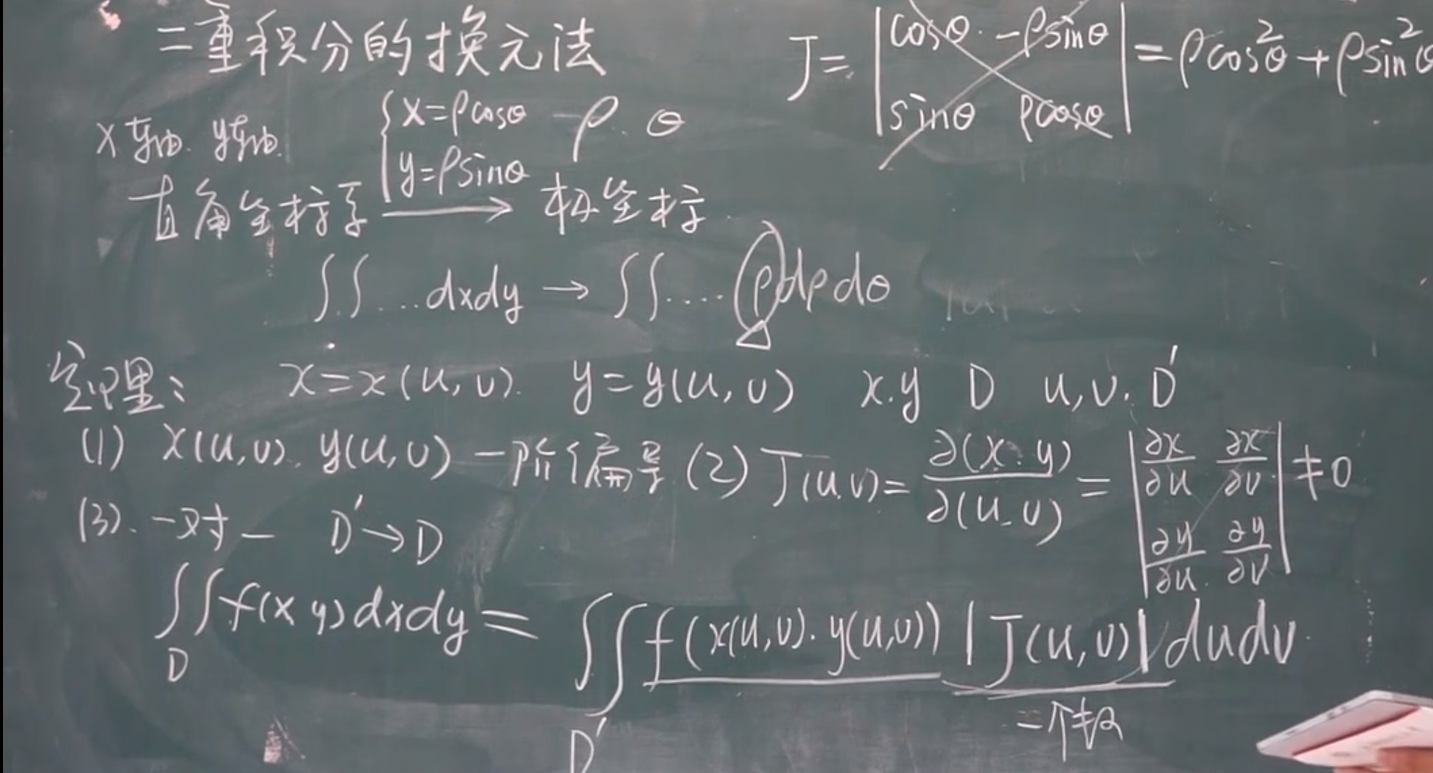
简略版本:
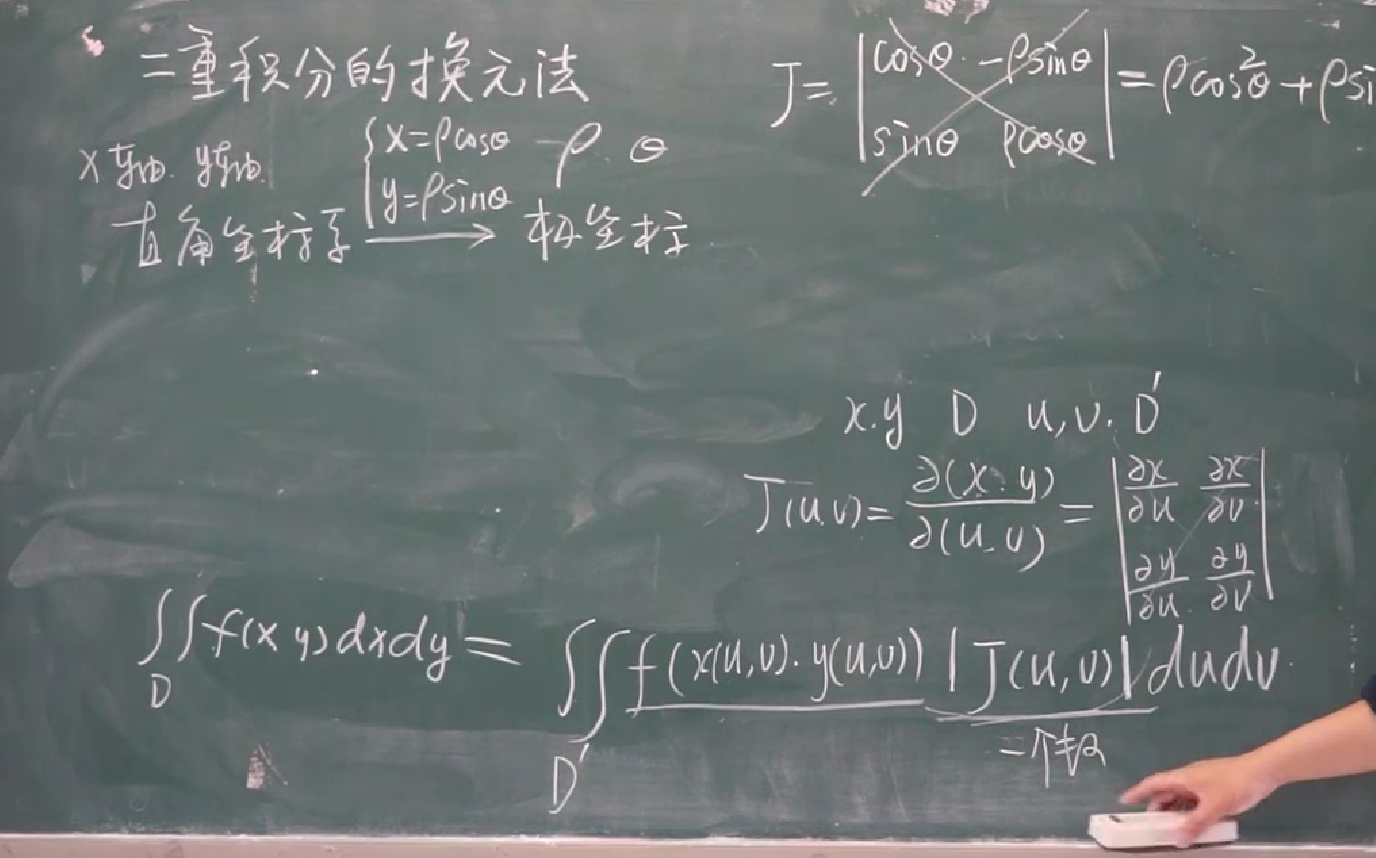
【十-9】三重积分的定义
【十-10】密度均匀&&不均匀的理解
【十-11】三重积分的计算(直角坐标系)
【十-12】例2
【十-13】柱面坐标
二重积分:
-
奇偶性:先找到被积函数中的奇函数(关于x,y,或许并没有),然后看积分区域是否满足奇函数,如果满足,那就是0,不满足,那就正常计算喽
-
轮转对称性:使用的目的是为了互补,如果使用更麻烦,不如不用

性质如下:

-
形心公式(有局限性:只能对被积函数为x或y进行计算,但遇到还是需要用的),例题如下:

-
易错点:x或y型区域:画那条垂直线时,先交的函数为下线,后交的为上线,这点易错! 其实这条线是个箭头,有顺序的。
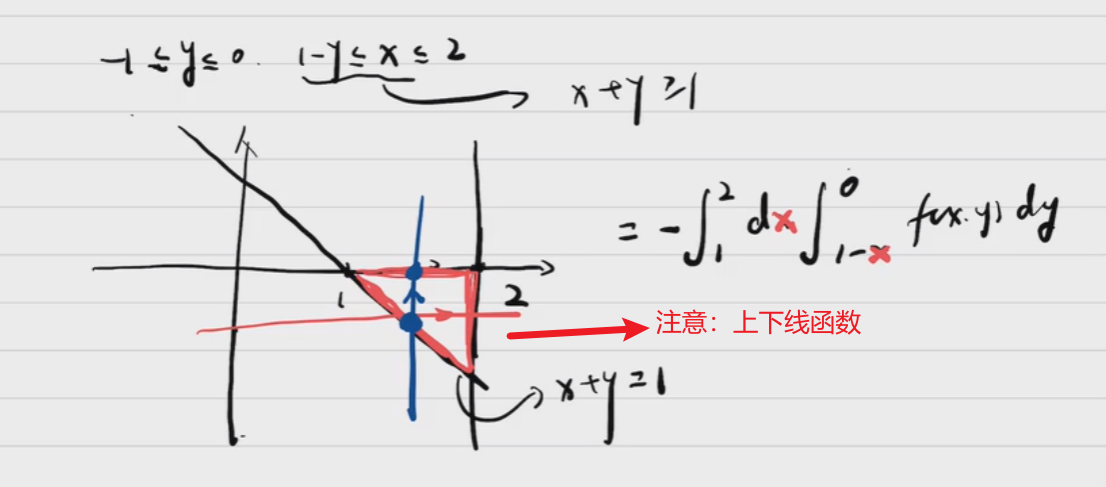
-
二重积分的第一步是确定被积区域,然后化简被积函数。
-
可以用直角坐标计算,也可以用极坐标计算(当出现x2+y2,,即圆的时候用)

-
积分区域关于原点对称:

三重积分的运算:还是做的题目少啊
- 直角坐标系:
先一后二:

先二后一:
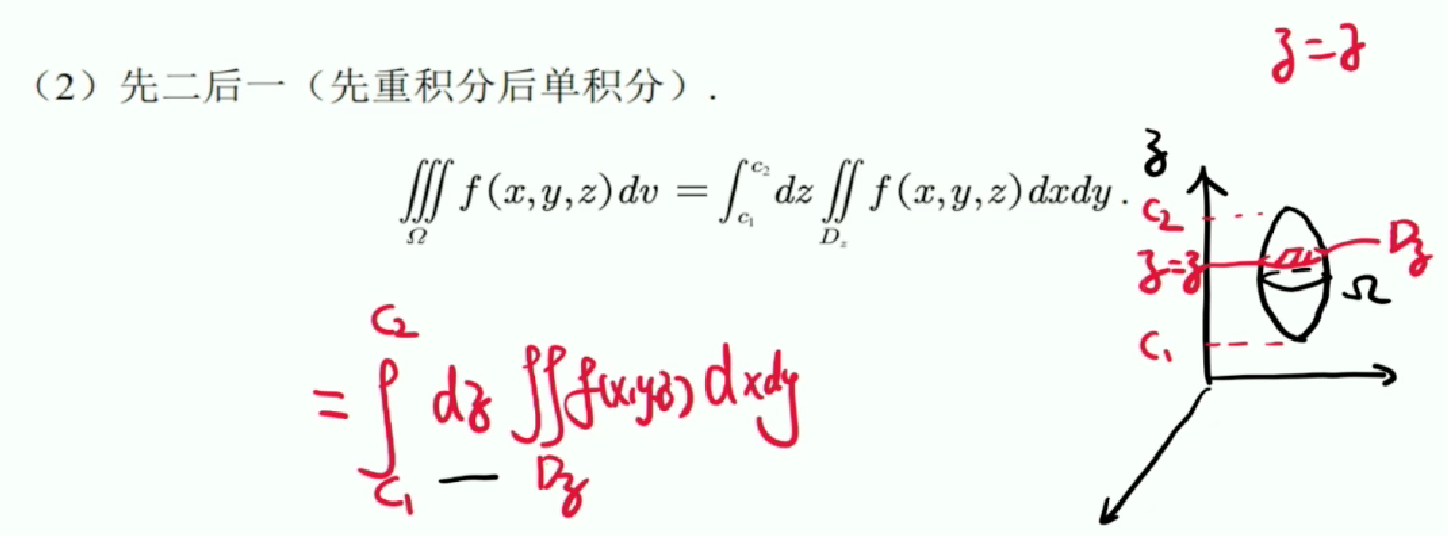
何时使用先二后一:从被积函数和被积区域

- 柱坐标
柱坐标与直角坐标系的关系:

公式:
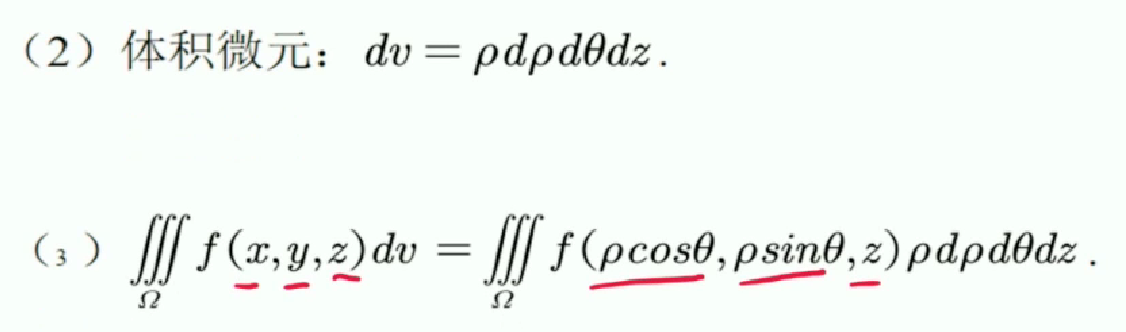
何时使用柱坐标:从被积函数和被积区域
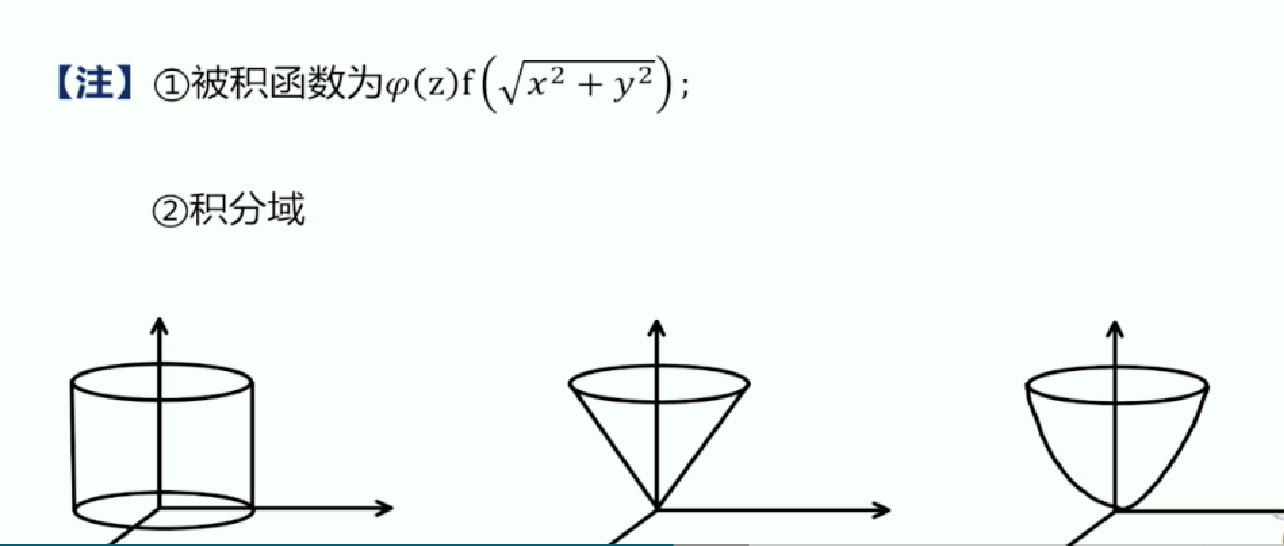
也有先一后二、先二后一:


- 对坐标的曲线积分:
性质:
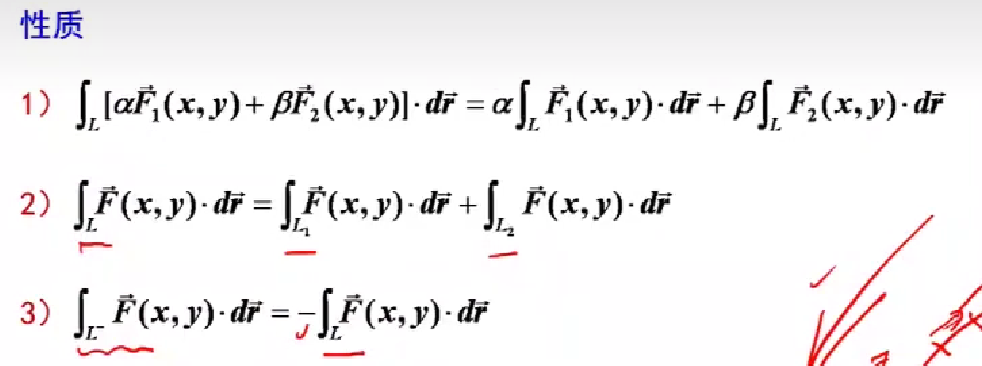
计算方法:分为参数方程和直角坐标方程

何时使用:跟二重积分一样
例题如下:

两类曲线积分的关系:不是多懂

- 对坐标的曲面积分:
对曲面的侧的分类:
前后;左右;上下;分别对于x,y,z轴