一、重要性
1.1 领域意义
群论是数学的一个分支,主要研究代数结构中的群、环、域等。尽管它看似抽象,但在编程领域,群论有着广泛的应用和深刻的意义。
- 算法设计与优化:群论在算法设计中发挥着重要作用。例如,在密码学中,群论被用于设计安全的加密算法,如椭圆曲线密码学,它依赖于椭圆曲线上的群结构;在图论和组合优化问题中,群论可以帮助识别和利用问题的对称性,从而简化算法或提高算法效率。
- 数据结构:群论的思想可以应用于数据结构的设计和分析。例如,在群论中,集合的运算和性质可以被用来优化数据结构的操作,如并查集等。群论还可以帮助理解数据结构中的复杂关系,如置换群在排列问题中的应用。
- 编程语言的语义:群论在编程语言的语义分析中也有应用。例如,类型系统可以看作是一种代数结构,其中的类型运算可以类比为群论中的运算。群论还可以用于研究编程语言的语法和语义之间的关系,以及语言之间的转换和等价性。
- 并发与分布式计算:在并发和分布式计算中,群论可以用于描述和分析进程或节点之间的通信和协作模式。通过群论的方法,可以设计出更高效、更可靠的并发算法和分布式系统。
- 软件工程与代码优化:在软件工程领域,群论可以用于分析代码的结构和性质,如代码的对称性、重复性和可重用性。通过群论的方法,可以识别出代码中的冗余部分,并进行优化和重构,以提高代码的质量和可维护性。
1.2 实践体会
最直接的就是「类型系统」的设计,借助群论中「封闭性」、「幺元和逆元」、「结合律」性质能够比较好地知道自己去Review一个功能涉及的各个数据结构,以及数据结构的交互逻辑是否完备、鲁邦。
- 数据结构,即为群中的元素
- 交互逻辑,即为群中的“运算”,只是这种运算比较复杂而已
二、数学概念
2.1 什么是群?
群(Group),本质是一堆“元素”的集合和一个运算操作。
元素它可以是任何数或者数学对象,运算可以加法、乘法或者任何其他复杂的操作。
它起源于对方程解析解的探索,由伽罗瓦为了解决特定数学问题而创造。群的定义可以概括为一个非空集合G以及在该集合上定义的一个二元运算“*”(通常称为乘法,但也可以是其他任何运算,只要满足群的定义)
2.2 有什么性质?
只要满足如下4条定义即可:
① 封闭性-Closure
即群里任意两个元素相“运算”后,结果也一定在群里。
a * b = c其中 a,b,c ∈ 集合G, * 为“运算操作”
- 这一点非常厉害,它抽象了很多数学分支领域的相似性。这也是为什么群论能够「概括绝大部分的数学对象」的原因。
- 群论所描写的数学对象是一个「封闭的数学系统」,故称之为“封闭性”
② 结合律-Associativity
即群里三个元素,无论是先算前面的 a * b,还是后面的b * c,结果都是一样。
(a * b) * c = a * (b * c)其中 a,b,c ∈ 集合G,* 为“运算操作”
- 意味着,在群论里面,左结合和右结合是没有差别的
- 如果群中的任意两个元素a和b,都有ab=ba,则称G为阿贝尔群(Abelian group)或交换群
③ 单位元-Neutral
即每个群里都包含唯一一个元素 e,当它与其他元素相“运算”时,结果还是那个元素。
a * e = a = e * a其中 a,e ∈ 集合G,* 为“运算操作”
- Neutral 直译过来是“中性元”,在中文里更常叫为“单位元”或者“幺元”
- 对于自然数而言,加法的单位元是“0”,乘法的单位元是“1”。这里的「加法、乘法」即是“运算”,「0, 1」即是群里的元素。因为“单位元”本质也是群里的元素。
④ 逆元-Inverse
即群里每个的元素a,都有唯一对应的“逆元” \(a^{-1}\),当它们进行运算时,结果是单位元 e
a * a^-1 = e其中 a,e ∈ 集合G,* 为“运算操作”
- 对于
a * b * c * d若想反向消解,则依次与它们的逆元做运算即可,即a * b * c * d * d^-1 * c^-1 * b^-1 * a^-1 = e - 对于
a*a*a*a = a^4,其逆元是a^-4
一些重要的思考题
Q:一个群里的「单位元」为什么是唯一的?不能有2个「单位元」吗?
# 证明过程根据单位元性质:a * e = a = e * a
假设一个群里有2个单位元 e1 和 e2,我们利用 e1 * e2 推导下二者关系:
① 参考 a * e = a 进行代入得:e1 * e2 = e1
② 参考 e * a = a 进行代入得:e1 * e2 = e2
③ 综合上述过程得: e1 = e1 * e2 = e2, 即 e1 = e2 得证唯一性
Q:一个群里的「逆元」为什么是唯一的?不能有2个「逆元」吗?
# 证明过程根据逆元性质:a * a^-1 = e,则 a^-1 * (a^-1)^-1 = e
① 先证明「a逆元的逆元等于a」a * a^-1 * (a^-1)^-1 = e * (a^-1)^-1 = (a^-1)^-1a * a^-1 * (a^-1)^-1 = a * e = a
② 证明逆元也满足「左消」a * a^-1 = e = (a^-1)^-1 * a^-1 即代入①结论,很明显得证
③ 证明逆元的唯一性,假设 a2^-1 也是 a 的逆元a * a^-1 = e 等式两边同时左乘 a2^-1a2^-1 * a * a^-1 = a2^-1 * ee * a^-1 = a2^-1a^-1 = a2^-1 得证逆元唯一性
- 对于群,我们从4个基本定义推导出了额外4个性质:
a. 逆元满足左消:a^-1 * a = e
b. 逆元的逆元等于本身:(a^-1)^-1 = a
c. 逆元的唯一性
d. 平方的逆元等于逆元的平方:(a^2)^-1 = (a^-1)^2 - 注意:群关于单位元的定义要求 e既要满足右消、也要满足左消,这一点要Keep in Mind.
a. 但其实群最弱定义可只要求单位元满足右消,左消可以证明出来(留个作业)
从上面可知,在数学大厦里类似负负得正、倒数的倒数是原数都只是「逆元的逆元是原元素」这一底层原理的具体例子而已,意味着群论默默地统治着所有的数学系统!
2.3 常见群有哪些?
2.3.1 整数集
整数集(记为Z),搭配“加法”运算,则就构成了一个群。
+
... -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 ...①封闭性:-2 + 1 = -1 ∈ Z ✅
②结合律:(1+2)+3 = 1+(2+3) ✅
③单位元:0 + -3 = -3, 4 + 0 = 4 ✅
④逆 元:-5 + 5 = 0, 2 + -2 = 0 ✅
整数集(记为Z),搭配“乘法”运算,就无法构成一个群。对照群的4个定义可知不满足「逆元」:4 * 1/4 = 1 其中1是单位元(在群里),但1/4不在群里
2.3.2 有理数集
思考题:有理数集(记为Q,包含正负整数、分数),搭配“乘法”运算,是否一个群呢?
x
... -4/5 -3/4 -1/3 -1/2 0 1/2 2/3 1/4 2/5 ...①封闭性:1/2 x 3/5 = 3/10 ∈ Z ✅
②结合律:(1x2)x3 = 1x(2x3) ✅
③单位元:1 x -3 = -3, 4 x 1 = 4 ✅
④逆 元:-5 x -1/5 = 1, 0 x 1/0 = ? ❌(0 没有倒数)
答案:不构成。因为 0 x 1/0 是一个特殊的情况。如果把0从集合Q中排除,则就构成一个群。
为了表示上的简洁性,上面两个群我们可以分别记为 \(Z^{+}\)、\(Q^{×}\) 。注意后者是不包含0的。
2.3.3 循环群 \(Z_n\)
\(Z_n\) 表示所有的循环群,n是一个占位符,可以是任意整数,此处我们以 n = 6 时的 \(Z_6\) 群举例:
+
0 1 2 3 4 5①封闭性:1 + 2 = 3 ∈ Z,4 + 5 = 3 ✅
②结合律:(1+2)+3 = 1+(2+3) ✅
③单位元:0 + 3 = 3, 4 + 0 = 4 ✅
④逆 元:2 + 4 = 0, 5 + 1 = 0 ✅
- 「循环」的含义是:0+1 = 1,1+1 = 2,... 4+1 = 5, 5+1=0
- 对于正六变形,分别按照一个方向旋转0°、60°、120°、180°、240°、300°,产生了不同的“位置状态”。旋转360°(即300°+60°)效果等同于旋转0°,即产生了「循环效果」。
a. 此时群也是「阿贝尔群」,因为满足交换律,即「60°+120°」 = 「120°+60°」
b. 如果把“运算”操作由「旋转」,改为「旋转+反转」,则就不满足交换律了,也就不是「阿贝尔群」了(但依然是一个群)。
2.4 群的阶
群里包含的元素的个数,即为群的阶。
\(|Z^{+}| = |Q^{×}| = \infin\),即前面介绍的两个群的阶都是无穷。
\(|Z_{6}| = 6\)
2.5 用群来研究群
2.5.1 子群的概念
一个子群,是指从一个群中抽出一部分元素,并且恰好也构成了一个群。
- 「偶数」就是「整数」的子群;但「奇数」就无法构成一个子群了
- \([0, 3, 6]\)是\(Z_9\)的一个循环子群
由“旋转”构成的子群可以描述为“60°旋转”的倍数;{0,3,6} 循环子群可以描述为“3的倍数”。普遍地,对于任意一个元素 a,所谓“a生成的子群”,就定义为 “a的倍数”,记为 <a>
<a> = {a, a^2, a^3, a^4, ....}有限阶的生成子群一定会包含单位元(如下图,记住仅针对有限阶)
①单位元:a^8 = e ✅
②逆元:a * a*7 = a^8 = e, a^6 * a^7 = a^13 = a^5 * a^8 = a^5 ✅

- 上述仅针对「有限阶」的生成子群,对于无限阶失效。
a. 试着“正偶数构成的子群”视为“2的生成子群”?❌(少了逆元,和单位元)
思考题:如何在无限群里找到一个元素,使得我们在生成这个元素的子群时,不用考虑它的单位元和逆元?
2.6 群与子群的对称性
群与它的子群是高度对称的。即但我们把子群「复制平移」时,它就可以覆盖整一个群。
2.6.1 整数群与偶数子群
由前术可知,整数群\(Z^{+}\)存在一个偶数子群\(<2>^{+}\),也有奇数子集。
- 奇数子集并不一定构成群,但它可以通过由偶数子群通过复制平移得到(只需要将所有群中元素+1即可)
- 由一个子群平移而来的东西,称之为「陪集」,即coset。
a. 上述奇数子集,数学上记为\(1+<2>^{+}\) - 偶数子群平移偶数距离后是它自身,因此一个群也可以看作是自己的陪集。
a. 即$2+<2>^{+} = <2>^{+} $
2.6.2 「子群+陪集」可等分一个群
证明:子群所衍生出来的陪集,可以整齐地将整个群切分为一样的大小。

1. 基本事实①:“陪集”肯定可以覆盖整个群
因为不论你想覆盖哪一个元素 x,可以简单粗暴地将子群平移到这个元素。因为 x * e = x

2. 基本事实②:所有的“陪集”都是一样大小的,因为平移不可能凭空多出元素。
a. 但需要证明「不会减少元素」,即平移时子群到陪集出现了多对一

# 证明不会减少元素假设从子群平移到陪集时,存在 y * c = y * b 导致了元素减少
根据逆元操作,我们可以把此陪集的元素都左乘逆元 y^-1,再平移回去,即
y^-1 * y * c = y^-1 * y * be * c = e * bc = b // ->>> b,c属于同一个群,群内是不存在重复元素的,与群定义违背
基于前面2个事实,如果我们要证明「子群所衍生出来的陪集,可以整齐地将整个群切分为一样的大小」,则只需证明「“陪集”之间不会相互重合」。

# 证明过程对于子群G = {e, a, b, c,..}, 对群内元素逐一平移 z “距离”, 则:
① 如果 z 是 群G内元素,则显然 z * {e, a, b, c, ...} ∈ G,因为群具有封闭性
② 如果 z 是 群G外的元素,那是否平移之后是否存在某个元素a满足 z * a ∈ G 呢?假设 z * a = b, 我们都右乘一个逆元 a^-1,即得:z * a * a^-1 = b * a^-1z = b * a^-1 等号右边 b 和 a^-1 都在群G中,根据封闭性得知,结果z也应该子群G里,这与②的假设违背故若 z 是群G外元素,则平移之后陪集与G不重合。
因此我们推导出了一个二分论断:一个陪集要么与之前子群完全不重合,要么就是子群本身。相似地,此二分论断在陪集与陪集之间也是成立的。
综上,我们证明了:“子群所衍生出来的陪集,可以整齐地将整个群切分为一样的大小”。
2.6.3 拉格朗日定理
对于有限群,上述这种对称性完全适用!
拉格朗日定理:对于一个群G和它的子群H,H的阶可以整除G的阶。即\(|H| divides |G|\)

+
0 1 2 3 4 5 -> |G| = 6子群:
0 2 4 -> |H| = 3即,6/3 = 2, 且不可能存在阶数为4或5的子群。
这个定理有什么用?对于一个阶数为“质数p”的群,意味着它的子群只能拥有1个或p个元素。
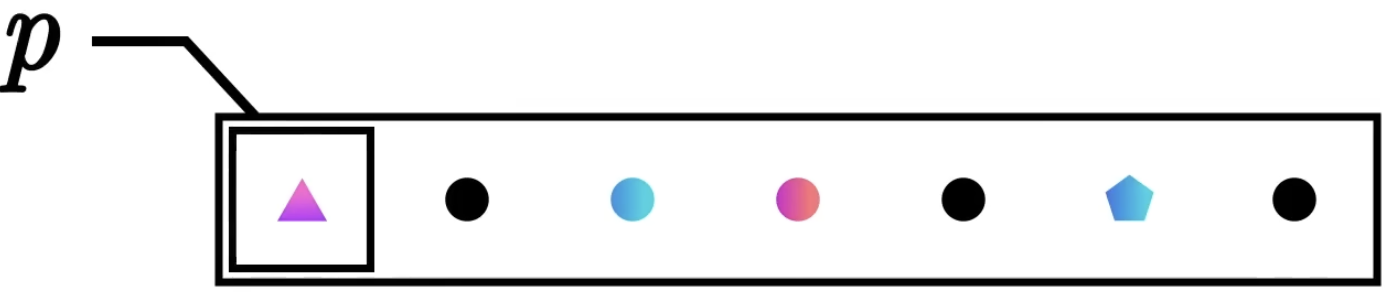
对于一个阶数为“质数p”的群,它一定是个循环群
参考资料:
- https://www.youtube.com/watch?v=KufsL2VgELo
- [双语字幕] 史上最好的群论入门_哔哩哔哩_bilibili