题目传送门
扫描线是一种求矩形面积并或周长并的好方法。
假设在一个平面上有几个矩形,要求它们共覆盖了多大的面积。由于矩形可能会有重叠的地方,所以最后要求的图形就是一个不规则的图形。
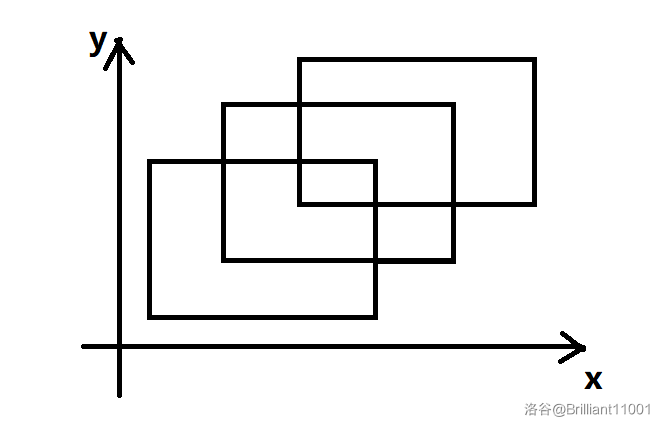
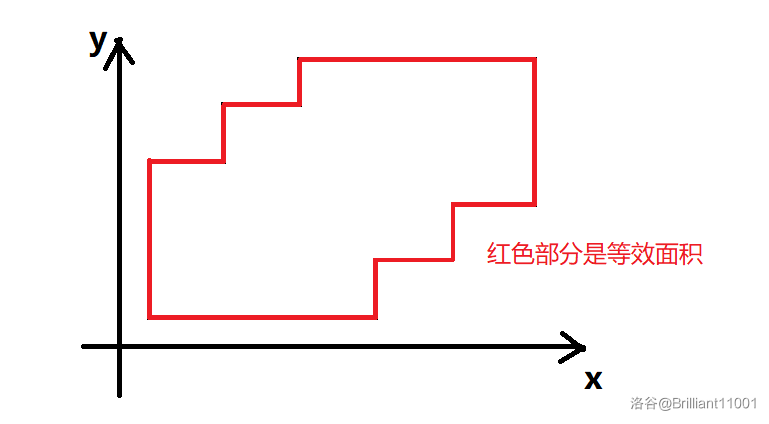
要求它的面积十分复杂,特别是在矩形数量很大时。为了解决这个问题,扫描线法应运而生。
想象一下,有一根看不见的直线从下到上扫过这个平面。在扫描的过程中,直线上的一些线段会被给定的矩形覆盖。如果我们将这些覆盖的线段长度进行积分,就可以得到矩形的面积之和。
如图所示:
图是我从 OI WiKi 上偷的。
这时候就有一个疑问了:这玩意儿和线段树有什么关系呢?
先别慌,我们慢慢分析。
由图可知:直线上被并集图形覆盖的长度只会在每个矩形的上下边界处发生变化。换言之,整个并集图形可以被分成 \(N \times 2\) 段,每一段在直线上覆盖的长度(记为 \(L\))是固定的,因此该段的面积就是 \(L\times\) 该段的宽度,各段面积之和即为所求。
为了快速计算出截线段长度,可以将横边赋上不同的权值,具体为:对于一个矩形,其下边权值为 \(1\),上边权值为 \(-1\)。
然后把所有的横边按照 \(y\) 坐标升序排序。这样,对于每个矩形,扫描线总是会先碰到下边,然后再碰到上边。那么就能保证扫描线所截的长度永远非负了。
我们维护一条扫描线,将这条线逐渐向上平移,遇到每一根横着的线就停下来,算算目前扫描线上被覆盖的长度和与上次停下相比走过了多少距离,两者相乘后累加到 ans 里。
然后再看目前遇到的这根线,如果是 \(+1\) 线就将它覆盖到扫描线上,否则就将它从扫描线中减去。
朴素的做法是维护一个数组 \(s\) 作为扫描线,用一个 \(len\) 维护目前扫描线上被覆盖的长度,\(s_{i}\) 表示扫描线上的这个坐标被覆盖了几次。
这样,每遇到一条 \(+1\) 线,就在 \(s\) 数组上进行朴素 \(+1\),反之 \(-1\),同时更新 \(len\)。
这样做的时间复杂度最坏为 \(O(n^2)\)。
考虑优化。
容易发现这个算法的瓶颈在于朴素的区间加和区间减,所以用线段树来维护。
建立一棵线段树,维护两个值:
-
该线段被覆盖的次数;
-
该线段被覆盖的长度。
那线段树该怎么建立?
细节一:
一般这种类型的题矩形的坐标要么就特别大,要么就可能是小数,这时候就需要进行离散化。一定要注意下标的转化!
值得注意,线段树中的叶子节点表示的区间 \([l, r]\) 其实不能直接用来表示元线段,因为 \(l = r\),表示的其实是长度为 \(0\) 的线段,所以我们需要对它进行一些调整。
考虑把线段树每个节点 \(u\) 对应的区间 \([l, r]\) 不变,改变区间和横边的映射关系,具体为:节点 \(u\) 对应 \((xs_{u}, xs_{u} + 1)\) 这条横边。
细节二:
虽然有区间修改操作,但是并不需要懒标记。
因为只有当该线段被覆盖的次数大于 \(0\) 时才会被用来更新答案,我们又只用询问根结点的值,所以只需要保证所有节点的父节点的信息是正确的,就能保证答案的正确性,而此时子结点的值就不需要用到了,所以不需要 \(\operatorname{pushdown}\)。
那为什么是正确的呢?
我们维护了两个值:\(cnt\) 和 \(len\),因为 \(+1\) 和 \(-1\) 操作必定是成对出现的,而且先 \(+1\) 再 \(-1\),所以 \(cnt\) 必定大于等于 \(0\),我们不妨对此进行分类论:
-
当 \(cnt = 0\) 时,这时长度就用它的两个儿子来计算,只需要在修改完后 \(\operatorname{pushup}\) 一遍就行了,这时候有没有 \(\operatorname{pushdown}\) 都没有关系。
-
当 \(cnt > 0\) 时,此区间完全被覆盖,则 \(len = r - l + 1\),这时再给这个区间加上一个数,若加完后 \(cnt > 0\),则完全没有影响,因为我们只统计 \(cnt\) 大于 \(0\) 的长度,所以长度还是 \(r - l + 1\);若加完后 \(cnt = 0\),则同上。
综上所述,不需要 \(\operatorname{pushdown}\) 操作。
\(\texttt{Code:}\)
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;const int N = 100010;
typedef long long ll;
struct Segment{int y, x1, x2;int val;bool operator <(const Segment &o) const {return y < o.y;}
}seg[N << 1];struct node{int l, r;//线段树的节点tr[u]表示的线段树Node区间[tr[u].l,tr[u].r]维护离散化后的区间 --> [y_l, y_r + 1]int cnt;int len;#define l(x) tr[x].l#define r(x) tr[x].r#define cnt(x) tr[x].cnt#define len(x) tr[x].len
}tr[N << 4];vector<int> xs;
int n;inline int ls(int p) {return p << 1;}
inline int rs(int p) {return p << 1 | 1;}int find(int x) { //返回x在vector中储存的下标 return lower_bound(xs.begin(), xs.end(), x) - xs.begin();
}void pushup(int p) {if(cnt(p)) len(p) = xs[r(p) + 1] - xs[l(p)]; //若全部覆盖,被覆盖的长度就是区间长度 else if(l(p) != r(p)) {// 如果tr[u].cnt等于0其实有两种情况:// 1. 完全覆盖. 这种情况由modify的第一个if进入. // 这时下面其实等价于把"由完整的l, r段贡献给len的部分清除掉", // 而留下其他可能存在的子区间段对len的贡献// 2. 不完全覆盖, 这种情况由modify的else最后一行进入. // 表示区间并不是完全被覆盖,可能有部分被覆盖,所以要通过儿子的信息来更新len(p) = len(ls(p)) + len(rs(p));}else len(p) = 0; //表示为叶子节点且该线段没被覆盖,为无用线段,长度变为0
}void build(int p, int l, int r) {l(p) = l, r(p) = r;if(l != r) {int mid = l + r >> 1;build(ls(p), l, mid);build(rs(p), mid + 1, r);}
}void modify(int p, int l, int r, int val) { //表示从线段树中l点到r点的出现次数 + valif(l <= l(p) && r >= r(p)) {cnt(p) += val;pushup(p); //更新该节点的lenreturn ;}int mid = l(p) + r(p) >> 1;if(l <= mid) modify(ls(p), l, r, val);if(r > mid) modify(rs(p), l, r, val);pushup(p);
}int main() {scanf("%d", &n);int x1, x2, y1, y2;for(int i = 0, j = 0; i < n; i++) {scanf("%d%d%d%d", &x1, &y1, &x2, &y2);seg[j++] = {y1, x1, x2, 1};seg[j++] = {y2, x1, x2, -1};xs.push_back(x1);xs.push_back(x2);}sort(seg, seg + n * 2); //将横着的线段按照y坐标从小到大排序 sort(xs.begin(), xs.end());xs.erase(unique(xs.begin(), xs.end()), xs.end()); //离散化去重 //离散化后纵坐标有2n个点, 2n-1个区间,构建线段树,线段树的节点维护这些区间tr[i] --> [y_i, y_i+1],所以线段树的节点个数与区间个数相同2n-1build(1, 0, xs.size() - 2); //共有xs.size() - 1个y点位,就会构成xs.size() - 2条线段 ll res = 0;for(int i = 0; i < n * 2; i++) {if(i > 0) res += 1ll * tr[1].len * (seg[i].y - seg[i - 1].y);modify(1, find(seg[i].x1), find(seg[i].x2) - 1, seg[i].val); //更新 //这里一定要把原区间 变换到 线段树表示的区间 //线段树的节点 维护 离散化后的区间:tr[u] --> [tr[u].l,tr[u].r] --> [xs_l, xs_r + 1]//原区间: seg[i].x1 ~ seg[i].x2//离散化后的区间: find(seg[i].x1) ~ find(seg[i].x2)//线段树中的区间: find(seg[i].x1) ~ find(seg[i].x2) - 1}printf("%lld\n", res);return 0;
}












