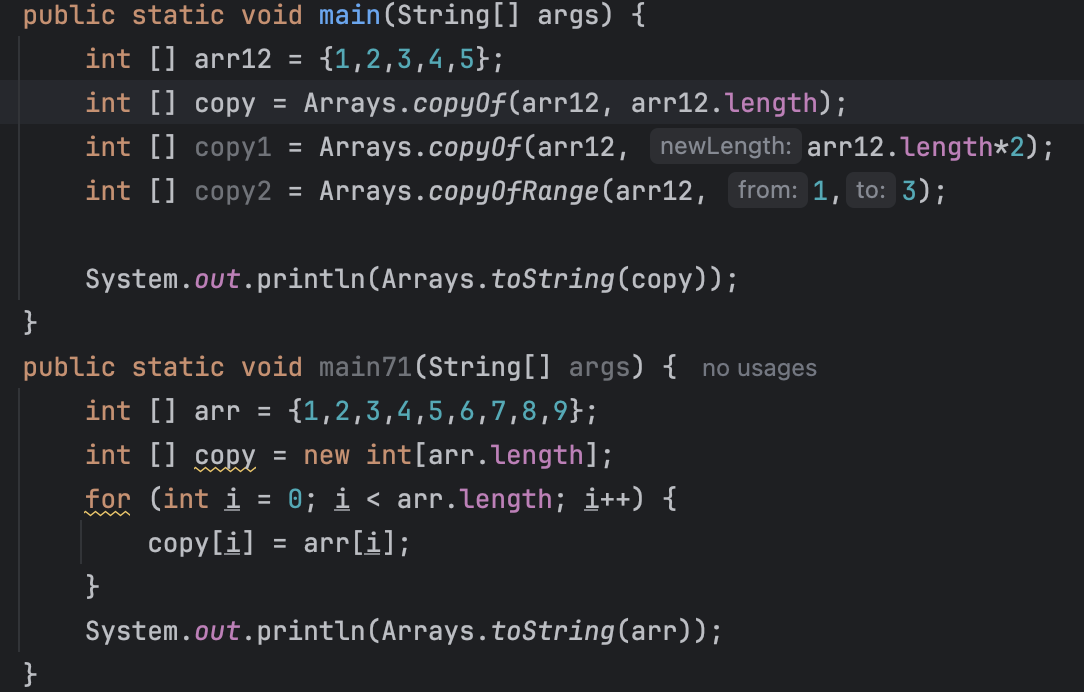
高数
第二型曲线积分计算
类对称(看微元方向)
一投二代三计算
格林公式
- 曲线封闭无奇点
- 曲线封闭有奇点
- 非封闭曲线,二维旋度为0,换路径
- 非封闭曲线,旋度不为0,添线使之封闭(加线减线)
- 积分与路径无关的六个等价命题
两类曲线积分关系(二型与一型)
Pdx+Qdy+Rdz=(P,Q,R)*(cosα,cosβ,cosγ)ds
注意单位切向量的求解;起点参数a小于终点参数b时,取正;反之取负;
空间问题
- 一投二代三计算
- 斯托克斯[注意斯托克斯对于二型一型的形式,其中对于一型,(cosα,cosβ,cosγ)为Σ的单位外法线向量]
- rot F = 0(无旋场),换路径
第二型曲面积分计算
类对称(流入为负流出为正)
一投二代三计算
转换投影法(三面投一面),此时要考虑单位向量方向
高斯公式
- 封闭曲面无奇点,直接用
- 封闭曲面、有奇点在其内部,且除奇点外div F = 0,可换个面积分(边界无须和原曲面重合)
- 非封闭,且div F = 0,可换个面积分,但是边界需与原曲面重合
- 非封闭,且 div F ≠ 0,补面使其封闭(加面减面)
- 由div F = 0,建方程求f(x)
两类曲面积分关系
(P,Q,R)(dydz,dzdx,dxdy)=(P,Q,R)(cosα,cosβ,cosγ)dS,其中(cosα,cosβ,cosγ)为Σ在点(x,y,z)同侧的单位法向量一些其他:换元时要记得算雅各比行列式的绝对值

![[JVM]对象创建过程](https://img2024.cnblogs.com/blog/1533409/202409/1533409-20240916220416831-1736522444.png)
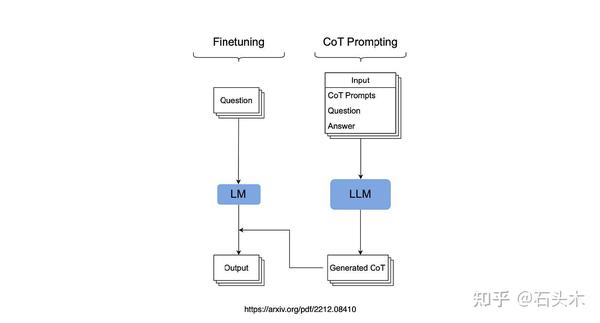
![[WesternCTF2018]shrine](https://img2024.cnblogs.com/blog/3374335/202409/3374335-20240916214544638-468027328.png)



![day1闯关作业小结[linux基础知识]](https://img2024.cnblogs.com/blog/3229976/202409/3229976-20240916201714685-825603912.png)