题目1 669. 修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:

输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]
示例 2:

输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
思路
既然搜索后要继续保持树为二叉搜索树,则应该移除范围外的节点,并保留范围内的节点。因此,当节点的val不在范围内时,需要返回相应的左节点或者右节点。
代码
//递归法
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if(root == nullptr){return root;}if(root->val < low){return trimBST(root->right, low, high);}else if(root->val > high){return trimBST(root->left, low, high);}root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};
代码
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {while(root){if(root->val < low)root = root->right;else if(root->val > high)root = root->left;elsebreak;}TreeNode* curNode = root;while(curNode){if(curNode->left && curNode->left->val < low){curNode->left = curNode->left->right;}elsecurNode = curNode->left;}curNode = root;while(curNode){if(curNode->right && curNode->right->val > high){curNode->right = curNode->right->left;}elsecurNode = curNode->right;}return root;}
};
题目2 108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵
平衡
二叉搜索树。
示例 1:

输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:

输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
思路
使用递归和分而治之的思想,每次处理数组中中间的节点,并让中间节点指向新的子节点;使用递归也是类似的思路,每次处理一个范围的中间节点,范围用额外的2个queue来保存。
代码
class Solution {
public:TreeNode* createTree(vector<int>& nums, int lft, int rht){if(lft > rht)return nullptr;TreeNode* curNode = new TreeNode(nums[(rht + lft) / 2]);curNode->left = createTree(nums, lft, (rht + lft) / 2 - 1);curNode->right = createTree(nums, (lft + rht) / 2 + 1, rht);return curNode;}TreeNode* sortedArrayToBST(vector<int>& nums) {return createTree(nums, 0, nums.size() - 1);}
};
题目3 538. 把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
示例 1:
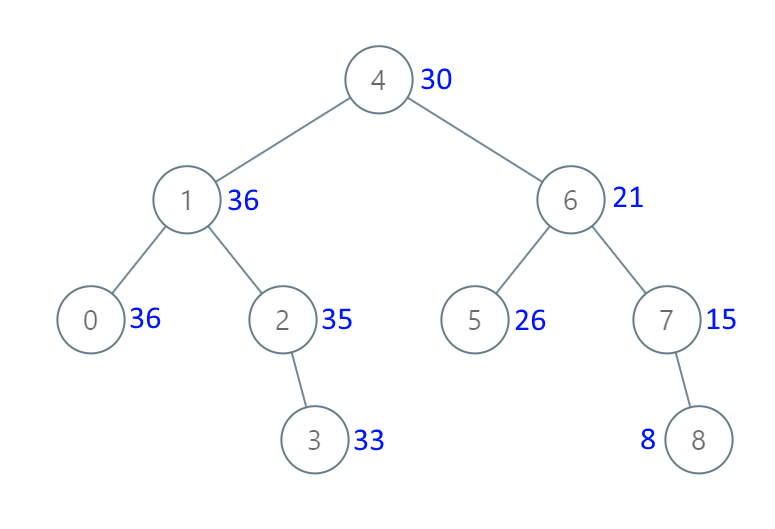
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
思路
因为二叉搜索树的最右侧节点是最大的,因此使用翻转过的中序遍历,按照右当前节点左的顺序遍历并累加节点值就能保证生产的结果为累加树。
递归法
class Solution {
public:int curNum = 0;TreeNode* convertBST(TreeNode* root) {if(root == nullptr)return root;root->right = convertBST(root->right);root->val += curNum;curNum = root->val;root->left = convertBST(root->left);return root;}
};
迭代法
class Solution {
public:TreeNode* convertBST(TreeNode* root) {if(root == nullptr)return root;stack<TreeNode*> nodeStack;nodeStack.push(root);int num = 0;while(!nodeStack.empty()){TreeNode* curNode = nodeStack.top();if(curNode != nullptr){nodeStack.push(nullptr);if(curNode->right){nodeStack.push(curNode->right);}}else{nodeStack.pop();curNode = nodeStack.top();nodeStack.pop();curNode->val += num;num = curNode->val;if(curNode->left){nodeStack.push(curNode->left);}}}return root;}
};