堆的应用-编程知识

堆的应用

news/2024/9/19 14:15:42/文章来源:https://www.cnblogs.com/madadam/p/18411128

1.需要具备的知识

1.1以顺序存储方式存储完全二叉树

完全二叉树:节点从上到下，从左到右布局的二叉树，如下图所示。

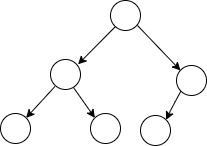
完全二叉树可以使用类似数组这种顺序存储的结构存节点，如下图。

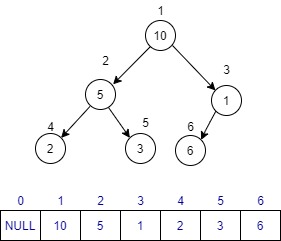
按照"层级遍历"方式遍历这棵树(还有"前序、中序、后序"遍历方式，这里不做介绍)，遍历结果"10->5->1->2->3->6"保存到数组中。为了方便计算父子节点对应关系，不使用数组第一个元素。
如果一个节点在数组中的下标是curIdx,那么如果存在，其对应的左右孩子节点下标lcIdx,rcIdx,以及对应的父节点下标pIdx分别为:

lcIdx=2*curIdx;
rcIdx=2*curIdx;
pIdx=curIdx/2;

1.2堆介绍

堆是一种特殊的完全二叉树，分为大顶堆和小顶堆。大顶堆满足每个节点的值都大于或等于其孩子节点的值；小顶堆满足每个节点的值都小于或等于其孩子节点的值。如下图所示，以下部分我们全部以大顶堆为例。

1.3堆化和建堆

堆化是指将某一个节点放到正确的位置，使得这个节点满足堆的属性。分为两种方式:从下向上堆化和从上向下堆化。

1.3.1从下向上堆化

使用场景是将元素一个一个插入到堆中，先将新元素做为叶子节点放到最后位置，然后将该节点向上堆化，最终落到满足堆特性的位置，如下图所示。
1.新节点值为9，先放入到最后位置。
2.9大于其父节点8，交换两个节点。
3.新的9节点继续和其父节点比较，小于10，堆化结束。

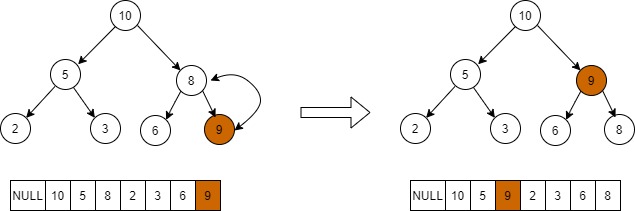
代码实现如下,nums存储的是堆节点数据。

//从下往上堆化一个节点
void HeapifyFromBToUp(vector<int>&nums,int heapIdx)
{while(heapIdx>1) //heapIdx为1的根节点没有父节点,故不用再处理{if(nums[heapIdx]>nums[heapIdx/2])//当前堆化节点的值大于其父节点的值{//交换两个节点的值int temp = nums[heapIdx/2];nums[heapIdx/2]=nums[heapIdx];nums[heapIdx]=temp;heapIdx = heapIdx/2;//继续向上堆化}else{//当前堆化节点在正确位置，堆化结束break;}}
}
void insertIntoHeap(vector<int>&nums,int value)
{nums.push_back(value);//先将新节点插入到最后HeapifyFromBToUp(nums,nums.size()-1);//对新节点向上堆化
}

1.3.2从上向下堆化

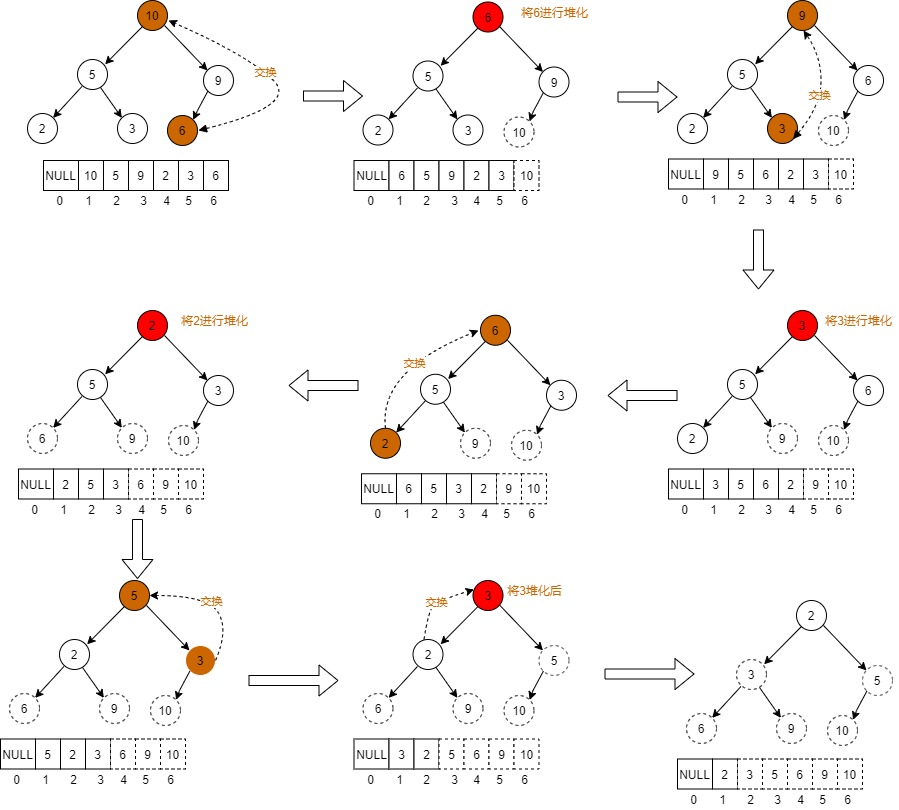
使用场景是将已经存在的完全二叉树，从最后一个非叶子节点开始，将该节点向下堆化，最终落到满足堆特性的位置，如下图所示。最后一个非叶子节点下标为数组长度/2，这里为7/2=3。
1.节点6小于其唯一的左孩子节点9，二者交换，节点6堆化完成。
2.节点3与其左右两个节点比较，三个节点最大是10，交换10节点和3节点，节点3堆化完成。
3.节点5与其左右两个节点比较，三个节点最大是10，交换10节点和5节点，节点5堆化完成。至此，所有节点堆化完成。

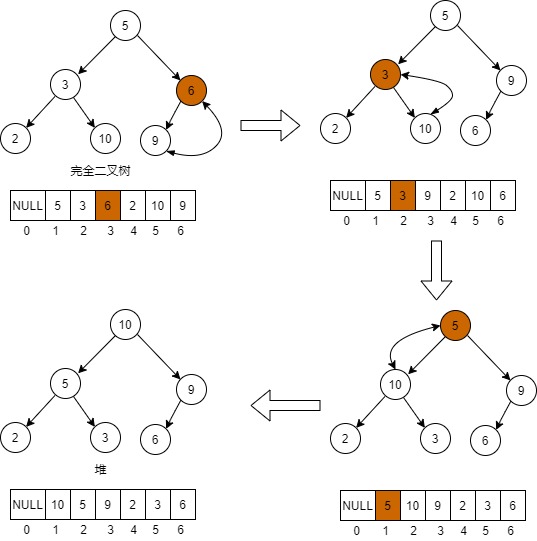
代码实现如下：nums存储的是树节点数据。

//从上向下堆化一个节点heapIdx，这里的n在排序时有用，后面讲解。void HeapifyFromUpToB(vector<int>&nums,int n,int heapIdx){int size = n;int temp=0;while(true){//找到堆化节点heapIdx和其左右孩子节点中的最大值int maxIdx = heapIdx;if(2*heapIdx<size && nums[2*heapIdx]>nums[maxIdx])maxIdx = 2*heapIdx;if(2*heapIdx+1<size && nums[2*heapIdx+1]>nums[maxIdx])maxIdx = 2*heapIdx+1;if(maxIdx==heapIdx)//堆化节点位置正确，堆化结束break;//交换堆化节点和最大值节点temp=nums[heapIdx];nums[heapIdx]=nums[maxIdx];nums[maxIdx]=temp;//heapIdx=maxIdx; //如果只是构建堆可以不用这行，但是在排序时有用，后面讲解(巧妙) }}//建堆void heapBuilder(vector<int>&nums){int size = nums.size();//for(int i=size/2;i>=1;--i)HeapifyFromUpToB(nums,size,i);//逐个堆化非叶子节点}

2.应用-查找topK

在大量数据文件中找到第K小的那个数据，可能是GB或TB级别的数据量。如果先实现排序再返回第K小的数据，占用内存空间复杂度太高O(n)，如果用快排等思想，时间复杂度为O(nlogn)，这种方法不合适。
我们可以维护一个大小为K的大顶堆，这个大顶堆的目的是存储前K小的数据。遍历数据文件，
1.如果新数据比栈顶小则说明当前栈顶肯定不满足前K小，将当前栈顶元素更新为新数据，并对新栈顶节点进行堆化处理。因为是对栈顶节点堆化，只能用从上向下的堆化方式。
2.如果新数据不比栈顶元素小，则不做处理。
相信有了上面建堆和堆化的方法，不难实现该功能，这里不再列出源代码了。