存储论——确定性存储模型模型精解

运筹学中的存储问题主要研究如何通过优化库存管理，确保在满足需求的同时，尽可能降低与库存相关的成本。这一问题在生产制造、物流运输、仓储等各个领域具有重要应用。核心目标是通过合理规划进货、存货和出货策略，实现成本最小化和资源的高效利用。在实际应用中，由于需求的不确定性、供应链的复杂性，以及库存管理成本的多样性，存储问题往往变得更加复杂。因此，如何在动态多变的环境下制定最佳存储策略，成为运筹学中的重要研究课题之一。通过对存储系统的分析，可以帮助企业在应对不确定性需求时，确保库存充足、避免缺货，同时减少库存积压、降低持有成本。此外，运筹学还通过构建不同的库存模型（如经济订货批量模型、随机库存模型等），为企业提供在不确定环境下管理库存的科学依据，从而提升运营效率并增强企业的竞争力。

存储系统	经济订货批量

一、存储系统概述

存储的最终目的就是协调供求关系，为了考察最佳的库存方案，这里首先分析存储系统包含哪些要素(环节)。物资的存储包括生产存储，为了维持企业正常生产而储备的原材料或半成品；产品存储，为了满足其他部门的需要而存储的半成品或成品；供销存储，为了满足顾客的需要，存储在供销部门的各种物资。不论哪种存储系统，都可用图下图来表示。

存储系统	间断式	连续式

存储系统可以用“供—存—销”三个字来描述，即一个存储系统，通过订货以及进货后的存储与销售来满足顾客的需求。

存储系统的输出
从存储系统中取出一定数量的库存货物，这就是存储系统的输出。存储系统的输出方式有间断式和连续式两种，如上图所示，其中 S 是初始库存量，经过时间T 后，库存量是W，输出了S-W。 需求方每次提出的需求量可能是确定的，也可能是随机的。如某工厂每月需要钢材 10 吨是固定不变的，而对机器零件的需求量却是每月都在变，如 1 月需要 40 个、2 月需要 55 个、3 月需要 30 个等，一般根据大量的统计数据，找出需求量满足的统计规律。

存储系统的输入
本章默认凡待使用的或待销售的物资即是进入了库存。库存物资由于不断地输出而减少，必须进行及时补充，库存的补充就是存储系统的输入，它可以通过订货、采购等活动来进行，也可以通过内部的生产活动来进行。正如我们熟知的，一个商店为了提高顾客选购商品的满意度，就必须储存商品。这样商店首先要掌握进货渠道，即供货市场，关注供货市场的变化规律和行情。其次商店还应掌握需求市场，即顾客对商品的需求规律、需求方式等。清楚了供应和需求的变化规律，商店才可根据自己的情况，应用库存论的方法来控制实际库存。存储系统的运行规律主要
是由供应市场与需求市场的运行规律所决定的，而实际中供应与需求的规律是多种多样的。这些不同的规律，显然从根本上决定了库存系统的运行规律。在存储系统中对库存进行管理是必要的，它在整个供应—生产—分配过程中起着缓冲的作用。由于需求量往往是系统外部决定的，因而存储系统的输出难以控制和掌握，但可以控制影响存储系统输入的因素，这些因素主要是补充库存的时间以及补充的数量等参数。为了保持库存，需要进行订货，由于开始订货到进货有一段时间，因此为保证及时供应，就要提前订货，提前的时间称为“提前订货时间”，提前订货时间可以是确定的，也可以是随机的。

二、 存储系统的费用及变量

存储系统的决策者可以通过控制订货时间的间隔和订货量的多少来调节系统的运行，使得在某种准则下系统运行达到最优。因此要明确该存储系统所发生的费用和有关的决策变量。

2.1 存储系统的费用

费用是存储管理的一个重要经济指标，存储系统必须按最经济的原则运行，为了建立存储模型必须了解各类存储系统费用的构成情况。
(1) 订货费。对供销型存储系统来说，订货费是指为补充库存，办理一次订货发生的有关费用，包括订货过程中发生的订购手续费、联络通信费、人工核对费、差旅费、货物检查费、入库验收费等。
当生产型存储系统自行组织生产时，订货费相当于组织一次生产所必需的工具安装、设备调整、试车、材料安排等费用。订货费一般与订购或生产的数量无关或基本无关。在确定订货费时，对具体问题要具体分析，但必须注意不能将搬运费、管理费等平均分摊到每件货物上去，这样就会导致订货费和一次订购的数量有关了。在年消耗量固定不变的情况下，一次订货量越大，订货次数就越少，订货费就越少。因此，从订货费角度看，订货批量越大越好。
(2) 存储费。存数就越少，订货费就越少。因此，从订货费角度看，订货批量越大越好。
(2) 存储费。存储费一般是指库存物资每单位时间所需花费的费用，也称持有成本。在这一项费用中，只计入与库存物资数量成正比的部分，凡与存储物资数量无关的不变费用不计算在内。有时存储费还经常用每存储 1 元物资单位时间所支付的费用来表示，称为存储费率。
存储费包括存储物资所占用资金的利息，物资的存储损耗、陈旧和跌价损失，存储物资的保险费，仓库建筑物及设备的修理折旧费、保险费，存储物资的保养费，库内搬运设备的动力费，搬运工人的工资等。在以上存储费用中，利息支出所占比重较大。以工业贷款月利率 0.6%计算，存储百万元物资一年，仅利息就需支付 7.2 万元。由此可见，控制存储物资数量，对加速物资周转的意义很大。
由于订货量越大，平均库存量就越大，因而存储费支出越大。因此，从存储费角度看，订货批量越大越不好。
(3) 缺货费。在存储系统中，还有一种费用是存储系统管理者不愿发生的费用，这就是缺货费。这项费用是因为供需脱节造成生产停顿而进行计划调整的损失费，或突击加班所增加的额外开支，未能完成合同任务而使需方损失给供方带来的赔款损失费等，还可能是因为无货满足顾客而降低服务质量、损失信誉及潜在盈利机会，流失顾客而造成销售不良的损失等。总之，这是由于缺货而未能满足需求所带来的各种损失的费用表现。在有些情况下是不允许缺货的。例如，战争中缺少军械、弹药等将造成人员重大伤亡乃至战败，血库缺血将威胁生命等，这时的缺货费可视为无穷大。
(4) 生产费(买价)。如果库存不足需要补充，可选外购或自行生产。外购时，需支付买价(当有折扣时更要考虑买价)；自行生产时，这里的生产费用专指与生产产品的数量有关的费用，如直接材料、直接人工、变动的制造费用。

2.2 存储系统的变量

在存储系统中经常分析以下变量。
(1) 订货批量(Q)。存储系统根据需求，为补充某种物资的存储量而向供货厂商一次订货或采购的数量。
(2) 订货周期(T )。两次订货的时间间隔或订货合同中规定的两次进货之间的时间间隔。
(3) 报警点( s )。报警点又称订货点，该点库存量和提前订货时间是相对应的，当库存量下降到这一点时，必须立即订货，当所订的货物尚未到达及入库之前，存储量应能按既定的服务水平满足提前订货时间的需求。
(4) 安全库存量( ss )。安全库存量又称保险储备量。由于需求量( D )和提前订货时间(t )都可能是随机变量，随其波动幅度的增大可能大大超过其平均值。为了预防和减少这种随机性造成的缺货，必须准备一部分库存，这部分库存称为安全库存量。只有出现缺货情况时才动用安全库存量。
(5) 最高库存量( S )。在提前订货时间可以忽略不计的存储模型中，最高库存量是指每次到货后所达到的库存量。当存在提前订货时，最高库存量是指发出订货要求后，库存量应该达到的数量，由于此时并未实际到货，因此该最高库存量又称名义库存量。
(6) 最低库存量。一般是指实际的库存最低数量。
(7) 平均库存量(\(\bar{Q}\))。库存保有的平均库存量，当存在报警点(s)时，平均库存量为\(\bar{Q} = \frac{1}{2} Q + s\)
(8) 记账间隔期( R)。记账间隔期是指库存记账制度中的间断记账所规定的时间，即每隔记账间隔期的时间，整理平时积欠下来的发料原始凭据，并进行记账，得到账面结存数以检查库存量。

2.3 存储策略和存储模型分类

在存储系统中，将物质保持在预期的一定水平，使得生产和流通过程不间断并有效的进行，需对输入过程中的订货时间和订货数量进行控制，称为存储策略。存储策略确定后，首先是把实际问题抽象为数学模型，对一些复杂的条件尽量加以简化，只要模型能反映问题的本质就可以了；然后用数学的方法对模型进行求解，得出数量的结论；结论是否正确，还要到实践中加以检验，如结论不符合实际，则还要对模型加以修改，重新建立、求解、检验，直到满意为止。
存储系统的常用存储策略
存储系统包含定量订购和定期订购两大类。

• 定量订购制
  泛指通过公式计算或经验求得报警点$ s $ 和每次订货量$ O \(，并且每当库存量下降到\) s $ 点时，就进行订货的存储策略。通常使用的有 (Q, s)、(S, s)、(R, S, s) 制等。
• (Q, s) 制
  • 采用这种策略需要确定订货批量$ Q $ 和报警点$ s $ 两个参数。
  • (Q, s) 属于连续监控制（又称永续盘点制），即每供应一次就结算一次账，得出一个新的账面数字并和报警点$ S $ 进行比较。
  • 当库存量达到$ s $ 时，就立即以$ O $ 进行订货。
• (S, s) 制
  • 这种策略是 (Q, s) 制的改进，需要确定最高库存量$ S $ 及报警点$ s $ 两个参数。
  • (S, s) 制属于连续监控制。
  • 每当库存量达到或低于$ s $ 时，就立即订货，使订货后的名义库存量达到$ S \(。因此，每次订货的数量\) O $ 是不固定的。
• 定期订购制
  即每经过一段固定的时间间隔$ T $（称订货周期）就补允订货使存储量达到某种水平的存储策略。常用的有 (T, S) 制。
  • (T, S) 制
  • 需要确定订购间隔期$ T $ 和最高库存$ S $ 两个参数。
  • 即每隔时间$ T $ 检查库存，根据剩余存储量和估计的需求量确定订货量$ O \(，使库存量恢复到最高库存\) S $。

存储模型分类
为便于讨论，根据不同的供求规律、库存产品的种数和考虑的时间周期对存储系统进行分类。

确定型与随机型存储模型

• 凡需求量$ D \(、提前订货时间\) t $ 为确定已知的存储问题所构成的存储模型为确定型。
• 凡上述二者之一或全部为随机变量的存储问题构成的存储模型为随机型。
  在确定型存储模型中，又可分为需求不随时间变化和需求随时间变化两种类型；同样，随机型存储模型也可根据需求量是否随时间变化分为两类。
  （2）单周期与多周期存储模型
  有的物资必须购进后一次全部供应或售出，否则就会造成经济损失，这类存储问题的模型成为单周期存储模型，如报纸、年历等时令性物品以及防洪、防冻季节性物资构成的模型。有的物资多次进货多次供应，形成进货——供应消耗——再进货——再供应消耗，周而复始的形成多周期特点的存储问题的模型称为多周期存储模型。
  （3）单品种与多品种存储模型
  一般地，将数量大、体积大又占用金额多的物资单独设库管理，称为单品种库。如木材、水泥、焦炭、煤等，这类库存往往占用大量资金，要采用比较精细的方法来计算其存储控制参数。有些物资是多品种存放在一个仓库里的称为多品种库。如钢材库、电器元件库、配件库、有色金属库等。多品种库的存储不可能逐一计算每种物资的库存控制参数，可以将库存物资按其占用金额进行 分类进行存储管理。由于流动资金定额一般是按仓库下达的，所以多个品种物资存放在一个仓库时，往往存在资金约束及仓库容积约束，这样的存储模型称为带约束的存储问题。本章着重介绍单品种存储模型，多品种存储问题可同样讨论。
  在存储模型中，目标函数是选择最优策略的准则。常见的目标函数是关于总费用或平均费用或折扣费用（或利润）的，最优策略的选择应使费用最小或利润最大。综上所述，一个存储系统的完整描述需要知道需求、供货滞后时间、缺货处理方式、费用结构、目标函数以及所采用的存储策略、决策者通过何时订货、订多少货来对系统实施控制。

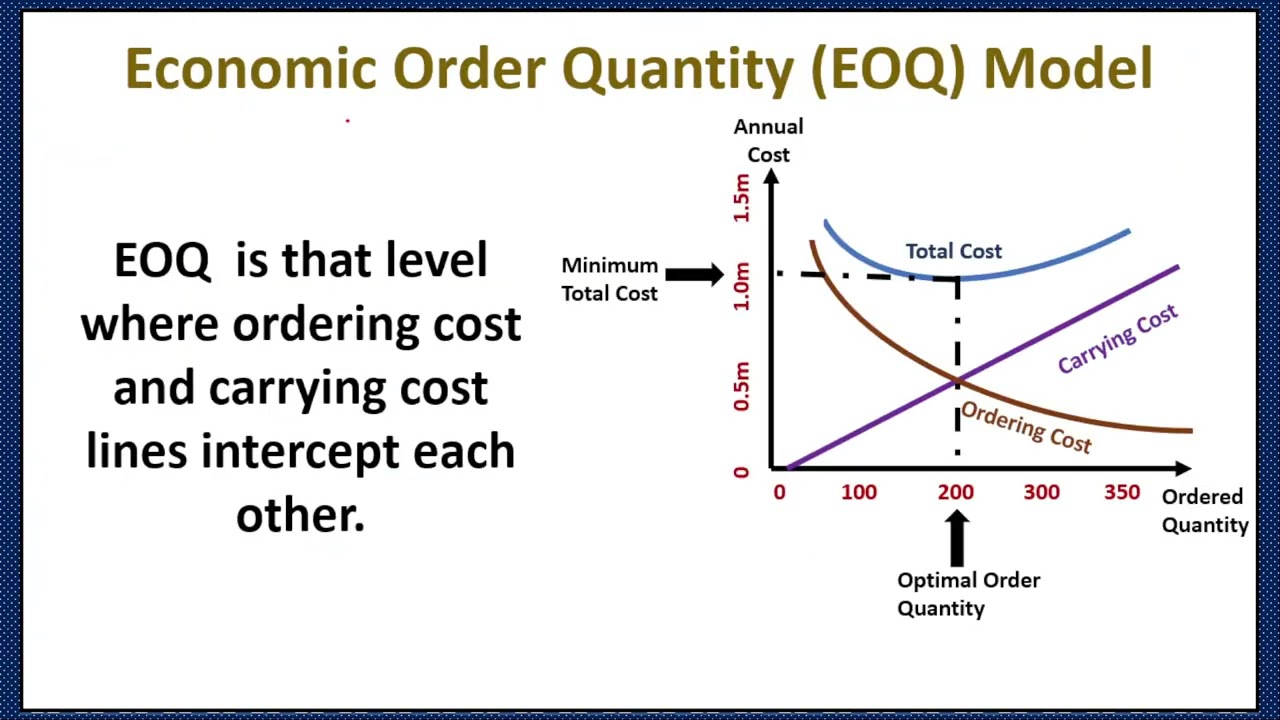
三、经典的经济订货批量EOQ模型

• 模型假设
  ①缺货费用无穷大；
  ②当库存降至零时，可以立即得到补充（即生产时间很短，可以近似地看作零）；
  ③需求是连续的、均匀的；
  ④每次订货量不变，订购费不变（每次生产量不变，装配费不变）；
  ⑤单位存储费不变。
  这就是著名的经济订货批量EOQ（Economic Order Quantity）模型假设。经济订货批量模型又称整批间隔进货模型EOQ模型，该模型适用于整批间隔进货、不允许缺货的存储问题，即某种物资单位时间的需求量为常数 ，存储量以单位时间消耗数量 的速度逐渐下降，经过时间 后，存储量下降到零。此时开始定货并随即到货，库存量由零上升为最高库存量 ，然后开始下一个存储周期，形成多周期存储模型。
  该模型的需求量和提前订货时间是确定的，只要确定每次订货的数量是多少或进货间隔期为多长时间，就可以做出存储策略。由于存储策略是使存储总费用最小的经济原则来确定订货批量，故称该订货批量为经济订货批量。

存储量变化	存储费用曲线

• 模型的有关参数
  \(T\) ——订货周期或存储周期（年或月或日）；
  \(D\) ——需求数量, 即单位时间的需求量 (件 / 年或件 / 月或件 / 日);
  \(Q\) ——每次订货批量（件或全）；
  \(c_1\) ——存储单位物资单位时间的存储费（元 / 件・年或元 / 件・月或元 / 件・日）；
  \(c_3\) ——每次订货的订货费（元）；
  \(K\) ——货物单价（元 / 件）。
• 模型建立和求解
  模型的存储量变化见上图。一个订货周期内需要该种物资 \(Q=D T\) 个，图中存储量斜线上的每一点表示在该时刻的库存水平, 每一个订货周期存储量的变化形成一个直角三角形。一个订货周期的平均存储量为 \(\frac{1}{T} \int_0^T D t d t=\frac{1}{2} Q\) ，存储费用为 \(\frac{1}{2} c_1 Q T\) ；一次订货费为 \(c_3\), 一个存储周期的订货总费用 \(c_3+D K T\), 因此, 在这个存储周期内总费用为 \(\frac{1}{2} c_1 Q T+c_3+D KT\)

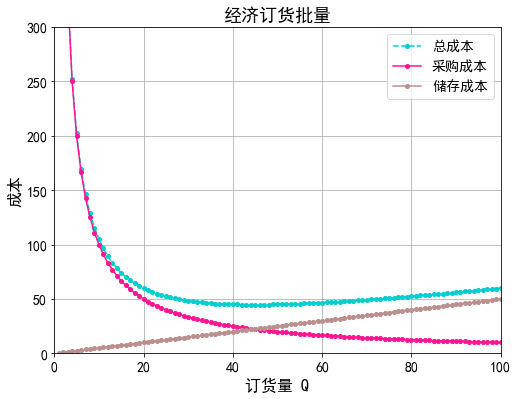
由于订货周期 \(T\) 是变量, 为便于比较, 计算单位时间的平均总费用, 即$$C_z=\frac{1}{2} c_1 Q+\frac{c_3}{T}+DK$$
将 \(T=Q / D\) 代入, 得$$C_Z=\frac{1}{2} c_1 Q+\frac{c_3 D}{Q}+DK$$
显然, 单位时间的订货费随着订货批量的增大而减小, 而单位时间的存储费随着订货批量 \(Q\) 的增大而增大, 见上图。
求导数$$\frac{d C_Z}{d Q}=\frac{1}{2} c_1-\frac{c_3 D}{Q^2}=0$$
即得经济订货批量$$Q^=\sqrt{\frac{2 c_3 D}{c_1}}tag{1}$$
这是因为 \(\frac{d^2 C_Z}{d Q^2}=\frac{2 c_3 D}{Q^2}>0\) ，故当 \(Q^*=\sqrt{\frac{2 c_3 D}{c_1}}\) 时， \(C_Z\) 取最小值。
公式（1）称为经济订货批量公式，由于威尔逊是该公式推导应用的倡导者，所以该公式也称为威尔逊公式。
由式 (1) 及 \(Q^*=T D\) 可得到订货周期 \(T^*=\sqrt{\frac{2 c_3}{D c_1}}\) ，将 \(Q^*=\sqrt{\frac{2 c_3 D}{c_1}}\) 代入（9-1）式前一部分, 立刻得到按经济订货批量进货时的最小存储总费用为$$C^=\sqrt{2 D c_1 c_3}$$
由于 \(Q^*, T^*\) 均与 \(K\) 无关，所以此后的费用函数中省略去 \(D K\) 项。还要说明的是，前面在确定经济订货批量中, 认为订货和进货可以同时发生, 实际上, 定货和到货一般总有一段时间间隔, 为保证供应的连续性, 需要提前订货。设提前订货时间为 \(t\), 日需要量为 \(D\), 则订购点 \(s=D t\), 当库存下降到 \(s\) 时, 即按经济订货批量 \(Q^*\) 订货, 在提前订货时间内, 以每天 D 的速度消耗库存, 当库存下降到零时, 恰好收到订货, 开始一个新的存储周期。
对于以上确定型存储问题, 最常使用的策略就是经济订货批量 \(Q^*\), 并每隔时间 \(T^*\) 即订货, 使存储量恢复到最高库存量 \(Q\), 这是实际中最常用的经济订货批量公式。该存储策略可以认为是定量订购制, 但因订购周期也固定, 又可以认为是定期订购制。

例：某企业每年对某种零件的需求量为 20000 件, 每次订货的固定订货费用为 1000 元, 该零件的单价为 30 元, 每个零件每年的保管费用为 10 元, 求经济订货批量, 每年的库存总成本, 每年的订货次数和每次订货的时间间隔。(一年按 360 天计)
解: 据题知 \(D=20000\) 件、 \(c_1=10\) 元/件、 \(c_3=1000\) 元/次、 \(K=30\) 元/件, 则
(1) 订货批量 \(Q^*=\sqrt{\frac{2 c_3 D}{c_1}}=\sqrt{\frac{2 \times 1000 \times 20000}{10}}=2000\) (件);
(2）每年的最小存储总费用 \(C^*=\sqrt{2 c_1 c_3 D}=\sqrt{2 \times 1000 \times 10 \times 20000}=20000\) (元),考虑购买成本的总费用为$$T C=D K+C^=20000 \times 30+20000=620000(\text { 元 })$$
(3）每年的购买次数 \(N=D / Q=20000 / 2000=10\) （次）;
(4）每次订货的时间间隔 \(T^*=\sqrt{\frac{2 c_3}{c_1 D}}=\sqrt{\frac{2 \times 1000}{10 \times 2000}}=\frac{1}{10}\) 年 \(=\frac{1}{10} \times 360=36\) （天）。
若以 \(D\) 表示某种物资的年需用量, \(K\) 表示该物资的单价, \(c_3\) 为一次订货费, \(r\) 表示存储费率, 即存储每元物资一年所需的存储费用, 则得到经济订货批量的另外一种常用形式$$Q^=\sqrt{\frac{2 c_3 D}{r K}}$$

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm# 配置中文字体，确保能正确显示中文，并调大字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题# 全局调整字体大小
plt.rcParams.update({'font.size': 14})  # 将字体整体调大一号# 参数定义
C1 = 1  # 假设的值，替换为实际的C1
C3 = 1000  # 假设的值，替换为实际的C3
R = 1   # 假设的值，替换为实际的R# 定义x范围，从1开始避免除零错误，x轴固定范围为0-100
x = np.linspace(1, 100, 100)# 定义y1, y2, y3
y1 = C3 * R / x
y2 = C1 * x / 2
y3 = y1 + y2# 创建图形
plt.figure(figsize=(8, 6))# 绘制总成本
plt.plot(x, y3, marker='o', color='DarkTurquoise', label="总成本", linestyle='--', markersize=4)# 绘制采购成本
plt.plot(x, y1, marker='o', color='DeepPink', label="采购成本", linestyle='-', markersize=4)# 绘制储存成本
plt.plot(x, y2, marker='o', color='RosyBrown', label="储存成本", linestyle='-', markersize=4)# 设置坐标范围，x轴固定在0-100
plt.xlim(0, 100)
plt.ylim(0, 300)# 设置坐标轴标签和标题，字体大小设为16
plt.xlabel('订货量 Q', fontsize=16)
plt.ylabel('成本', fontsize=16)
plt.title('经济订货批量', fontsize=18)# 添加图例，字体大小设为14
plt.legend(loc='upper right', fontsize=14)# 显示网格
plt.grid(True)# 显示图形
plt.show()

总结

运筹学中的存储问题研究旨在优化库存管理，以在复杂的供需环境中实现成本的最小化和效率的最大化。虽然经济订货批量模型等基本策略在需求稳定的情况下效果显著，但现实中的需求往往是随机且不确定的，因此存储问题逐渐发展出更加复杂的模型，如随机库存模型和多层级供应链模型等。这些模型考虑了需求的不确定性、供应链延迟、价格波动等实际因素，为企业提供了更加精细和灵活的库存管理方案。通过优化进货、存货和出货策略，企业可以有效应对需求的波动，减少持有成本和缺货风险，从而提升运营效率。在现代复杂的供应链环境中，运筹学为企业提供了科学的工具，使其能够应对快速变化的市场需求。运用这些模型和策略，不仅能够帮助企业在供需不平衡时保持高效运作，还能够在长远发展中获得持续的竞争优势。

参考资料

1. 存储论（二）：有约束的确定型存贮模型、单周期随机库存模型
2. 数学建模之存储论