?

CF1194G

在外层枚举\(x'\)和\(y'\),令\(x=x'\times t,y=y'\times t\)，且\(x'\times t\)十进制包含\(x'\)，\(y'\)同理。

因为有进位，从低位向高位dp。

设\(f[T][0/1][0/1][i][j][0/1][0/1]\)表示处理到第T位，在当前这些为中\(x'\times t\)是否大于\(n\),\(y'\times t\)是否大于\(n\),\(x'\times t\)进位为\(i\),\(y'\times t\)进位为\(j\)，其中\(i,j<=8\)，\(x'\times t\)是否存在\(x'\)这个数码，\(y'\times t\)是否存在\(y'\)这个数码。

转移是简单的，但是会算重。

例如\(\frac{14}{28}\)就会被\(\frac{1}{2}\)和\(\frac{4}{8}\)同时贡献到。

也就是\(\frac{x0'}{y0'}=\frac{x1'}{y1'}\)时会算重。

在外层枚举最简分数\(\frac{x''}{y''}\)，然后枚举\(\frac{x''}{y''}=\frac{x'}{y'}\),只要\(x''\times t\)包含任意一个\(x'\)这个数码，同时\(y''\times t\)包含这个\(y'\)数码，那么我们直接加两维，设\(k\)为满足\(\frac{x''}{y''}=\frac{x'}{y'}\)的\((x',y')\)数量，新加的两维每维大小为\(2^k\),判掉\(x''=1,y''=1\)以后\(k\)最大为\(4\)

状态数为\(n\times 2^2 \times 9^2 \times 2^{2k}\)，但是过不了。

我们发现若\(\frac{x}{y}\)合法，则\(\frac{y}{x}\)合法，可以枚举外层时令\(x''<y''\)，常数小一半，然后我们发现若\(x''\times t\)超过了\(n\)，那么\(y''\times t\)一定也超过了\(n\)，所以前者毫无意义，所以又可以少一半常数。

然后我们又发现，\(k\)在很大一部分的情况下是很小的，\((x'',y'')\)只有\(27\)对，但是\((x',y')\)只有\(45\)对，这里可以优化常数。

然后我们又又又发现，我们只关心存不存在\(x''\times t\)包含任意一个\(x'\)这个数码，同时\(y''\times t\)包含这个\(y'\)数码，对于每一个\((x',y')\)，记录\(0/1/2\)表示,都两个条件都不满足，只满足\(x'\)的条件和只满足\(y'\)的条件，如果当前两个条件都满足了就没必要记录这个东西了。

这样\(2^{2k}\)就变成了\(3^k\)，常数更进一步。

UOJ888. 【UNR #8】里外一致

设c[i]为第i种颜色的出现次数

考虑设f[i][j]为考虑前i种颜色，里外颜色之差为j，不难转移，时间复杂度\(O(n^2)\)

考虑改一下定义，设f[i][j]为考虑前i种颜色，有j个只在里侧或只在外侧，有：
\(f[t][i]\rightarrow f[t+1][i]\)，系数为\(2^{c_{t+1}}-2\)

\(f[t][i]\rightarrow f[t+1][i+1]\)，系数为\(1\)

最后答案为\(\sum_{k=0}C(k,k/2)f_{n,k} [k \bmod 2=0]\)

注意到第一种转移最多64次，因为系数有因数2，超过64次在对\(2^{64}\)取模意义下为0。

考虑换一下定义，j改为有j个里外侧都有，那么转移如下：

\(f[t][i]\rightarrow f[t+1][i+1]\)，系数为\(2^{c_{t+1}}-2\)

\(f[t][i]\rightarrow f[t+1][i]\)，系数为\(1\)

计算答案：

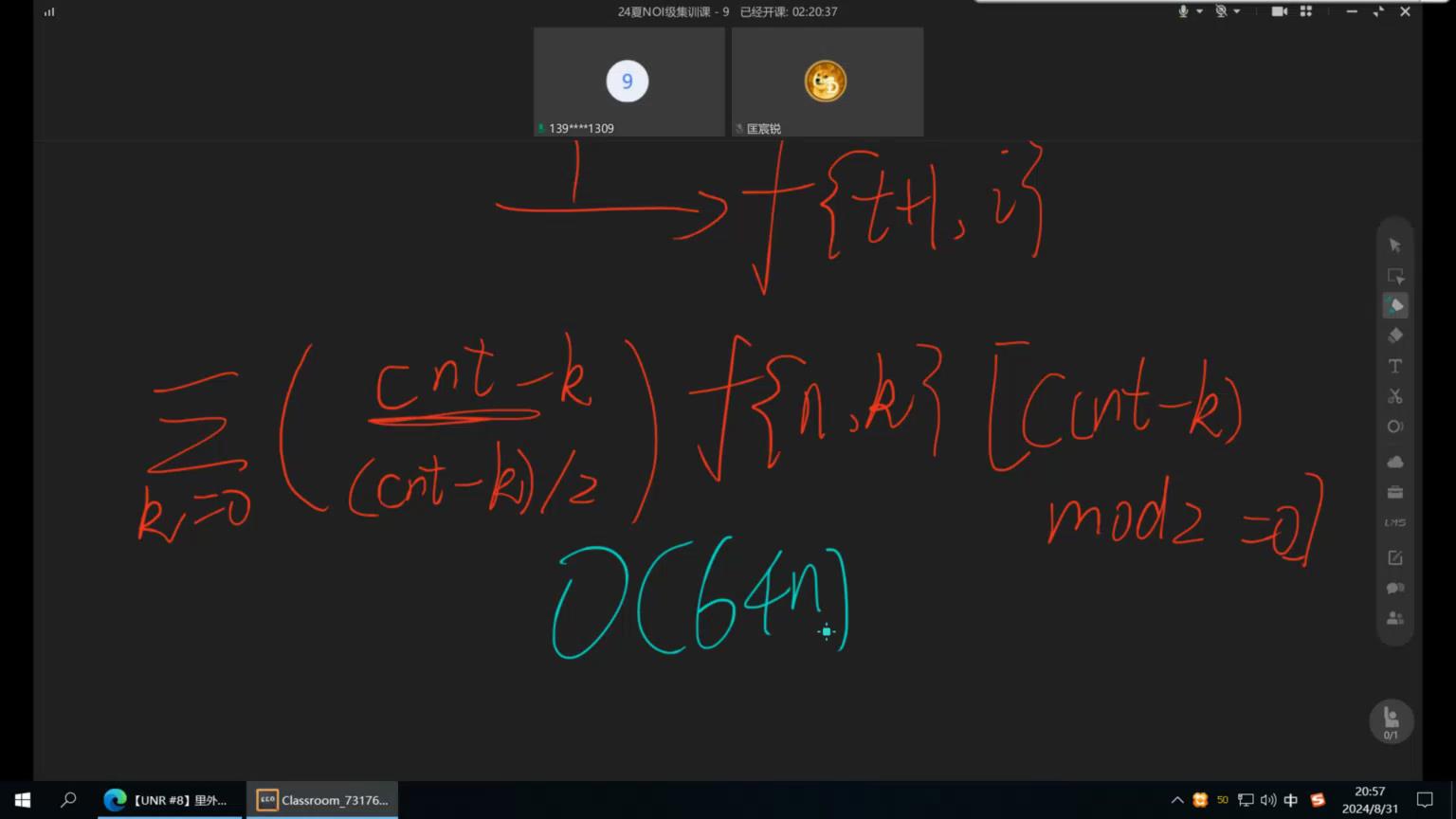
现在\(i\)的范围在为\(i<=64\)，单次时间复杂度为\(O(64n)\)

考虑把出现次数一样的颜色一起处理。

我们令\(z[i]\)表示\([l,r]\)内出现了\(i\)次的颜色有\(g[i]\)种。

考虑处理所有出现次数为d的颜色。

设\(f[d-1][i]\)表示考虑了出现次数不超过\(d-1\)的颜色，有i种在两侧都有，转移方程为：

\(f[d-1][i]\rightarrow f[d][i+k]\)，系数为\(C(z_d,k)(2^d-2)^k\)

考虑到\(i\)和\(k\)的大小都不超过\(64\)，单次时间复杂度为\(O(n+n\times 64^2)\)，但真的是这样吗？

我们发现最多有\(\sqrt n\)个\(d\)使得\(z_d!=0\)，所以单次时间复杂度其实是\(O(n+\sqrt n \times 64^2)\)

我们考虑上一个莫队，再来一个数据结构（set或zkw线段树）找到每一个不为\(0\)的\(c_i\)，可以以总时间复杂度\(O(n log n\sqrt n)\)内计算出\(c_i\)和\(z_d\)

总时间复杂度为\(O(n log n\sqrt n + m(\sqrt n \times 64^2))\)，考虑优化右侧\(dp\)的那一部分。

我们观察模数为\(2^{64}\)能不能再次帮助我们优化时间复杂度，把转移系数拿出来：\(C(z_d,k)(2^d-2)^k\)，观察\((2^d-2)\)，发现若\(d>64\)就变成了\(-2\)，而且前面莫队那里不用数据结构了，总时间复杂度为\(O(n\sqrt n+m64^3)\)

考虑使用一点几何意义，2的因子越多我们的算法越优。

观察\((2^d-2)^k\)，假定没有这个\(-2\)，就变成了\((2^d)^k\)，这时要满足\(i+c\times k<=64\),也就是时间复杂度是这样的形式：

$\sum_{c=1}^{64} \sum_{i=1}^n \left \lfloor \frac{64-i}{c} \right \rfloor $

但是还有一个\(-2\)没有还回来，于是我们枚举一个i,令g为原来的f,f为不考虑-2算出的结果。

有\(f[cnt][i]\rightarrow g[cnt][i+j]\)系数为\(C(cnt-i,j)\)

计算出g，这题就做完啦。

总时间复杂度为\(O(n\sqrt n+m64^2)\)