[ABC221H] Count Multiset

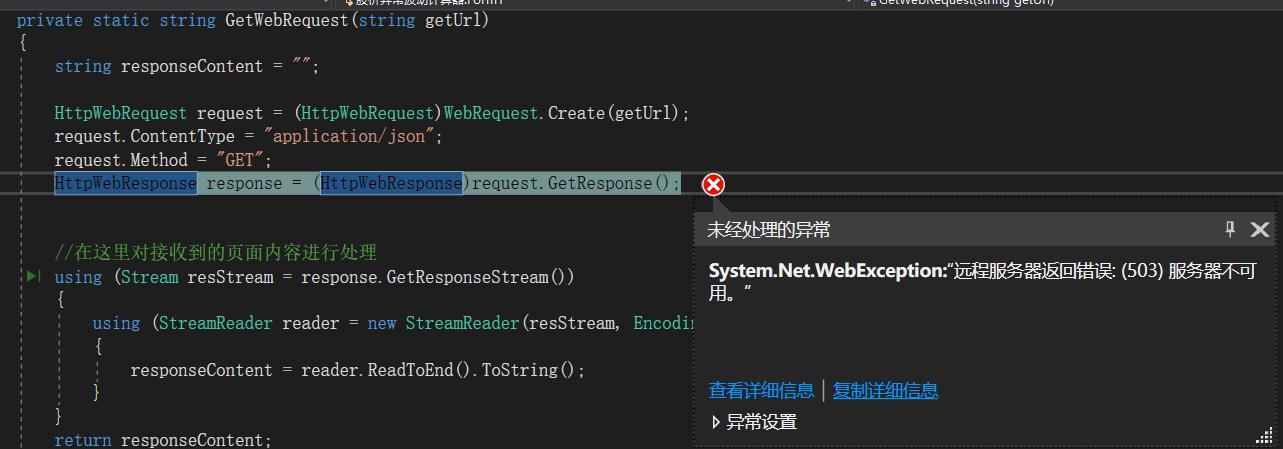
题意

思路

参考了题解做法。

设 \(f_{i, j}\) 表示填入 \(i\) 个数字，和为 \(j\) 的方案数。

每次可以填入 \(0\)，或者将整个数列 \(+1\)。

\(g_{i, j}\) 表示填入 \(i\) 个数字，且这 \(i\) 个数字中没有 \(0\)，何为 \(j\) 的方案数。

易得 \(g_{i, j} = f_{i, j - i}\)，表示在 \(i\) 个数字的和为 \(j - i\) 的情况下给每个数字 \(+1\)，这样保证了所有数字均不为 \(0\)。

下面看 \(f\) 的转移。

\(f_{i, j} = \sum\limits_{k = 1} ^ {m} g_{i - k, j}\) 表示填入 \(k\) 个 \(0\)。

\(f_{i, j} = f_{i, j - i}\)，表示全体 \(+1\)。

代码

#include <bits/stdc++.h>using namespace std;const int N = 5010, mod = 998244353;int f[N][N];
int g[N][N];
int sum[N][N];
int n, m;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cin >> n >> m;for (int i = 1; i <= m; i++) f[i][0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (j >= i) {g[i][j] = f[i][j - i];f[i][j] = f[i][j - i];}sum[i][j] = (sum[i - 1][j] + g[i][j]) % mod;int l = i - m, r = i - 1;(f[i][j] += (sum[r][j] - sum[max(0, l - 1)][j]) % mod) %= mod;}}for (int i = 1; i <= n; i++) cout << (g[i][n] + mod) % mod << '\n';return 0;
}