P2414 [NOI2011] 阿狸的打字机

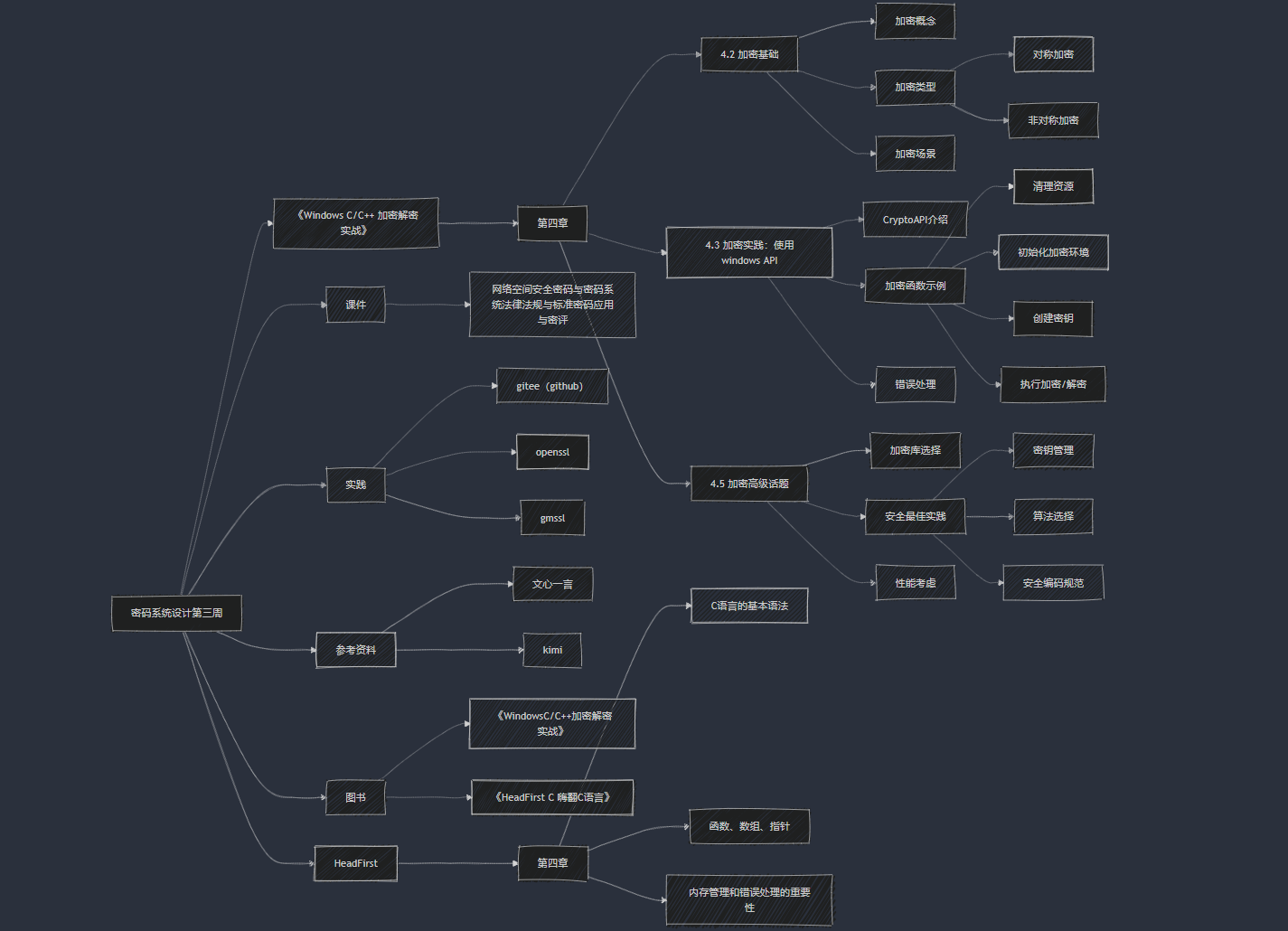
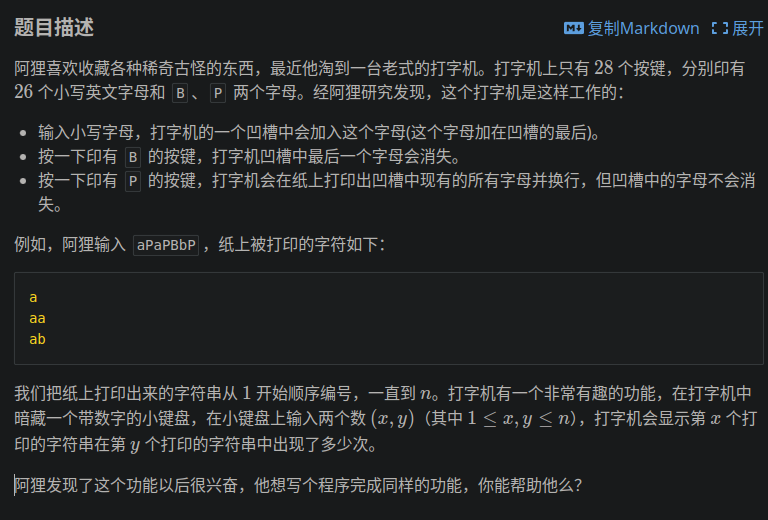
题目

思路

将每一个输出的串放入一个 Trie 树中。

考虑离线处理询问 \((x, y)\)，对于每一个 \(y\) 集中处理所有的 \(x\)，\(y\) 在 Trie 树上走，走过的点标记一下，结果就是 \(x\) 字符串结尾节点在 fail 树上的对应节点的子树的标记数量。

记得在节点离开的时候撤销标记。

代码

#include <bits/stdc++.h>using namespace std;const int N = 100010, M = 2600010;struct edge {int to, next;
} e[M];int head[M], idx = 1;void add(int u, int v) {idx++;e[idx].to = v;e[idx].next = head[u];head[u] = idx;
}string opt_str;
int q, ans[N];
vector<pair<int, int> > query[N];struct ac {int son[26];int fa;int fail;
} t[N];int ac_idx;
int val[N];void insert() {int p = 0, str_idx = 0;for (auto x : opt_str) {if (x >= 'a' && x <= 'z') {int u = x - 'a';if (!t[p].son[u]) t[p].son[u] = ++ac_idx;t[t[p].son[u]].fa = p;p = t[p].son[u];}else if (x == 'B') p = t[p].fa;else {str_idx++;val[str_idx] = p;}}
}void getfail() {queue<int> q;for (int i = 0; i < 26; i++) {if (t[0].son[i]) {q.push(t[0].son[i]);}}while (q.size()) {int g = q.front();q.pop();for (int i = 0; i < 26; i++) {if (t[g].son[i]) {t[t[g].son[i]].fail = t[t[g].fail].son[i];q.push(t[g].son[i]);}else t[g].son[i] = t[t[g].fail].son[i];}}for (int i = 1; i <= ac_idx; i++) add(t[i].fail, i);
}int dfn[N], sz[N], dfn_idx;void dfs(int u, int fa) {sz[u] = 1, dfn[u] = ++dfn_idx;for (int i = head[u]; i; i = e[i].next) {int to = e[i].to;if (to == fa) continue;dfs(to, u);sz[u] += sz[to];}
}int tr[N];void modify(int u, int x) {if (u <= 0) return;for (; u < N; u += u & -u) {tr[u] += x;}
}int ask(int u) {if (u <= 0) return 0;int ans = 0;for (; u; u -= u & -u) ans += tr[u];return ans;
}void getans() {int p = 0, str_idx = 0;for (auto x : opt_str) {if (x >= 'a' && x <= 'z') {int u = x - 'a';p = t[p].son[u];modify(dfn[p], 1);}else if (x == 'B') {modify(dfn[p], -1);p = t[p].fa;}else {str_idx++;for (auto [x, y] : query[str_idx]) {int ver = val[x];ans[y] = ask(dfn[ver] + sz[ver] - 1) - ask(dfn[ver] - 1);}}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cin >> opt_str >> q;for (int i = 1; i <= q; i++) {int l, r;cin >> l >> r;query[r].push_back({l, i});}insert();getfail();dfs(0, 0);getans();for (int i = 1; i <= q; i++) cout << ans[i] << '\n';return 0;
}