排队论——随机服务系统仿真精解

排队论作为研究随机服务系统的重要工具，专门研究系统中客户到达、排队、服务和离开的过程。排队论的核心目的是通过数学建模和分析，研究系统的性能指标，如平均等待时间、队列长度、系统的吞吐量等。虽然排队论提供了强大的数学工具来分析随机服务系统，但在许多复杂的实际问题中，精确的数学模型可能难以建立。这时候，模拟与仿真技术便成为了研究和优化系统的重要方法。
模拟是通过计算机程序对一个真实系统进行近似模拟的过程。通过在仿真中引入随机变量，可以对系统的随机行为进行研究，从而评估系统在不同条件下的性能表现。仿真不仅可以用于验证理论模型，还能用于探索无法通过解析方法解决的复杂系统。与排队论的解析模型不同，模拟与仿真更灵活，可以处理非标准的、复杂的排队系统。一个典型的应用场景是机场的安检系统。乘客到达安检口的时间、安检速度、安检通道数量等因素都具有随机性。通过仿真技术，可以对不同配置方案下的乘客等待时间、系统吞吐量等性能指标进行估计，从而为决策者提供优化方案。

单服务台	多服务台

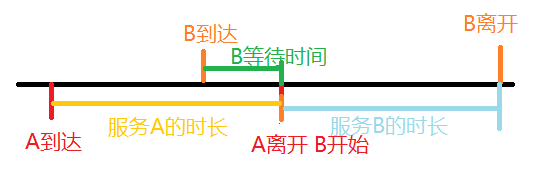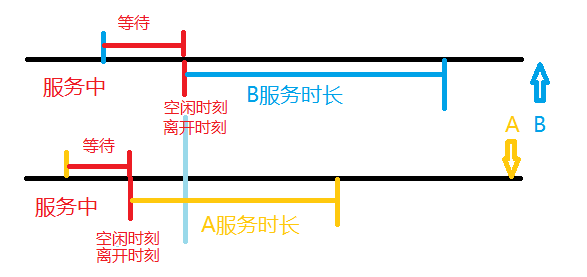一、Python仿真库概述

仿真库名	用途	概述	功能特点
SimPy	离散事件仿真	简单易用的离散事件仿真库，适合模拟排队系统、生产线、交通系统等。	支持并发进程，简单易用，适用于大多数离散事件仿真需求。
DEAP	蒙特卡洛仿真、遗传算法仿真	用于演化计算的库，适合用于遗传算法、遗传规划、模拟进化过程、解决优化问题等。	支持遗传算法、演化策略等，支持分布式计算，适合优化问题、复杂的决策系统。
PyDSTool	动力学系统仿真	适用于连续和混合动力系统仿真的工具库。	支持符号数学和自动微分，适合科学研究和复杂系统的仿真。
SALib	敏感性分析、蒙特卡洛仿真	用于敏感性分析的库，常与蒙特卡洛仿真结合使用。	支持全局和局部敏感性分析，可以用于评估输入参数对模型输出的影响，常与其他仿真库结合使用。
PySim	系统建模与仿真	通用的仿真框架，适合模拟各种物理系统。	支持多学科系统仿真，支持FMI标准，适用于复杂的工程仿真需求。
AnyLogic	系统动力学、离散事件、Agent-Based仿真	商业化的仿真平台，提供Python接口来进行定制化仿真。	提供Python接口来扩展仿真能力，适合大规模工业仿真，可用于供应链管理、物流、生产制造等领域。
Gym	强化学习仿真	用于强化学习的仿真环境库。	预设了多种仿真环境，适合强化学习和动态系统仿真，灵活的接口，可以自定义仿真环境。
Mesa	基于Agent的仿真	基于Agent的仿真框架，适合用于模拟复杂系统中的个体行为和交互。	易于使用的API，快速构建多智能体模型，提供图形化界面和可视化工具，适合社会学、经济学、生态学等领域。

二、M/M/1排队系统模型仿真

2.1 M/M/1排队系统的绩效指标

在M/M/1排队模型中，系统只有一个服务机构，顾客到达的时间间隔和服务时间都服从指数分布。通过M/M/1模型，可以计算系统的各项性能指标。下面我们先给出6个常见的性能指标的计算公式，然后提供一个Python程序来计算这些指标。

常用符号

• λ: 到达率（每单位时间内的平均顾客到达数量）
• μ: 服务率（每单位时间内的平均服务数量）
• ρ: 系统的利用率（利用率 = λ/μ）

绩效指标及公式

• 系统利用率 \(ρ (ρ = λ/μ)\):系统中服务器被占用的比例。
• 系统中平均客户数 \(L (L = ρ / (1 - ρ))\):系统中的平均客户数，包括排队和正在接受服务的客户。
• 队列中的平均客户数 \(L_q (L_q = ρ^2 / (1 - ρ))\):系统中正在排队的平均客户数，不包括正在服务的客户。
• 系统中客户的平均逗留时间 \(W (W = 1 / (μ - λ))\):系统中每个客户的平均停留时间，包括等待和服务时间。
• 客户在队列中的平均等待时间 \(W_q (W_q = ρ / (μ - λ))\):每个客户在排队中等待的平均时间，不包括服务时间。
• 空闲概率 $P_0 (P_0 = 1 - ρ):系统处于空闲状态（即无客户到达或正在服务）的概率。

# 定义计算性能指标的函数
def mm1_performance(lmbda, mu):# 系统利用率 rhorho = lmbda / muif rho >= 1:raise ValueError("系统利用率不能大于或等于1，说明到达率必须小于服务率。")# 系统中平均客户数 LL = rho / (1 - rho)# 队列中的平均客户数 LqLq = rho**2 / (1 - rho)# 系统中客户的平均逗留时间 WW = 1 / (mu - lmbda)# 客户在队列中的平均等待时间 WqWq = rho / (mu - lmbda)# 空闲概率 P0P0 = 1 - rho# 返回结果return {"系统利用率 (rho)": rho,"系统中平均客户数 (L)": L,"队列中的平均客户数 (Lq)": Lq,"系统中客户的平均逗留时间 (W)": W,"客户在队列中的平均等待时间 (Wq)": Wq,"空闲概率 (P0)": P0}# 固定的到达率和服务率
lmbda = 3  # 到达率 λ
mu = 5     # 服务率 μ# 计算并输出各个性能指标，保留两位小数
try:performance = mm1_performance(lmbda, mu)for key, value in performance.items():print(f"{key}: {value:.2f}")
except ValueError as e:print(e)

系统利用率 (rho): 0.60
系统中平均客户数 (L): 1.50
队列中的平均客户数 (Lq): 0.90
系统中客户的平均逗留时间 (W): 0.50
客户在队列中的平均等待时间 (Wq): 0.30
空闲概率 (P0): 0.40

2.2 M/M/1排队系统仿真分析

import simpy
import random
import matplotlib.pyplot as plt
from matplotlib import rcParams# 设置中文字体
rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
rcParams['axes.unicode_minus'] = False    # 正常显示负号# 设置种子以确保仿真结果的可重复性
RANDOM_SEED = 42
random.seed(RANDOM_SEED)# 定义全局变量
lmbda = 3  # 到达率 λ (每单位时间的顾客到达数)
mu = 5     # 服务率 μ (每单位时间的服务能力)
SIM_TIME = 1000  # 仿真运行时间class MM1Queue:def __init__(self, env, mu):self.env = envself.server = simpy.Resource(env, capacity=1)  # 1表示单个服务器self.mu = muself.total_waiting_time = 0.0self.total_system_time = 0.0self.total_customers = 0self.system_size = 0  # 系统中顾客人数self.time_data = []  # 时间点self.size_data = []  # 系统中顾客人数def serve(self, customer):"""顾客服务时间"""yield self.env.timeout(random.expovariate(self.mu))def arrival(self, customer):"""顾客到达"""arrival_time = self.env.nowself.system_size += 1  # 系统中顾客人数 +1self.record_data()  # 记录当前时刻的顾客人数with self.server.request() as request:yield request  # 等待服务waiting_time = self.env.now - arrival_time  # 计算等待时间self.total_waiting_time += waiting_timeself.total_customers += 1yield self.env.process(self.serve(customer))  # 开始服务self.system_size -= 1  # 系统中顾客人数 -1self.record_data()  # 记录当前时刻的顾客人数# 计算系统内停留时间system_time = self.env.now - arrival_timeself.total_system_time += system_timedef record_data(self):"""记录当前仿真时间和系统中顾客人数"""self.time_data.append(self.env.now)self.size_data.append(self.system_size)def run(self):"""顾客不断到达"""customer_id = 0while True:yield self.env.timeout(random.expovariate(lmbda))  # 顾客到达时间间隔customer_id += 1self.env.process(self.arrival(customer_id))def simulate_mm1():# 初始化环境env = simpy.Environment()mm1_queue = MM1Queue(env, mu)# 运行仿真env.process(mm1_queue.run())env.run(until=SIM_TIME)# 计算系统性能指标L = mm1_queue.total_system_time / SIM_TIME  # 系统中平均客户数Lq = mm1_queue.total_waiting_time / SIM_TIME  # 队列中的平均客户数W = mm1_queue.total_system_time / mm1_queue.total_customers  # 系统中客户的平均逗留时间Wq = mm1_queue.total_waiting_time / mm1_queue.total_customers  # 客户在队列中的平均等待时间# 输出结果print(f"系统中平均客户数 (L): {L:.2f}")print(f"队列中的平均客户数 (Lq): {Lq:.2f}")print(f"系统中客户的平均逗留时间 (W): {W:.2f}")print(f"客户在队列中的平均等待时间 (Wq): {Wq:.2f}")# 绘制时间-顾客人数曲线图plt.plot(mm1_queue.time_data, mm1_queue.size_data)plt.xlabel('仿真时间')plt.ylabel('系统中顾客人数')plt.title('M/M/1 排队系统仿真')plt.grid(True)plt.show()# 运行仿真并输出结果
simulate_mm1()

系统中平均客户数 (L): 1.59
队列中的平均客户数 (Lq): 1.00
系统中客户的平均逗留时间 (W): 0.54
客户在队列中的平均等待时间 (Wq): 0.34

三、M/M/c排队系统仿真分析

3.1 M/M/c排队系统的绩效指标

对于 M/M/c 系统，常见的6个性能指标及其计算公式如下：
常用符号

• λ: 到达率（每单位时间内的平均顾客到达数量）
• μ: 服务率（每单位时间内的平均服务数量）
• c: 为服务台的数量

绩效指标及公式

• 系统利用率 $ \rho（\rho = \frac{\lambda}{c\mu} $）：表示系统的平均工作负荷，或是所有服务台的平均占用率。
• 队列中的平均顾客数 \(L_q(L_q = \frac{P_0 (\lambda/\mu)^c \rho}{c! (1 - \rho)^2})\)：表示在队列中等待服务的平均顾客数量。这里，\(P_0\) 是系统空闲时的概率。
• 系统中平均顾客数 $L（L = L_q + \frac{\lambda}{\mu} $）：表示在整个系统（包括正在接受服务的顾客）中的平均顾客数量。
• 顾客在队列中的平均等待时间 $ W_q (W_q = \frac{L_q}{\lambda} $）：表示顾客在队列中等待服务的平均时间。
• 顾客在系统中的平均逗留时间 $ W ( W = W_q + \frac{1}{\mu} $）：表示顾客在整个系统中（包括服务时间）的平均逗留时间。
• 系统空闲的概率 $ P_0( P_0 = \left[ \sum_{n=0}^{c-1} \frac{(\lambda/\mu)^n}{n!} + \frac{(\lambda/\mu)^c}{c!(1 - \rho)} \right]^{-1} $）：表示系统中没有顾客时的概率，即所有服务台均空闲的概率。

import math# 输入数据
lmbda = 0.9  # 到达率 λ (人/分钟)
mu = 0.4     # 服务率 μ (人/分钟)
c = 3        # 售票窗口数# 系统利用率 ρ
rho = lmbda / (c * mu)# 计算 P0 (系统空闲的概率)
def calculate_P0(lmbda, mu, c):sum_terms = sum((lmbda / mu) ** n / math.factorial(n) for n in range(c))last_term = ((lmbda / mu) ** c) / (math.factorial(c) * (1 - rho))P0 = 1 / (sum_terms + last_term)return P0# 计算 Lq (队列中的平均顾客数)
def calculate_Lq(lmbda, mu, c, rho, P0):numerator = P0 * (lmbda / mu) ** c * rhodenominator = math.factorial(c) * (1 - rho) ** 2Lq = numerator / denominatorreturn Lq# 计算各项指标
P0 = calculate_P0(lmbda, mu, c)  # 系统空闲的概率
Lq = calculate_Lq(lmbda, mu, c, rho, P0)  # 队列中的平均顾客数
L = Lq + lmbda / mu  # 系统中平均顾客数
Wq = Lq / lmbda  # 顾客在队列中的平均等待时间
W = Wq + 1 / mu  # 顾客在系统中的平均逗留时间# 输出结果
print(f"系统利用率 (ρ): {rho:.2f}")
print(f"系统空闲的概率 (P0): {P0:.4f}")
print(f"队列中的平均顾客数 (Lq): {Lq:.2f}")
print(f"系统中平均顾客数 (L): {L:.2f}")
print(f"顾客在队列中的平均等待时间 (Wq): {Wq:.2f} 分钟")
print(f"顾客在系统中的平均逗留时间 (W): {W:.2f} 分钟")

3.2 M/M/c排队系统仿真分析

import simpy
import random
import matplotlib.pyplot as plt
from matplotlib import rcParams# 设置中文字体支持
rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体显示中文
rcParams['axes.unicode_minus'] = False    # 解决负号显示问题# 输入数据
RANDOM_SEED = 42
lmbda = 0.9  # 到达率 λ (人/分钟)
mu = 0.4     # 服务率 μ (人/分钟)
c = 3        # 售票窗口数
SIM_TIME = 1000  # 仿真时间（分钟）random.seed(RANDOM_SEED)class MMcQueue:def __init__(self, env, num_servers, mu):self.env = envself.server = simpy.Resource(env, capacity=num_servers)self.mu = muself.total_waiting_time = 0.0self.total_system_time = 0.0self.total_customers = 0self.customers_in_queue = 0self.queue_time = 0.0self.system_customers = []# 记录仿真过程中各时刻的系统内顾客人数self.time_data = []self.num_customers_data = []def serve(self, customer):"""服务过程，顾客服务时间"""service_time = random.expovariate(self.mu)yield self.env.timeout(service_time)def arrival(self, customer):"""顾客到达"""arrival_time = self.env.nowself.system_customers.append(len(self.server.queue) + len(self.server.users))# 记录当前时刻的顾客人数self.record_customers_count()# 顾客加入队列with self.server.request() as request:yield requestwaiting_time = self.env.now - arrival_time  # 计算顾客等待时间self.total_waiting_time += waiting_timeself.queue_time += len(self.server.queue)self.total_customers += 1# 开始服务yield self.env.process(self.serve(customer))# 系统内停留时间 = 当前时间 - 到达时间system_time = self.env.now - arrival_timeself.total_system_time += system_time# 记录当前时刻的顾客人数self.record_customers_count()def record_customers_count(self):"""记录当前仿真时刻的系统内顾客人数"""current_time = self.env.nownum_customers = len(self.server.queue) + len(self.server.users)self.time_data.append(current_time)self.num_customers_data.append(num_customers)def run_simulation(env, num_servers, mu):mmc_queue = MMcQueue(env, num_servers, mu)def customer_arrivals():customer_id = 0while True:# 顾客到达时间inter_arrival_time = random.expovariate(lmbda)yield env.timeout(inter_arrival_time)customer_id += 1env.process(mmc_queue.arrival(customer_id))# 启动顾客到达过程env.process(customer_arrivals())# 运行仿真env.run(until=SIM_TIME)# 计算系统性能指标Lq = mmc_queue.total_waiting_time / SIM_TIME  # 队列中的平均顾客数L = sum(mmc_queue.system_customers) / len(mmc_queue.system_customers)  # 系统中平均顾客数Wq = mmc_queue.total_waiting_time / mmc_queue.total_customers  # 顾客在队列中的平均等待时间W = mmc_queue.total_system_time / mmc_queue.total_customers  # 顾客在系统中的平均逗留时间# 输出结果print(f"队列中的平均顾客数 (Lq): {Lq:.2f}")print(f"系统中平均顾客数 (L): {L:.2f}")print(f"顾客在队列中的平均等待时间 (Wq): {Wq:.2f} 分钟")print(f"顾客在系统中的平均逗留时间 (W): {W:.2f} 分钟")# 绘制时间-顾客人数曲线图plt.figure(figsize=(10, 6))plt.plot(mmc_queue.time_data, mmc_queue.num_customers_data, label='系统内顾客人数', color='b')plt.xlabel('仿真时间（分钟）')plt.ylabel('系统内顾客人数')plt.title('M/M/3 排队系统中各时刻的顾客人数')plt.grid(True)plt.legend()plt.show()# 运行仿真
env = simpy.Environment()
run_simulation(env, c, mu)

总结

随着大数据、人工智能、物联网等技术的发展，随机服务系统、排队论与仿真技术的应用前景将更加广阔。一方面，通过融合大数据分析和机器学习算法，可以更准确地预测系统中各类随机事件的发生规律，从而提高系统的效率；另一方面，云计算和高性能计算技术的发展，也使得复杂系统的仿真成为可能。模拟与仿真是解决随机服务系统实际问题的重要工具，通过理论分析和计算机仿真相结合的方式，研究人员和工程师可以优化系统的资源配置、提高服务效率，从而应对复杂系统中的随机性和不确定性。在未来，随着技术的进步，这些方法将会在更多领域得到广泛应用，并为各行各业带来更大的效益。

参考文献

1. 排队模型和排队系统仿真
2. 用R语言模拟随机服务排队系统
3. 排队系统仿真python 排队系统建模仿真