单调栈-滑动窗口

830. 单调栈

模板题：

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式

第一行包含整数 N，表示数列长度。

第二行包含 N 个整数，表示整数数列。

输出格式

共一行，包含 NN 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围

1≤N≤1051≤N≤105
1≤数列中元素≤1091≤数列中元素≤109

输入样例：

5
3 4 2 7 5

输出样例：

-1 3 -1 2 2

AC代码：

#include<iostream>
using namespace std;
const int N=100015;
int e[N],n,tt;
int main(){cin >> n;int m;for(int i=0;i<n;i++){cin >> m;while(tt && e[tt]>=m) tt--;if(tt && e[tt]<=m) cout << e[tt] << " ";else cout << "-1" << " ";e[++tt]=m;}return 0;
}

题解思路：

要求：输出每个数左边第一个比它小的数，如果不存在则输出 −1。

直接上样例：3 4 2 7 5；

首先就考虑边界：第一个数 3 的左边没有数，直接输出 “-1”；

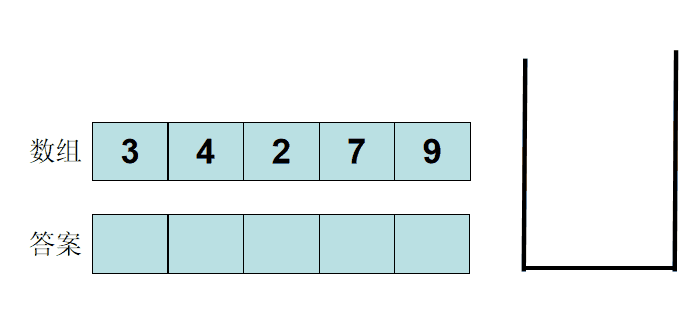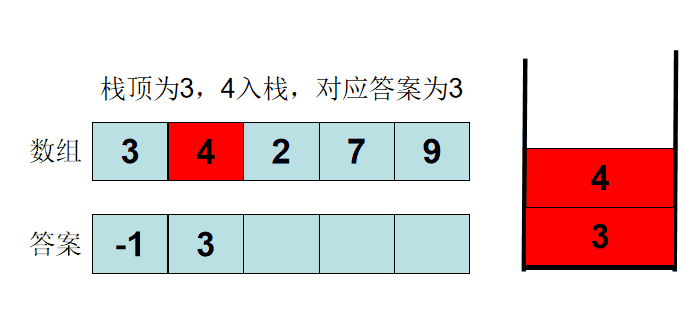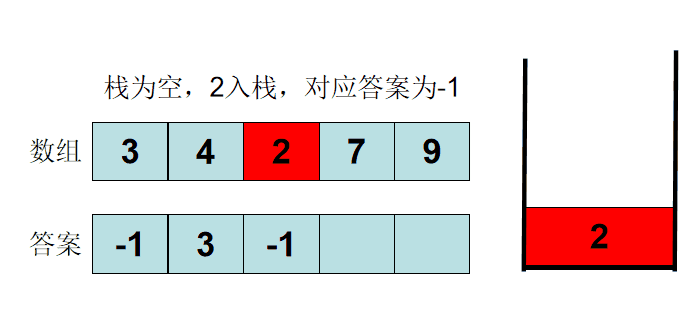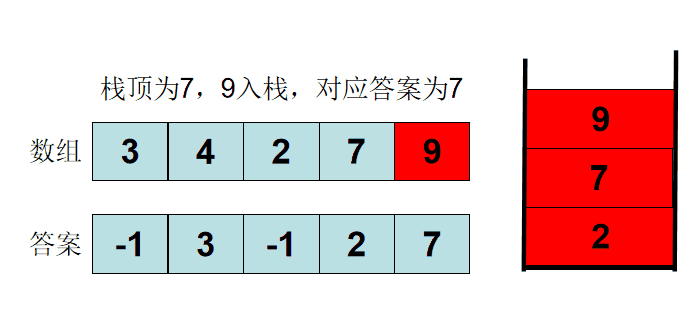
让数值3压入栈中，就可以实现下一个新的数值和栈顶数值进行比较，如果栈顶元素小于新进的元素，那就输出栈顶元素；

现在3压在栈中，数值4对3进行比较，3<4 ,4进入栈中，此时4是栈顶元素，4下一个3不就是离它最近的一个数值嘛？直接输出就好了；

继续下一步：此时的栈底到栈顶顺序是：3 4 ；在用栈顶元素比较新进的元素 2，发现 4 > 2,不符合要求，4出栈，3>2 ，不符合要求，3出栈，不存在要求得数值，输出-1；(那之前栈底元素到栈顶的元素3，4被移除了，怎么能判断左边第一个比它小的数，要知道能找到比3，4更小的靠右的数值2压入栈中，不就可以让3，4正常移除)；

此时还没移动得栈中：3 4 2，用7来找靠左最近得数值，是不是直接找到2，2之前的数就没有判断意义了；

话说得太抽象了,上图解：

---

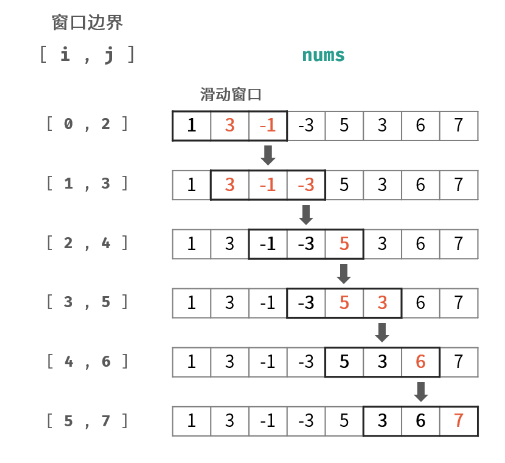
154. 滑动窗口

模板题：

给定一个大小为 n≤10^6 的数组。

有一个大小为 kk 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 kk 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，kk 为 33。

窗口位置	最小值	最大值
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。

第一行包含两个整数 nn 和 kk，分别代表数组长度和滑动窗口的长度。

第二行有 nn 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

AC代码：

#include<iostream>
using namespace std;
const int N=1000015;
//单调队列一般用双端队列保证其单调性
int e[N],b[N],tt=0,dd=-1; 
//在tt对头获得，dd队尾插入；
int main(){int n,m;cin >> n >> m;for(int i=0;i<n;i++)scanf("%d",&e[i]);//先判断区间最小值；for(int i=0;i<n;i++){//tt<=dd 判断队列是否为空，//b[tt]可以理解为固定指向区间最小得指针，每次区间是不一样得，他也就会随着区间得变化变，i-m+1可以理解区间得头指针，只要是头指针没有超过b[tt]那b[tt]就始终是区间得最小值；(i-k+1>=0,就是窗口最小下标要大于等于0);//看分情况讨论：《1》if(tt<=dd && b[tt]<i-m+1)tt++;//《2》//保证单调性，在队尾删除（为什么要在队尾删除，简单来说在队头删除不能保证单调//比如-3 5为当前队列，当前的元素为3，如果在队头操作，那么按照a[i] <= a[q[front]，有3 > -3，因此不做删除操作//但是接下来就出现问题了，3就要入队了。此时队列就是-3 5 3，不符合单调性了！//但如果在队尾操作，按照a[i] <= a[q[tail]，有3 < 5，就要让5出队//之后3入队，队列就是-3 3，满足单调性while(tt<=dd && e[b[dd]]>=e[i]) dd--;b[++dd]=i;//记录最小值得下标//《1.2》里解释if(i>=m-1) cout << e[b[tt]] << " ";}printf("\n");//区间最大值；//和上述同理；for(int i=0;i<n;i++)scanf("%d",&e[i]);int tt=0,dd=-1;for(int i=0;i<n;i++){if(tt<=dd && b[tt]<i-m+1)tt++;while(tt<=dd && e[b[dd]]<=e[i]) dd--;b[++dd]=i;if(i>=m-1) cout << e[b[tt]] << " ";}
}

图解：

问题解析：

• 《1》自定义样例：-1 2 3 1 2 3；

  第一次区间：-1 2 3 1 2 3; i=0;

  第二次区间：-1 2 3 1 2 3;i=1;

  第三次区间：-1 2 3 1 2 3;i=2;

  • 因为 i = 2 满足 if(i>=m-1) cout << e[b[tt]] ；直接输出 ”-1“；
  • 这里解释一下为什么是 m-1；区间是 m = 3,由于队尾插入
    元素初始值是 ”-1“，而 m 是 0；它们之间索引是 m - 1;

  第四次区间：-1 2 3 1 2 3;i=3;

  • 这里我们就可以清晰得看到：b[tt]<i-m+1;b[tt]也就是 ”-1“
    得下标 0 ；而 i-m+1 是 3-3+1；0 < 1, tt++，0+1；就让区间
    -1 2 3 1 2 3 移动一格 -1 2 3 1 2 3；

• 《2》接着上面得样例：-1 2 3 ；

  结合摘抄得注释理解尾删：e[b[dd]]>=e[i] = 2>3 就 dd--；不满足要求；

  数值 3 尾插进入队列：b[++dd]=i (计入数值三下标)，下一步操作；

  -1 2 3 1 2 3；while(tt<=dd && e[b[dd]]>=e[i]) 3> 1 满足要求，dd--;

  2 > 1 满足要求，d--; 到这就别继续减了，tt现在指向的下标为 1；dd=0;不满足条件；

  -1 2 3 1 2 3 对照条件，1是这区间最间最小值；b[++dd]=i，计入，正常输出；