天天爱跑步
假设现在又一棵树
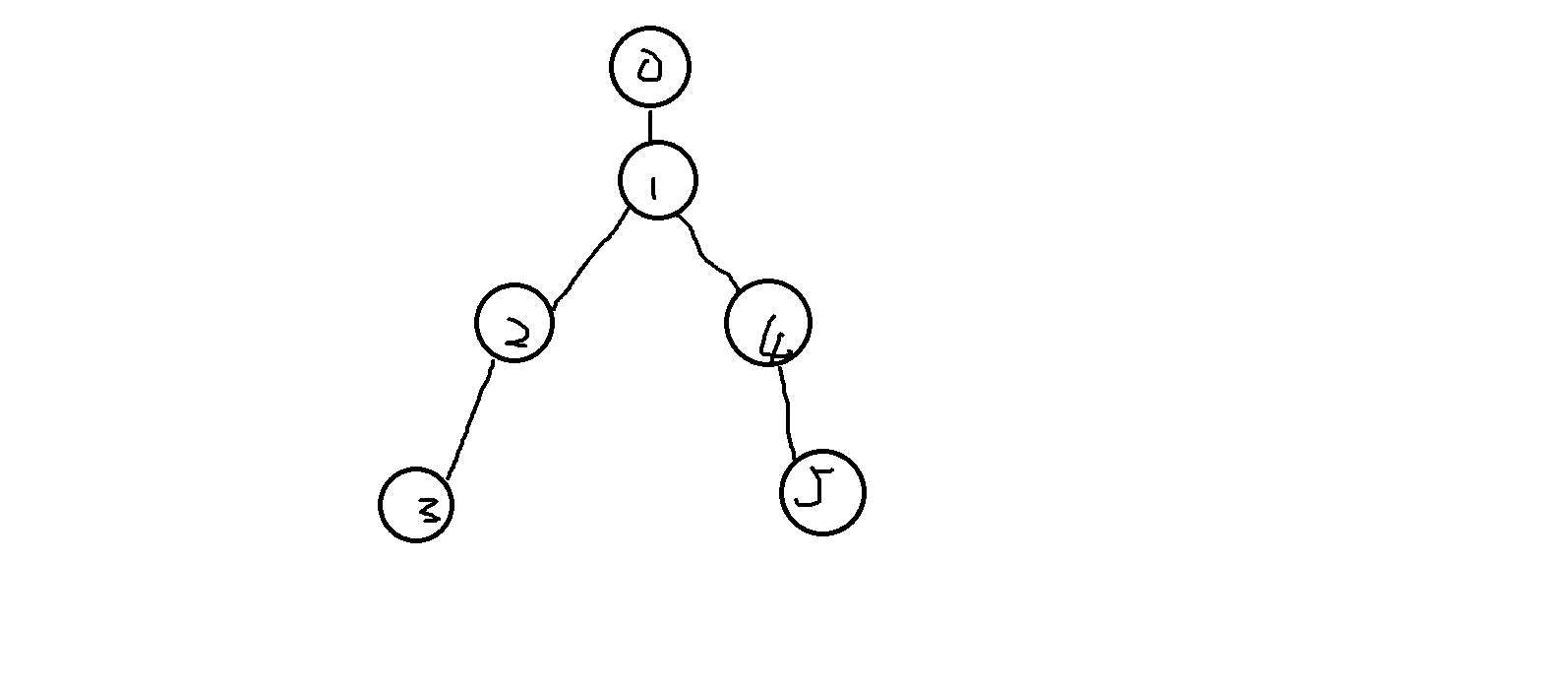
如果一个人要从 \(3\) 跑到 \(5\),那么如果在 \(2\) 点的观察员要满足 \(w[2] = dep[2] - dep[3]\),如果在点 \(4\) 的观察员要满足 \(w[4] = dep[fa[lca]] - dep[3] + dep[lca] - dep[4]\),简单来说就是如果处于 \(i\) 点的观察员可以观察到,那么要满足 \(w[j] = dep[j] - dep[a]\) 或 \(w[i] = dep[fa[lca]] - dep[a] + dep[lca] - dep[b]\),那么我们可以在点 \(a\) 至 \(lca\) 的链上打个为 \(dep[i] - dep[a]\) 标记,然后在 \(b\) 至 \(son[lca]\) 的链上打个为 \(dep[fa[lca]] - dep[a] + dep[lca] - dep[b]\) 的标记,然后用类似于差分和树上启发式合并即可
#include <bits/stdc++.h>using namespace std;const int N = 3e5 + 5;int n, m, w[N], s[N], t[N], dep[N], dp[N][25], ans[N], fa[N], lc[N];vector<int> g[N], sum[N];map<int, int> cnt[3][N];void dfs1(int u, int f) {dep[u] = dep[f] + 1;dp[u][0] = f;fa[u] = f;for (int i = 1; (1 << i) <= dep[u]; i++) {dp[u][i] = dp[dp[u][i - 1]][i - 1];}for (auto v : g[u]) {if (v == f) {continue;}dfs1(v, u);}
}int lca(int a, int b) {if (dep[a] > dep[b]) {swap(a, b);}for (int i = 20; i >= 0; i--) {if (dep[dp[b][i]] >= dep[a]) {b = dp[b][i];}}if (a == b) {return a;}for (int i = 20; i >= 0; i--) {if (dp[a][i] != dp[b][i]) {a = dp[a][i];b = dp[b][i];}}return dp[a][0];
}void dfs(int u, int f) {for (auto v : g[u]) {if (v == f) {continue;}dfs(v, u);for (auto p : {1, 2}) {if (cnt[p][v].size() > cnt[p][u].size()) {swap(cnt[p][v], cnt[p][u]);}for (auto cur : cnt[p][v]) {cnt[p][u][cur.first] += cur.second;}}}ans[u] = cnt[1][u][dep[u] + w[u]] + cnt[2][u][w[u] - dep[u]];
}int main() {cin >> n >> m;for (int i = 1, u, v; i < n; i++) {cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}dfs1(1, 0);for (int i = 1; i <= n; i++) {cin >> w[i];}for (int i = 1; i <= m; i++) {cin >> s[i] >> t[i];int lc = lca(s[i], t[i]);int dis = dep[s[i]] + dep[t[i]] - 2 * dep[lc];cnt[1][s[i]][dep[s[i]]]++;cnt[1][fa[lc]][dep[s[i]]]--;cnt[2][t[i]][dis - dep[t[i]]]++;cnt[2][lc][dis - dep[t[i]]]--;}dfs(1, 0);for (int i = 1; i <= n; i++) {cout << ans[i] << " ";}return 0;
}
Sum of Tree Distance
虚树和一个简单的树形 \(dp\) 即可,虚树就是建出一个 \(a_i\) 全部相同的数,这样就变得非常好处理
#include <bits/stdc++.h>using namespace std;#define int long longconst int N = 3e5 + 5;struct node {int v, w;
};int n, a[N], dep[N], dfn[N], dcnt, dp[N][25], ans, sz[N], stk[N], x, vis[N];vector<int> g[N], v[N];vector<node> new_g[N];void dfs1(int u, int f) {dfn[u] = ++dcnt;dep[u] = dep[f] + 1;dp[u][0] = f;v[a[u]].push_back(u);for (int i = 1; (1 << i) <= dep[u]; i++) {dp[u][i] = dp[dp[u][i - 1]][i - 1];}for (auto v : g[u]) {if (v == f) {continue;}dfs1(v, u);}
}int lca(int a, int b) {if (dep[a] > dep[b]) {swap(a, b);}for (int i = 20; i >= 0; i--) {if (dep[dp[b][i]] >= dep[a]) {b = dp[b][i];}}if (a == b) {return a;}for (int i = 20; i >= 0; i--) {if (dp[a][i] != dp[b][i]) {a = dp[a][i];b = dp[b][i];}}return dp[a][0];
}void dfs(int u, int f) {sz[u] = (a[u] == x);for (auto e : new_g[u]) {if (e.v == f) {continue;}dfs(e.v, u);sz[u] += sz[e.v];}
}void dfs2(int u, int f) {for (auto e : new_g[u]) {if (e.v == f) {continue;}ans += e.w * (sz[1] - sz[e.v]) * sz[e.v];if (u == 1) {//cout << e.w << " " << sz[1] << " " << sz[e.v] << "\n";}dfs2(e.v, u);}
}void clean(int u, int f) {sz[u] = 0;for (auto e : new_g[u]) {if (e.v == f) {continue;}clean(e.v, u);}new_g[u].clear();
}void build() {int top = 1;stk[top] = 1;for (auto cur : v[x]) {if (cur == 1) {continue;}int l = lca(cur, stk[top]);if (l != stk[top]) {while (dfn[l] < dfn[stk[top - 1]]) {new_g[stk[top - 1]].push_back({stk[top], abs(dep[stk[top - 1]] - dep[stk[top]])});new_g[stk[top]].push_back({stk[top - 1], abs(dep[stk[top - 1]] - dep[stk[top]])});top--;}if (dfn[l] > dfn[stk[top - 1]]) {new_g[l].push_back({stk[top], abs(dep[l] - dep[stk[top]])});new_g[stk[top]].push_back({l, abs(dep[l] - dep[stk[top]])});stk[top] = l;}else {new_g[l].push_back({stk[top], abs(dep[l] - dep[stk[top]])});new_g[stk[top]].push_back({l, abs(dep[l] - dep[stk[top]])});top--;}}stk[++top] = cur;}for (int i = 1; i < top; i++) {new_g[stk[i]].push_back({stk[i + 1], abs(dep[stk[i]] - dep[stk[i + 1]])});new_g[stk[i + 1]].push_back({stk[i], abs(dep[stk[i]] - dep[stk[i + 1]])});}dfs(1, 0);dfs2(1, 0);clean(1, 0);
}signed main() {cin >> n;for (int i = 1, u, v; i < n; i++) {cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}for (int i = 1; i <= n; i++) {cin >> a[i];}dfs1(1, 0);for (int i = 1; i <= n; i++) {if (!vis[a[i]]) {x = a[i];vis[x] = true;build();}}cout << ans;return 0;
}
Happy Life in University
我们可以先预处理初对于 \(i\) 节点来说的每个子树内的第一个与他 \(p\) 相等的 \(j\) 存在一个集合里,然后从下往上做操作,对于一个点 \(i\),先将他的集合内的数的子树都加上一个 \(-1\),然后将 \(i\) 的子树全部加上 \(1\) 即可
#include <bits/stdc++.h>using namespace std;#define int long longconst int N = 3e5 + 5;int t, n, a[N], tr[N * 4], lazy[N * 4], dfn[N], dcnt, sz[N], ans, cnt, b[N];vector<int> g[N], tmp[N];stack<int> stk[N];void pushdown(int i, int l, int r) {tr[i * 2] += lazy[i];lazy[i * 2] += lazy[i];tr[i * 2 + 1] += lazy[i];lazy[i * 2 + 1] += lazy[i];lazy[i] = 0;
}void modify(int i, int l, int r, int x, int y, int k) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i] += k;lazy[i] += k;return ;}int mid = (l + r) >> 1;pushdown(i, l, r);modify(i * 2, l, mid, x, y, k);modify(i * 2 + 1, mid + 1, r, x, y, k);tr[i] = max(tr[i * 2], tr[i * 2 + 1]);
}int query(int i, int l, int r, int x, int y) {if (l > y || r < x) {return 0;}if (l >= x && r <= y) {return tr[i];}int mid = (l + r) >> 1;pushdown(i, l, r);return max(query(i * 2, l, mid, x, y), query(i * 2 + 1, mid + 1, r, x, y));
}void build(int i, int l, int r) {if (l == r) {tr[i] = 0;lazy[i] = 0;return ;}int mid = (l + r) >> 1;build(i * 2, l, mid);build(i * 2 + 1, mid + 1, r);tr[i] = 0, lazy[i] = 0;
}void dfs1(int u, int f) {dfn[u] = ++dcnt;sz[u] = 1;if (!stk[a[u]].empty()) {tmp[stk[a[u]].top()].push_back(u);}stk[a[u]].push(u);for (auto v : g[u]) {if (v == f) {continue;}dfs1(v, u);sz[u] += sz[v];}stk[a[u]].pop();
}void dfs(int u, int f) {int maxi1 = 0, maxi2 = 0;for (auto v : g[u]) {if (v == f) {continue;}dfs(v, u);}for (auto cur : tmp[u]) {modify(1, 1, n, dfn[cur], dfn[cur] + sz[cur] - 1, -1);}modify(1, 1, n, dfn[u], dfn[u] + sz[u] - 1, 1);cnt = 2;b[1] = b[2] = 1;for (auto v : g[u]) {if (v == f) {continue;}int x = query(1, 1, n, dfn[v], dfn[v] + sz[v] - 1);b[++cnt] = x;}sort(b + 1, b + cnt + 1);ans = max({ans, b[cnt] * b[cnt - 1]});
}void Solve() {cin >> n;for (int i = 2, v; i <= n; i++) {cin >> v;g[i].push_back(v);g[v].push_back(i);}build(1, 1, n);for (int i = 1; i <= n; i++) {cin >> a[i];}dfs1(1, 0);dfs(1, 0);cout << ans << "\n";for (int i = 1; i <= n; i++) {g[i].clear();tmp[i].clear();}for (int i = 1; i <= n; i++) {while (!stk[i].empty()) {stk[i].pop();}}dcnt = 0;ans = 0;
}signed main() {ios::sync_with_stdio(0);cin.tie(0);cin >> t;while (t--) {Solve();}return 0;
}