Day1 介值定理

news/2024/11/19 21:30:11/文章来源:https://www.cnblogs.com/staring354/p/18432032

介值定理

设 $ f(x) $ 是 $ [l,r] $ 上的连续函数，且 $ f(l) \le f(r) $ ，则 $ \forall \ v \in [f(l),f(r)] \ , \exists \ u \in [l,r] \ , f(u)=v $

上午

思考题

有n个物品，每个物品有重量wi和体积vi且密度均匀。
你可以切物品，每次可以选一个物品切成两部分，也就是选一个0到1的实数k把物品分成k和(1-k)比例的两个物品。
你有最多X次切的机会。
问题1. 要想保证切完之后一定能把物品分成两组使得两组重量和相等，体积和也相等，X至少是几。
问题2. 设计高效算法求问题1的方案。
问题3. 如果是分成三组呢
问题0. 如果是要把物品分成两组使得两组数量相同且体积和也相等呢（不考虑重量）。

sol

问题1：
考虑将所有物品看作一个拼接在一起的圆环，每个物品所占环长与总环长之比等于其体积与总体积之比

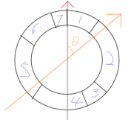
过圆心作一条直径，容易发现此时已满足平分体积的条件
考虑以垂直直径为标准，记 $ f(\theta) $ 表示标准直径绕圆心顺时针旋转 $\theta \ rad $ 后，逆时针方向的重量和减去顺时针方向的重量和的差
对于 $ f(0) $ 和 $ f(\pi) $ ，因为方向相反，显然互为相反数
此时存在介值定理，一定存在 $ 0 \le u \le \pi $ 满足 $ f(u)=0 $
取到零点时，最多划分掉两个物品，即2次划分一定有解

问题2：
考虑上述算法，旋转直径时只有 $O(n)$ 个分界点，每两个分解点之间的段均是一次函数，分讨一下即可做到 $O(n)$

问题3：
可以考虑先按上述算法分出 $1:2$ 的两部分，再将较大的部分分为 $1:1$

问题4：
还是考虑上述算法，此时 $f(\theta)$ 表示逆时针与顺时针的分界点个数之差
仍然存在介值定理，可套用上述算法求解

选题讲解

loj#560. 「LibreOJ Round #9」Menci 的序列

题目大意:
给定长为 $n$ 只包含 $+ \times$ 的操作序列 $S$ 和整数$k$，定义操作序列的权值如下：
初始变量 $res=0$ ，从前往后遍历操作序列，若当前操作是 $+$ 则 $res \leftarrow res+1 $ ，若当前操作是 $\times$ 则 $ res \leftarrow res \times 2 $ ，最后的权值为 $res \ mod \ 2^k $
求 $S$ 的子序列的最大权值是多少

sol

考虑初始时$res=0$，可以在操作序列前加上无限个$\times$
显然对于每个$+$，其对$res$的贡献为$2^c$，其中$c$表示子序列中这个$+$后面的$\times$的数量
注意到$\times++\ +$与$+\times+$实际上是等价的，因此可以得到每个$+$段长度不超过$2$的性质
记$c_i$表示新序列后面有$i$个$\times$的$+$个数
显然若$c_0 - c_{k-1}$均不为零，则$res=2^k-1$
否则找到最高的使得$c_{pos}=0$的位$pos$
高于$pos$的位都能取到$1$，低于$pos$的位因为$c_i \le 2$，进位最多到$pos$，显然全选
提交记录

下午

思考题

对一个序列a[1]...a[n]，找一个位置x，使得a[1]+...+a[x]和a[x+1]+...+a[n]的比值在[1/c,c]之间，要求c>=1尽可能小
问题1. c最大情况下是多少，并构造对应c的例子
问题2. 如果允许将某一个a[i]原位切开成两个相邻的位置，这两个位置的权值加起来是a[i]且任意分配，c最大情况下是多少，当n很大并且a[i]>=1的情况下，c会变小吗？
对一棵n个点的树，找一条边，使得这条边断开后，两边的连通子图的比值在[1/c,c]之间
问题3. c最大情况下是多少，并构造对应c的例子
问题4. 如果树是一棵二叉树，对任意一个给定的n，c最大情况下是多少，并给出一个通用的构造对应c的例子的算法
在树的基础上，如果给定一个结点x，将x删去后剩下若干个连通子图，将这些连通子图分成两组，使得两组点数的比值在[1/c,c]之间，要求c尽可能小
问题5. c最大情况下是多少，并构造对应c的例子
问题6. 如果结点x是你自己选定的，c最大情况下是多少，并构造一个通用算法

sol

问题1：
考虑极端情况$a=\{\inf,1\}$，显然此时$c=\inf$

问题2：
将$a_i$拆成$a_i$个大小为$1$的物品，此时从左到右扫描序列，每经过一个位置会使左部和右部的差增加$2$，根据介值定理显然左右之差能取到$\pm1$或$0$，极端情况下$c_{max}=2$，而随着$n$增大$c$的极限显然为$1$

问题3：
考虑菊花图，此时$c=\frac{1}{n-1}$

问题4：
二叉树即三度树，那么考虑构造一个点使得其三棵子树大小相同，此时删去任意边都有$c \le \frac12$

问题5：
对于任意树可以考虑将其三度化，每个点的左子节点是它的儿子，右子节点若还有不止一个的儿子则是权值为$0$的虚点，否则为剩余的儿子，类似左儿子右兄弟的三度化
此时任意树转成二叉树，使用问题4的结论即可

问题6：
同问题5

晚上

思考题

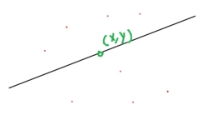
二维平面上有n个点，要求这些点互相不重合，并且三点不共线，编号为1...n，现在我们要画一条直线，如果一个点(x,y)满足Ax+By+C>=0，则视为点(x,y)在直线Ax+By+C=0的上方。将直线上方的点看做是一个集合。
问题1.如果n个点的坐标由你来构造，对直线Ax+By+C=0，假设A,B,C取遍所有实数，最多可以得到多少个不同的集合
问题2.如果有若干条直线，其上方点的集合相同，是否可以通过对这些直线进行旋转和平移，使得这些直线变成同一条直线
问题3.如果改变你在问题1中构造的点的坐标，不同的集合数是否会发生改变

问题4.给定点(x,y)，对于所有过(x,y)的直线，是否一定存在一条直线，使得直线两侧的点数最多只差1，这里的点数不统计(x,y)，如果点在直线上，由你决定属于哪一侧