前情概要
正三棱台的概念,表面积,体积公式,引申
动态演示
结合上图,你能说出正三棱台的各部分的名称吗?你能自行画出正三棱台的图形吗?
典例剖析
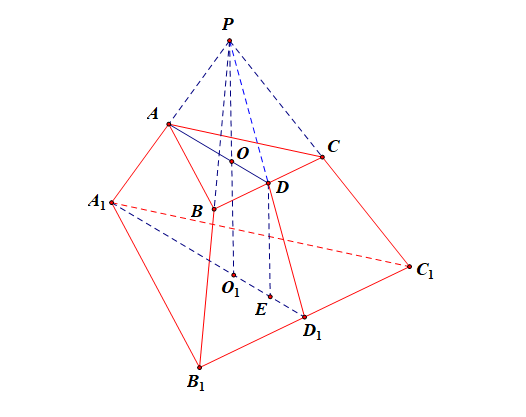
解:正三棱台的上下底面为正三角形,由正三角形的面积公式 \(S_{正\triangle}=\cfrac{\sqrt{3}}{4}a^2\),其中 \(a\) 为正三角形的边长,则由 \(\cfrac{\sqrt{3}}{4}a^2=\sqrt{3}\) 或 \(\cfrac{\sqrt{3}}{4}a^2=4\sqrt{3}\) ,可得上下底的边长分别为 \(2\) 和 \(4\),即 \(BC=2\),\(B_1C_1=4\),设上下底面的中心分别为点 \(O\) 和 \(O_1\),则 \(AD\) 和 \(A_1D_1\) 分别是上下底三角形的高线,连结 \(DD_1\),则 \(DD_1\) 是正三棱台的斜高,过点 \(D\) 作 \(DE\perp A_1D_1\) 于点 \(E\),则 \(D_1E\) 是斜高 \(DD_1\) 的投影;
由三角形的知识可知,\(OD=\cfrac{1}{3}AD\)\(=\)\(\cfrac{\sqrt{3}}{3}\),\(O_1D_1\)\(=\)\(\cfrac{1}{3}A_1D_1\)\(=\)\(\cfrac{1}{3}\times2\sqrt{3}\)\(=\)\(\cfrac{2\sqrt{3}}{3}\),则 \(D_1E=\cfrac{\sqrt{3}}{3}\),在 \(Rt\triangle DD_1E\) 中,由勾股定理可知 \(DD_1=\cfrac{\sqrt{39}}{3}\),
又正三棱台的侧面为等腰梯形, \(S_{BCC_1B_1}=\cfrac{(2+4)\times\frac{\sqrt{39}}{3}}{2}=\sqrt{39}\),
故该三棱台的表面积为 \(S=\sqrt{3}+4\sqrt{3}+3\times\sqrt{39}=5\sqrt{3}+3\sqrt{39}\),故选 \(A\) .
 正三棱台的相关知识点
正三棱台的相关知识点





![【泛微E9】修改表单字段类型,将[附件上传-上传文件]修改为[附件上传-上传图片]](https://img2024.cnblogs.com/blog/3476718/202409/3476718-20240926132244888-1877140924.png)