[ABC274G] Security Camera 3
给你一个 \(n\times m\) 的网格图,\(n,m\le 300\),每个空地上可以放任意多个任意方向的监控,一个监控视野覆盖对应方向最长连续空地,问监控覆盖所有空地最小化监控数量。
对于一个极长的连续空地,我们一定是在边边放置一个监控,而且两边是一样的,因此我们只需要考虑放置向右和向上的监控就行了。不需要考虑四个方向。
预处理出所有极长连续空地,一个连续空地我们只会放一个监控。问题变成最小化极长连续空地数量,使得覆盖所有空地。
显然一个方向的极长连续空地是互不相交的。因此对于每个空地,我们把它对应的横向极长连续空地和纵向极长连续空地连一条边,问题就是求二分图最小点覆盖(选择最少的点覆盖所有边)。显然这是一个二分图,选择一个点就是选择一个极长连续空地建一个监控。每个点必须被横向或者纵向的极长连续空地覆盖,所以就是最小点覆盖问题。
二分图最小点覆盖问题可以转化为网络流最大流问题。源点向所有横向的点连一条流量为 \(1\) 的边,所有纵向的点向汇点连一条流量为 \(1\) 的边,一个点属于编号为 \(x\) 的横向区间,同时属于编号为 \(y\) 的纵向区间,那么就连一条 \(x\to y\) 的流量为 \(1\) 的边。
其实中间连的那些边的流量不一定要设为 \(1\) 设为 \(inf\) 也可以。因为一个空地只会和两个极大块有关,所以最多只会有 \(1\) 的流量经过这条边。
做完啦!现在分析下时间复杂度。\(n,m\) 同阶,时间复杂度是 \(O(n^3)\) 的。
网络流点的数量是 \(O(n^2)\) 的,边的数量也是 \(O(n^2)\) 的。
时间复杂度证明参考 oiwiki。
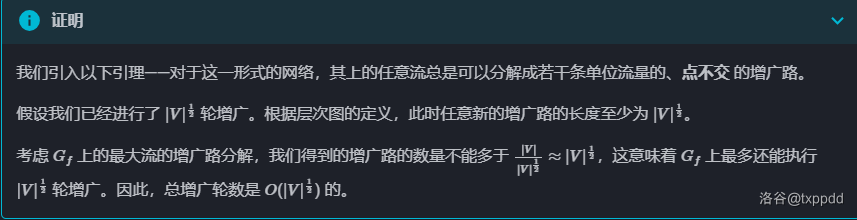
因此网络流的复杂度是 \(O(n^2\sqrt{n^2})=O(n^3)\)。
code
#include<bits/stdc++.h>
// #define LOCAL
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
using namespace std;
typedef long long ll;
const int N=305,inf=0x3f3f3f3f,M=N*N;
int n,m;
char c[N][N];
int id[2][N][N],s;
struct edge{int to,ne,f;
}e[M<<4];
int head[M<<4],cnt=1,cur[M<<4];
void addedge(int u,int v,int val){e[++cnt]={v,head[u],val};head[u]=cnt;
}
void adde(int u,int v,int val){addedge(u,v,val),addedge(v,u,0);
}
int S,T;
int dep[M<<4];
bool bfs(){queue<int> q;memset(dep,0,sizeof(dep));// memcpy(cur,head,sizeof(head));q.push(S);dep[S]=1;while(!q.empty()){int u=q.front();q.pop();cur[u]=head[u];// pf("u %d\n",u);for(int i=head[u];i;i=e[i].ne){int v=e[i].to,w=e[i].f;// pf("v %d\n",v);if(dep[v]!=0||w<=0) continue;dep[v]=dep[u]+1;q.push(v);}}// pf("%d\n",(int)dep[T]!=0);return dep[T]!=0;
}
int dfs(int u,int res){int flow=0;if(u==T||!res) return res;for(int &i=cur[u];i;i=e[i].ne){int v=e[i].to,w=e[i].f;if(dep[v]!=dep[u]+1||!w) continue;int fl=min(res,w);int x=dfs(v,fl);if(x==0) dep[v]=-1;res-=x,flow+=x;e[i].f-=x,e[i^1].f+=x;}return flow;
}
int dinic(){int flow=0;while(bfs()) flow+=dfs(S,inf);return flow;
}
int main(){#ifdef LOCALfreopen("in.txt","r",stdin);freopen("my.out","w",stdout);#endif sf("%d%d",&n,&m);rep(i,1,n){sf("%s",c[i]+1);}S=1,T=2;s=2;rep(i,1,n) {rep(j,1,m) {if(c[i][j]=='.'){if(id[0][i][j-1]) id[0][i][j]=id[0][i][j-1];else s++,id[0][i][j]=s,adde(S,s,1);}}}rep(j,1,m) {rep(i,1,n) {if(c[i][j]=='.'){if(id[1][i-1][j]) id[1][i][j]=id[1][i-1][j];else s++,id[1][i][j]=s,adde(s,T,1);}}}rep(i,1,n){rep(j,1,m){if(c[i][j]=='.') adde(id[0][i][j],id[1][i][j],1);}}pf("%d\n",dinic());
}