打得非常好的一场比赛,所以才来写总结。
T1 「SMOI-R1」Queue
打表找规律题,太签到了,不讲。
T2 「SMOI-R1」Company
首先,如果要使得 \(x,y\) 的距离最后是尽可能远的,我们就要考虑一些满足最优解的性质。
不难想到一个结论:如果将初始时每一棵树缩成一个节点,那么最优解形成的新的树必然是一条链,且链的两端分别是初始的第 \(1,2\) 棵树。因为只有这样才能保证每一棵树都对答案产生了影响,否则说明必然存在一棵树是对 \(x,y\) 的距离毫无影响的。下文记 \(t_i\) 表示初始第 \(i\) 棵树。
由于初始每棵树都有根,且题中的连边方式是让叶子节点与树根连边,也就是说最终形成的树也一定是一个有根树。我们不妨来探讨一下这个树根:
-
如果树根为 \(t_1\) 或者 \(t_2\),这就很显而易见了。假设现在树根为 \(t_1\),那么就说明树中最深的节点就是 \(t_2\)。我们记录一个当前节点下标 \(j\),初始时 \(j=x\),每次我们找到 \(j\) 所在的树 \(t_i\) 中距离 \(j\) 最远的一个叶子节点 \(j\prime\),接着让 \(j\) 移动到 \(j\prime\) 处,这个时候我们再考虑跳到另一个树的根上。总的来说,我们到达的树的先后顺序是 \(1\to (3\to 4\to\dots\to n)\to 2\),括号中的可以任意改变顺序。因此,对于所有 \(i>2\) 的 \(t_i\),\(j\) 在其中移动的距离一定是树的深度;对于 \(t_1\),\(j\) 移动的距离是 \(x\) 到某一个叶子节点的最远距离;对于 \(t_2\),\(j\) 移动的距离则是 \(y\) 的深度。计算此类情况的答案时,只需要计算它们的和就行了。
-
如果树根不是 \(t_1\) 或者 \(t_2\),则说明 \(j\) 的移动方向是先往上,后往下。我们考虑枚举这个树根 \(t_k\)(\(k>2\))。由于 \(j\) 在除了 \(t_1,t_2,t_k\) 以外的所有树中经过的距离都是其深度,所以这些树的排放并不重要。而对于 \(t_1,t_2\),\(j\) 的其中移动的距离分别是 \(x,y\) 在树中的深度;对于 \(t_k\),由于它肯定是选择了两个叶子节点进行连边,所以 \(j\) 在其中移动的最大距离就是最远的两个叶子节点之间的距离。由于枚举的时间复杂度是 \(O(n)\),我们记 \(d_i\) 表示第 \(i\) 棵树的最大深度,然后计算 \(sum=\sum_{i=3}^n d_i\),每次计算除了 \(t_1,t_2,t_k\) 之外的树的总代价时,我们只需要用 \(sum\) 减去 \(d_k\) 就行了。
综上,对于 \(t_1,t_2\),我们要计算 \(x,y\) 在其中的深度以及 \(x,y\) 到达某个叶子节点的最长距离。对于 \(t_i\)(\(i>2\)),我们要计算 \(d_i\) 以及其中最远的两个叶子节点的距离。然后按照上述方法计算就行了。
但是要注意,树与树之间的连边也会计入答案。考虑到最终的树的组成形态,我们可以知道一共会添加 \(n-1\) 条边,并且它们都会计入 \(x\to y\) 的最长距离。
T3 「SMOI-R1」Game
首先有一个非常常规的思路:枚举每一个数,求出其作为最大值的区间个数。这道题也是如此。
如果最终的序列 \(a\) 长度够小,那么我们可以利用单调栈得出每一个数 \(a_i\) 向前和向后的第一个 \(>a_i\) 的数 \(a_{l_i}\) 和 \(a_{r_i}\),如果找不到则分别为 \(0,|a|+1\),那么 \(a_i\) 作为最大值的区间就有 \((i-l_i)(r_i-i)\) 个。
但是需要注意,有的区间是会被算重的,比如 \(a=\{1,2,1,2\}\),两个 \(2\) 分别计算得到的区间都包含 \([2,4],[1,4]\)。这个时候考虑更改 \(l_i\) 的定义为向前找到的第一个 \(≥a_i\) 的数的下标,如果找不到则为 \(|a|+1\),计算方式仍然是 \((i-l_i)(r_i-i)\)。这样就可以保证不会重复计算了,原因显然,因此把它当成一个 Trick 掌握就行了。
但是出题人非常可爱啊!这个 \(a\) 的长度可以达到 \(10^{15}\),不可能直接计算。但是 \(n\) 的范围倒是很合理。这就说明我们要找到 \(a\) 序列的计算规律。
我们将 \(a\) 视为 \(n\) 个形如 \(\{1,2,\dots,b_i-1,b_i\}\) 的子段前后拼接得到的序列,记 \(s_{i,j}\) 表示第 \(i\) 个子段中的第 \(j\) 个数在 \(a\) 中的下标。
先考虑 \(s_{i,b_i}\) 的代价该怎么计算。由于各个子段的单调性,我们可以知道其向前能够找到的第一个 \(≥b_i\) 的数的下标一定是 \(s_{j,b_j}\)(\(j<i\)),向后能够找到的第一个 \(> b_i\) 的数的下标一定是 \(s_{k,b_i+1}\)(\(i<k\),注意是 \(b_i\) 而不是 \(b_k\))。可以发现 \(b_j\) 是 \(b_i\) 向前第一个大于等于它的数,\(b_k\) 是 \(b_i\) 向后第一个大于它的数。可以通过这个结论,利用单调栈找到 \(j,k\)。我们找到这两个 \(j,k\) 记为 \(L(i),R(i)\)(如果不存在满足条件的 \(j\) 或 \(k\),则分别变为 \(0,n+1\)),则 \(s_{i,b_i}\) 的区间个数就是 \((s_{i,b_i}-s_{L(i),b_{L(i)}})(s_{R(i),b_{i}+1}-s_{i,b_i})\),可以利用 \(b_i\) 的前缀和解决。
我们记 \(sum_i=\sum _{j=1}^ib_j\),那么:
每一个子段的顶点值我们就算完了,我们考虑将这种做法拓展到其它数上面。其实我们可以利用图像去思考:
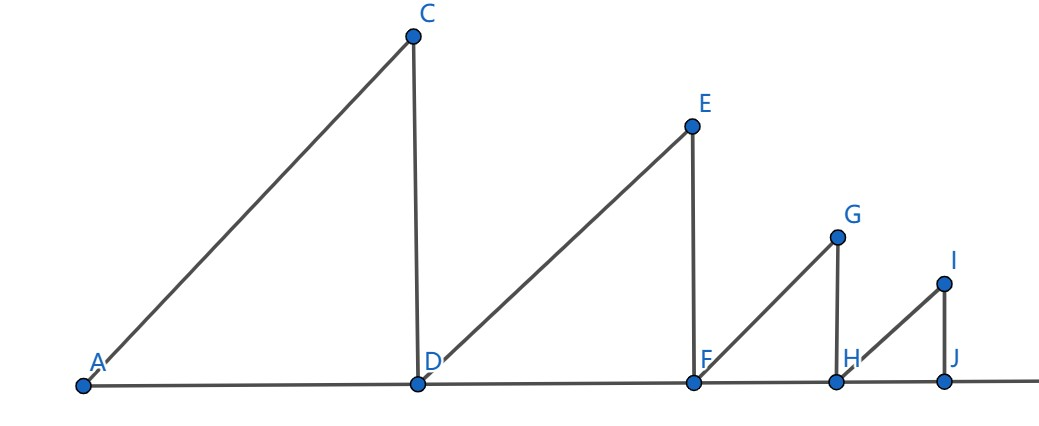
我们知道对于每一个数,要去找前面和后面比自己大的,由于除了顶点以外,每个数的后面都有一个比自己大一的数,所以右侧比较好找。而对于左侧,我们结合上图去思考,不难发现最终形成的 \(a\) 序列就是若干个等腰直角三角形排在一起,那么每个数作为最大值的区间可以延展到的左端点一定是在 \(s_{k,b_k}\) 的位置。因此我们像之前那样用一个单调栈就行了。
但是对于每个数都用单调栈的话显然会寄。
我们可以找一下规律:
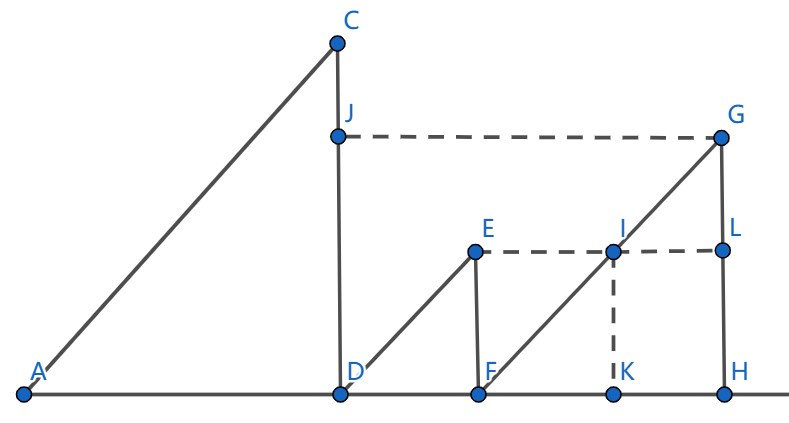
考虑对第 \(3\) 个子段的每个元素的答案进行统计,我们发现 \(IK\) 这一段对应过去的线段是 \(EF\),这说明 \(1\leq j\leq |IK|\) 的元素 \(s_{3,j}\) 可以向左延伸的最远点都是 \(F\),即 \(s_{2,b_2}\)。而 \(GL\) 对应过去是 \(CD\) 的一个子线段,这说明 \(|IK|<j\leq |GH|\) 的元素 \(s_{3,j}\) 向左延伸的最远点都是 \(s_{1,b_1}\)。这启示我们将每一个子段中的元素分成若干个子部分进行处理,并且要保证每个部分的 \(s_{i,j}\) 对应的左侧端点是相同的。
于是我们用单调栈去储存 \(b_i\),维护一个单调递减的子序列的下标。当我们要处理第 \(i\) 个子段时,我们就在栈中从后往前遍历,设当前遍历的元素为 \(p\),上一个遍历的元素是 \(q\),那么我们就将 \([s_{i,b_q+1},s_{i,b_p}]\) 的答案进行加和,下文令 \(t=sum_{i-1}-sum_p+b_q\),\(m=b_p-b_q\),则:
这样就可以 \(O(1)\) 计算这一段的答案之和了。
根据单调栈的性质,可以推断 \(n\) 个子段分成的子部分的个数和是 \(O(n)\) 级别的,可以跑过。
T4 「SMOI-R1」Apple
听网友说是个 CF 里面经典的 Trick,但是我不知道,不然我应该可以拿 \(10\) 块钱了。。。
不过不要慌,只要我现在会了就行。
对于这种进制上的子集问题,我们难以使用线段树这一类树形数据结构进行维护,所以我们可以考虑这样一个 Trick:对于一个 \(2^n\) 不可过但是 \(2_{\lfloor \dfrac{n}{2}\rfloor}\) 可过的题,我们把所有进制位分为前 \(\lfloor \dfrac{n}{2}\rfloor\) 位和后 \(n-\floor \dfrac{n}{2}\rfloor\) 位,然后对左半边的 \(2^{\lfloor \dfrac{n}{2}\rfloor}\) 个状态维护信息。
由此,我们设 \(sum_i\) 表示 \(i\) 的子集中,所有右半边与 \(i\) 相同的状态 \(j\) 的权值之和。那么对于每次的修改操作,如果是对状态 \(i\) 进行修改,则我们找到所有满足 \(i\subseteq j\) 且 \(i,j\) 右半边相同的状态 \(j\),然后对 \(sum_j\) 进行修改,由于右半边固定,我们只需要枚举左半边,这样每次的时间复杂度就是 \(O(2^{\lfloor \dfrac{n}{2}\rfloor})\)。对于每次的询问操作,我们就找到所有满足 \(j\subseteq i\) 且 \(i,j\) 左半边相同的状态 \(j\),然后对所有的 \(sum_j\) 进行加和,由于左半边固定,我们只需要枚举右半边的子集,这样每次的时间复杂度就是 \(O(2^{n-\lfloor \dfrac{n}{2}\rfloor})\)。
因此总时间复杂度就是 \(O(q2^{\dfrac{n}{2}})\)。
整体来说,感觉和 meet in the middle 的结构是差不多的,都是做到了把时间复杂度上的指数减少一半。