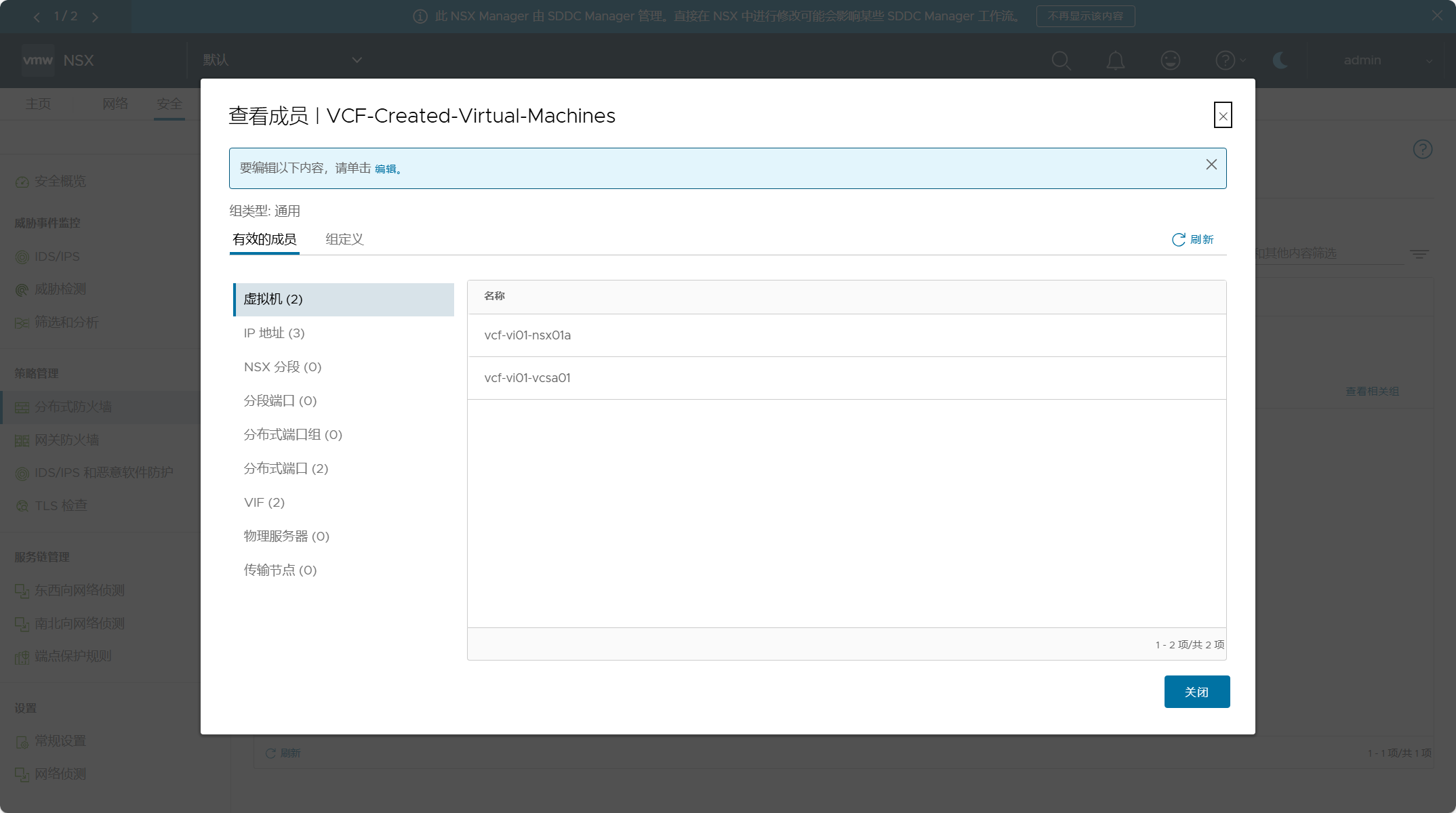
在博弈论中,纳什均衡(Nash Equilibrium)是博弈各方的一种策略组合,在这个组合下,每个参与者的策略都是对其他参与者策略的最优反应。换句话说,在纳什均衡下,任何一方都没有动机单方面改变自己的策略,因为那样做不会带来更高的收益。然而,纳什均衡的稳定性问题引发了大量的研究。特别是当我们考虑到现实中的人们有时会“犯错”或者随机地偏离最优策略时,传统的纳什均衡可能显得不够稳定。为了解决这个问题,颤抖手纳什均衡(Trembling Hand Perfect Nash Equilibrium)应运而生,它通过允许博弈参与者有一定概率选择非最优策略,从而增强了纳什均衡的稳定性。
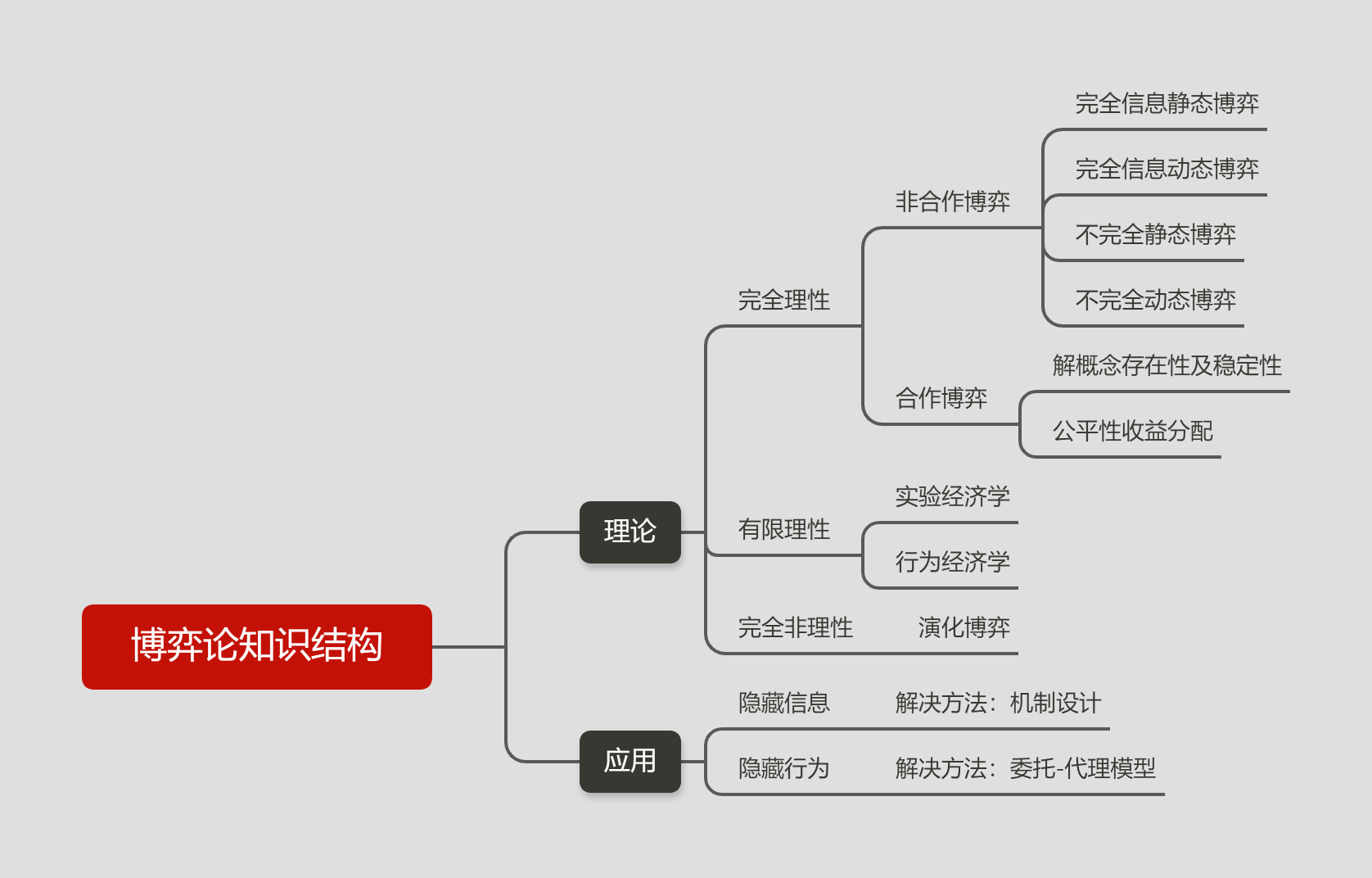
一、颤抖手博弈纳什均衡
“颤抖手精炼均衡”概念是泽尔腾提出的对纳什均衡的一个改进。在任何一个博弈中,每个局中人都有一个犯错误的可能性(类似一个人用手抓东西时,手一颤抖,他就抓不住他想抓的东西)。一个策略对是一个颤抖手精炼均衡时,它必须具有如下性质:各局中人\(i\)要采用的策略,不仅在其他局中人不犯错误时是最优的;而且在其他局中人偶尔犯错误(概率很小,但大于0)时还是最优的,可知颤抖手精炼均衡是一种较稳定的均衡。为了解决纳什均衡的稳定性问题,诺贝尔经济学奖得主 Reinhard Selten 提出了颤抖手纳什均衡(Trembling Hand Perfect Nash Equilibrium)这一概念。这个均衡考虑了现实中决策者可能会犯错的情况,即参与者以极小的概率选择非最优策略。通过允许每个参与者的手“颤抖”一下,理论能够更稳健地描述现实决策过程中的均衡。
1.2 颤抖手均衡的定义
颤抖手纳什均衡是纳什均衡的一种加强形式,它要求每个参与者的策略对手的颤抖(即他们选择非最优策略的极小概率)具有鲁棒性。具体来说,在颤抖手均衡中,参与者即使面对对手可能颤抖的情况,也必须选择能最大化其期望收益的策略。
设想一个博弈中每个参与者都可能以极小的概率“犯错”,即以某个\(\epsilon> 0\) 的概率偏离最优策略。这时,参与者不能仅仅选择那些在某些情况下有更高回报的策略,而是必须选择在所有可能偏离情形下都能保证最优收益的策略。
1.2 颤抖手均衡的形式化
假设一个博弈中有\(n\)个参与者,每个参与者\(i\)选择策略\(s_i\)的概率为 \(p_i(s_i)\),并且存在一个很小的概率\(\epsilon_i\)表示参与者\(i\)选择“非最优策略”的概率。颤抖手纳什均衡要求在每个参与者的策略中,任意小的\(\epsilon_i\) 偏差下,博弈的均衡解仍然保持稳定。也就是说,当\(\epsilon_i \to 0\)时,参与者的策略选择应该收敛于一个纯策略纳什均衡。
例1:
| 博弈方1\博弈方2 | L | R |
|---|---|---|
| U | 10,0 | 6,2 |
| D | 10,1 | 2,0 |
因为从这个策略组合出发,不管博弈方2是否有偏离R的可能,博弈方1都没有必要偏离U;对博弈方2来说,虽然博弈方1从U偏离为D对他的利益有不利的影响,但只要博弈方1偏离的可能性不超过2/3,那么自己改变策略并不合理。在这个博弈中(D,L)和(U,R)都是纳什均衡,其中(D,L)对博弈方1较为有利,(U,R)对博弈方2较为有利。
在不考虑选择和行为偏差的情况下,这两种纳什均衡都是稳定的。如果考虑到博弈方的选择和行为可能出现的偏差,具有稳定性的概率较大的均衡来说,我们称之为颤抖手均衡。
假设博弈方的策略能选择颤抖手均衡。那么博弈方1选择U,进而博弈方2选择R,这是选择颤抖手均衡的结果。
我们把上面这个博弈中博弈方1的得益情况做少量改变,颤抖手均衡的情况就会发生变化。我们看下图的得益矩阵情况:
| 博弈方1 \ 博弈方2 | L | R |
|---|---|---|
| U | 9,0 | 6,2 |
| D | 10,1 | 2,0 |
我们发现前一个博弈中的非颤抖均衡(D,L),变成了后一个博弈中的颤抖手均衡,因为现在即使博弈方1仍然会考虑博弈方2偏离L而错误选择R的可能性,但只要这种可能性确实很小(即不超过1/3),那么博弈方1坚持选择D而不选U是最佳策略,因此该博弈中有两个颤抖手均衡。假设博弈方2偏离L的概率为a,那么不偏离的概率为1-a,则(1-a) = 2a,得到a = 1/3**。
通过这两个例子的对比可以看出,一个策略组合要是一个颤抖手均衡,首先必须是一个纳什均衡,其次是不能包含任何“弱劣策略”,也就是偏离对偏离者没有损失的策略。包含“弱劣策略”的纳什均衡不可能是颤抖手均衡,因为它们经不起任何非完全理性的“扰动”,缺乏在有限理性条件下的稳定性。
二、颤抖手纳什均衡
颤抖手纳什均衡(Trembling Hand Nash Equilibrium)是对传统纳什均衡的扩展,它引入了博弈者偶尔可能犯错误的情况。颤抖手纳什均衡不仅要求每个参与者的策略在面对对手的最优策略时是最优的,还要求即使对手偶尔出错,这种均衡策略也要具备稳定性。
在经典纳什均衡中,博弈者会假设其他博弈者完全理性,并且所有博弈者都会严格按照最优策略进行选择。然而,在实际决策过程中,博弈者可能会由于各种原因偶尔出错,即他们可能会选择并非最优的策略。为了应对这种可能性,颤抖手纳什均衡提出了一种更稳健的策略选择方式,要求参与者在对手可能偶尔选择“错误”策略时,也能采取相对最优的策略回应。简言之,颤抖手纳什均衡强调了稳健性。它不仅要求每个博弈者的策略在面对理性对手时是最优的,还要在对手偶尔“颤抖”选择非最优策略时,这个策略仍然能保证参与者的最大收益。
例2:考察下面例子中所有纳什均衡
| Player1\Player2 | $$L(q_1)$$ | $$C(q_2)$$ | $$R (1-q_1-q_2)$$ |
|---|---|---|---|
| \(T (p_1)\) | 0,0 | 0,0 | 0,0 |
| \(M (p_2)\) | 0,0 | 1,1 | 1,1 |
| \(B\) | 0,0 | 0,2 | 2,2 |
画线法找到所有PNE: (T, L), (M, C), (B, R)。无差异方法找到MNE:
结合\(q_1 + q_2 + q_3/2 = 1\) 得到\(q_1 = 0, q_2 = 2/3, q_3 = 1/3\),此时 player2 也为 C, B 间的混合策略。
则为了保证\(v_2(C) = v_2(R)\), 令:
检查: 由于\(BR_2(B) = 2/3, BR_1(q_2 = 2/3, q_3 = 1/3)\)得 \(\{p_2 + p_3 = 1\}\),则 \((B, 2/3C + 1/3R)\)为混合策略纳什均衡。
注意到,三个纯策略纳什均衡 (T, L), (M, C) 线下两个均衡更为稳健:
考虑 player1 的选择\(T, L\) 由 \(T, L\) 此时对手偏离 L 而选择 R 仍能保持同样的收益(但不能提高,否则违反纳什均衡)。则这种偏离导致\(T\) 不再是 player1 的最优反应;
考虑 player1 的选择 \(B, R\) 时的\(B\),此时对手偏离 R 而选择 C 仍能保持同样的收益(但不能提高,否则违反纳什均衡)。
则这种偏离致使 B 不再是 player1 的最优反应。即对于 player1,对比每行收益,排除均衡所在的对手策略(分别是 L, R 行与 B 行都在对手剩余策略下“弱势”于其他己方策略(用坚线标出),可以理解为对手故意让人后悔。
例3: 考察下面投票博弈中的所有纳什均衡
奇数个评委票,所有 N 候选人中选出一个。评委有两个选择:保留现任 (Q) 和更换现任 (A),保留和更换与否取决于多数人的决定。所有人都认为更换更好。
该博弈中存在多个纳什均衡。其中两个极端的均衡是:所有人选择 Q 和所有人选择 A。考察 3 个评委的情况:
| Player3 选择 Q | Q | A |
|---|---|---|
| Q | 0,0; 0,0 | 0,0; 0,0 |
| A | 0,0; 0,0 | 1,1; 1,1 |
注意到 3 个人时仅有 1 人选择 Q 和所有人选择 A 两种纳什均衡。而所有人选择 A 之所以成为纳什均衡,是因为单个评委的选择无法影响整体投票结果(没有人是 pivotal),比如在评委1的视角,任何策略只会导致 (A, Q; Q)。
但是显然,一旦有人偏离\(A, Q; Q\),比如评委2偏离导致\(A, Q; Q\) 则评委1b 应选择改变。显然,这也显现出去除所在的对手策略\(A, Q; Q\) 后,弱势于 3 导致的不稳定。
综上,聪明的参与人应当不会选择一个对手行为偏离的均衡中“弱势”的策略,此外对手引入正解标准偏离的均衡纳什均衡时,参与人原有均衡策略不再是最优反应。因此,我们需要从纳什均衡中精炼出更稳健的方案: 鼓励斗争精炼均衡。
综上, 足够聪明的参与人应当不会选择一个在对手行为偏离纳什均衡时"弱劣"的策略, 即当对手以正概率偏离纳什均衡策略时, 参与人原纳什均衡策略不再是最优反应. 因此, 我们需要从纳什均衡中精炼(refine)出更稳健的子集: 颤抖手精炼均衡
三、案例
在演进博弈论中,颤抖手均衡尤其具有解释力。演进博弈论研究的是博弈双方通过一系列重复博弈形成的稳定策略,这种稳定性不一定来源于完全理性的策略计算,而可能是一种随机形成的过程。在这一过程中,博弈者会基于对对方行为的观察与猜测,逐步调整自己的策略,从而形成一种稳定的均衡。颤抖手均衡则解释了即使在对手偶尔出错的情况下,稳定的策略仍然能够维持。要将一种均衡定义为颤抖手纳什均衡,必须满足以下两个关键条件:
策略的最优性:即使考虑到对手有可能颤抖(选择非最优策略),每个博弈者的策略仍然是最优的。换句话说,颤抖手纳什均衡不仅考虑了传统意义上的理性选择,还加入了应对不确定性和微小错误的策略。
策略的鲁棒性(稳健性):在对手可能犯错的情境下,参与者的策略依然能为其带来最大利益。这一特征确保了颤抖手纳什均衡相比于传统纳什均衡更具稳定性和鲁棒性。

一个博弈有可能存在很多个纳什均衡,对纳什均衡的精炼就是以不同的标准剔除在某一衡量标准下相对不合理或不稳定的纳什均衡而筛选出最合理或稳定的纳什均衡, 这个过程叫做纳什均衡的精炼(refinement)。颤抖手均衡是纳什均衡的一种精炼, 简单地说, 在一个纳什均衡状态,如果其中一个参与者的手颤抖了一下(假设为小概率事件)选择了次优的策略,那么一个纳什均衡是颤抖手均衡的要求就是参与者有动机重新回到原来的均衡,而不是这个偏离并趋向另一个纳什均衡。 如上图的例子, 图1显示这个博弈有两个纯策略纳什均衡,(A, A) 和 (B,B), 收益分别是 (1,1) 和 (2,2) ;但颤抖手均衡只有一个,就是(A, A),收益为(1,1)。解释如下:
假设双方处于(A, A)这个纳什均衡, 如果参与者 I 颤抖,选择了B, 那么博弈的结果是 (B, A),在 (B, A), 参与者 I 有动机改变现状,因为选B的收益是0, 而选A的收益是1, 所以参与者 I 会重新选择A, 使博弈回到(A, A)这个均衡,对参与者 II 来说,(B,A)和(B,B)的收益是一样的,都是2,所以在(B,A)参与者II 没有动机改变现状。综上, 在(A,A)这个均衡,颤抖后博弈会重新回归这个均衡。直观地说(A,A)是抗震的,震完以后会归位。(A,A)就是一个颤抖手均衡。
相反,(B,B)就不是一个颤抖手均衡。
假设双方处于(B,B), 收益 (2,2),如果有参与者颤抖,比如参与者II 颤抖到A,博弈结果成为(B, A),收益变成 (0,2),在这个情况下,对于II 来说没有动机改变,因为颤抖前后收益都为2, 但对于I 来说,就不一样了,如果II 颤抖到A, I 的收益就从2变到0, 如以上所述,在(B,A)的情况下,I 有动机改变并选A。 所以,在(B,B)这个纳什均衡点,颤抖后均衡会趋向 (A,A)这个点,所以(B,B)就是在颤抖情况下不稳定的, (B,B)就不是一个颤抖手均衡。
在只有两个参与者的情况下,颤抖手均衡的一个充分必要条件是:是纳什均衡并且没有一个参与者的策略是弱劣策略(weakly dominated)。如图的列子里,B 对双方来说都是弱劣策略,所以根据这个充要条件,(B,B)可以被简单地剔除。
总结
颤抖手纳什均衡(Trembling Hand Perfect Nash Equilibrium)是博弈论中对传统纳什均衡的扩展和加强。传统纳什均衡假设所有参与者都理性地选择最优策略,但在实际中,参与者可能会由于错误或其他不确定因素,偶然地选择非最优策略。颤抖手均衡通过引入参与者可能出现的“颤抖”——即轻微的非理性行为或策略偏离,从而使均衡在面对这种偶然“错误”时仍然保持稳定。换句话说,这一均衡要求策略不仅在当前情境下最优,而且在对手可能犯错的情况下也依然是最优的。
相比普通的纳什均衡,颤抖手纳什均衡更加现实,因为它考虑了策略选择中的微小偏差,并确保均衡解在各种细微扰动下仍然成立。特别是在存在多重均衡的博弈中,颤抖手均衡可以帮助筛选出更稳健的解,从而避免因策略偏差导致的不稳定现象。它不仅广泛应用于经济学中的市场进入博弈、拍卖博弈等,还在进化博弈论中用于解释物种如何形成稳定的行为策略。因此,颤抖手纳什均衡为博弈论提供了一个更强的稳定性标准,它在面对具有多重均衡和不完全信息的博弈时,提供了更为精确的分析工具。
参考文献
1.博弈论新讲(5) 颤抖手精炼均衡
2.【博弈论笔记】第三章完全且完美信息动态博弈
3.完全信息动态博弈与子博弈完美纳什均衡