1. 绪论
在真实的业务场景中,时间序列数据具有以下特点:
- 采集频率(秒级甚至毫秒级)高,导致数据量非常庞大。
- 数据价值密度低。
对数据进行合理的降采样不仅极大地可以降低系统压力、节约存储成本,同时也可以帮助用户聚焦重要信息,提升数据价值。本教程将以要点感知算法为例介绍如何在 DolphinDB 自定义并应用算法降采样数据。
1.1 行业背景
在物联网用户场景中,有一个普遍的需求是需要查询某个采集点的全年(一季度、一个月)的数据并做展示分析。在展示时,如果显示所有数据,会有性能问题,特别是实时展示。同时,这个也不是必须的,因为只需要展示大概的趋势就足以达到决策要求,太多数据点反而可能模糊决策。以折线图为例,可视化场景中,当 x 轴的数据不断增多,对应 y 轴的数据量增多,体现在图上的折线就会变得越来越复杂,当数量达到一定程度,很难再通过图找到具体的某一个点所表述的真实值是什么,数据变得很拥挤。下图展示了 1 个包含 1 万个数据点的折线图:
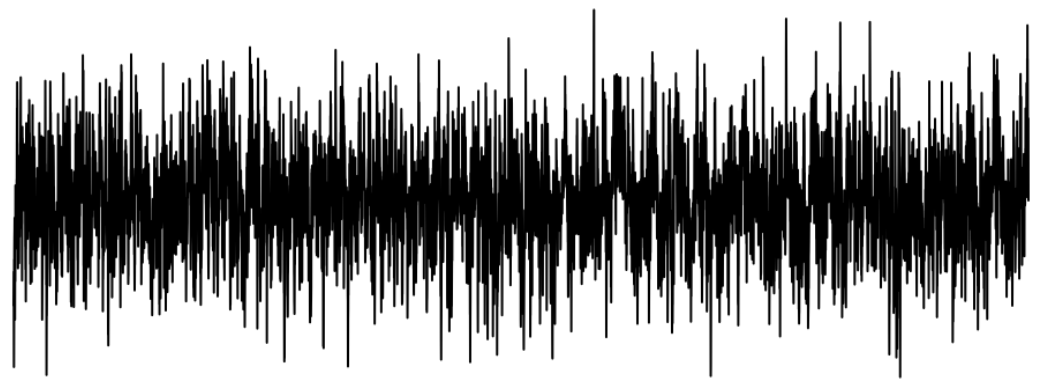
为了能够看到图形的整体,我们就要隐藏一些点,仅展示那些能够代表其他的点,或者是创建能够代表这些点的新数据点,这就是降采样算法解决的问题。
1.2 业务挑战
总体而言,在上述物联网时序数据应用场景中,首先需要将数据存下来,再将一定时间跨度的数据进行可视化展示,或者是流计算实时推送数据进行展示,而不对数据进行降采样,会存在以下几个问题:
- 存储成本:高采集频率、多采集点数据的存储成本极高
- 数据展示:展示原始数据遭遇性能瓶颈,且大量噪声数据影响局部趋势
- 数据价值:数据价值不与存储、展示成本成正比
2. 降采样算法概述
DolphinDB 已经内置实现了简单的降采样算法如最大值、最小值、平均值等,用户可以直接调用相应函数进行计算。上述降采样算法都是将多条数据用一个值进行表示,这种表示方法的优点是计算简单、快速,缺点是信息损失较大。除此之外,许多学者还提出了大量更为复杂、高级的降采样算法,适用于不同的场景。DolphinDB 的语言具有强大的编程能力,支持用户自定义实现复杂的降采样算法,本文接下来将以 PIP 算法为例,介绍其算法原理、DolphinDB 脚本实现,并且给出了案例脚本,用户可以在自己的 DolphinDB server 上直接运行该脚本。
3. PIP 算法
3.1 PIP 介绍
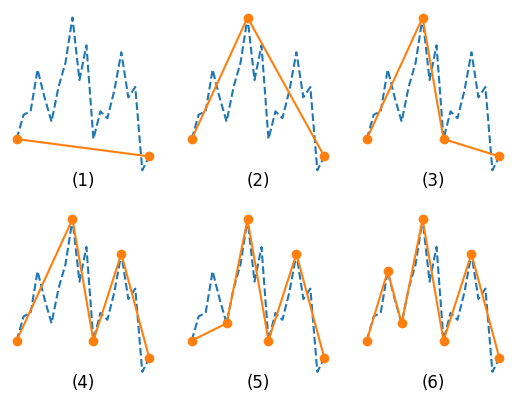
PIP(Perceptually Important Points)算法又叫要点感知算法,是一种时间序列聚合算法,其思路是:对于一个长度为 n 的时间序列数据,迭代地依据最大距离原则采样出 k 个数据点, k 是人为设置的降采样数据点数(k <= n)。PIP 算法的具体步骤如下(论文参考:https://sci-hub.se/10.1109/iscmi.2017.8279589 )
- 第一步:采样出时间序列的第 1 个和最后 1 个样本放入降采样数据点集
- 第二步:计算剩余未采样样本点到其邻接的 2 个要点构成的直线的距离
- 第三步:采样出距离最大的样本点放入降采样数据点集
- 第四步:重复第二步和第三步直到采样要点数达到 k 个
可以通过下面的演示图片,更直观的感受 PIP 算法的计算过程:
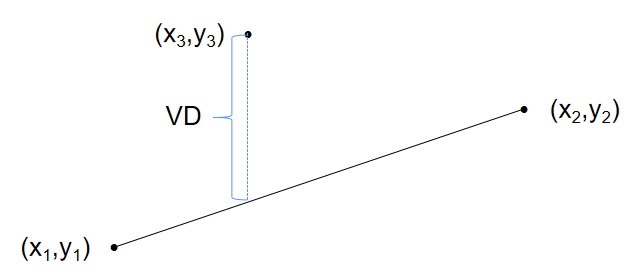
其中,上述点到直线的距离计算常用的是垂直距离(Vertical Distance),本文中的脚本实现也将采用该距离计算公式。对于点(x3,y3)到另外两点(x1,y1)、(x2,y2)所构成直线的距离的计算公式为

即为下图中蓝色虚线所示的距离:
3.2 脚本实现
DolphinDB 支持用户通过 defg 声明编写脚本实现自定义聚合函数,并且 rolling 等滑动窗口函数支持调用用户自定义的聚合函数进行滑动计算,因此 DolphinDB 天然支持用户自定义降采样算法进行滑动计算,以下代码为 PIP 算法的脚本实现:
defg PIP(X, Y){data = table(X as x, Y as y)rowTab = select x, y, rowNo(x) as rowNo from datan = size(X)
// k为每次滑动降采样的数据量,取值范围为 3~n(n 为滑动窗口大小) k = 5 samples = 2result = string(X[0])+"_"+string(Y[0])indexList = [0,n-1]do{distanceVec = [0.0]for (i in 0..(size(indexList)-2)){start, end = indexList[i], indexList[i+1]x1, y1 = X[start], Y[start]x2, y2 = X[end], Y[end]a = (y1-y2)/(x1-x2)b = y1-a*x1distanceVec=join(distanceVec, abs(Y[(start+1): end] - (X[(start+1): end]*a + b)))distanceVec.append!(0)}distanceMax = distanceVec.max()tmp = table(rowTab, distanceVec as distance)nextPoint = select x, y, rowNo from tmp where distance = distanceMaxresult += ","+string(nextPoint.x[0])+"_"+string(nextPoint.y[0])indexList = indexList.append!(nextPoint.rowNo[0]).sort()samples = samples+1}while(samples < k)result += ","+string(X.last())+"_"+string(Y.last())return result
}3.3 算法性能
PIP 算法的时间复杂度是 O(n2),得益于 DolphinDB 内置的向量化编程,我们可以将算法的时间复杂度降低为 O(n) ,极大地提升了算法的计算性能,在单机社区版的 DolphinDB 上将 1 千万条的时间序列数据降采样至 4 万条数据只需 1.4s,并且还可以通过多线程的方式进一步提升性能。
4. 案例演示
4.1 案例脚本
本案例将以 1000 万条的正弦波动数据为例,使用 PIP 算法进行降维并展示降维前后的可视化对比,用户可以在自己的 DolphinDB 环境上运行该案例的完整代码。
- 清理环境
login('admin', '123456')
undef(all)
clearAllCache()- 自定义 PIP 算法函数及解析函数
// PIP 算法聚合函数
defg PIP(X, Y){data = table(X as x, Y as y)rowTab = select x, y, rowNo(x) as rowNo from datan = size(X)
// k 为每次滑动降采样的数据量,取值范围为 3~n(n 为滑动窗口大小) k = 5 samples = 2result = string(X[0])+"_"+string(Y[0])indexList = [0,n-1]do{distanceVec = [0.0]for (i in 0..(size(indexList)-2)){start, end = indexList[i], indexList[i+1]x1, y1 = X[start], Y[start]x2, y2 = X[end], Y[end]a = (y1-y2)/(x1-x2)b = y1-a*x1distanceVec=join(distanceVec, abs(Y[(start+1): end] - (X[(start+1): end]*a + b)))distanceVec.append!(0)}distanceMax = distanceVec.max()tmp = table(rowTab, distanceVec as distance)nextPoint = select x, y, rowNo from tmp where distance = distanceMaxresult += ","+string(nextPoint.x[0])+"_"+string(nextPoint.y[0])indexList = indexList.append!(nextPoint.rowNo[0]).sort()samples = samples+1}while(samples < k)result += ","+string(X.last())+"_"+string(Y.last())return result
}// 降采样结果解析函数
def strToTable(result){samplesPIP = keyedTable(`x`y, 1:0, `x`y, `DOUBLE`DOUBLE)for (res in result){windows = res.split(',')for (window in windows){row = window.split('_')samplesPIP.append!(table([double(row[0])] as x, [double(row[1])] as y))}}return samplesPIP.sortBy!(`x, 1)
}- 模拟数据
// 模拟 1 千万条正弦数据,大小为 153 MB
X = (double(0..9999999)*pi/1000)
Y = sin(X)- 结合
rolling函数进行滑动计算
// 调用 rolling 函数进行滑动窗口计算,每 1000 个点滑动 1 次,降采样到 10 个点
timer{pipResult = rolling(PIP, [X, Y], 1000, 999)}// 解析降采样结果输出一张表
samplesPIP = strToTable(pipResult)4.2 结果展示
DolphinDB 内置了画图函数 plot,用户可以在库内直接调用对数据进行可视化展示,接下来将调用 plot 函数可视化对比降采样前后数据。
- 原始数据折线图:
plot(Y[0:10000], X[0:10000])

- 降采样数据折线图:
plot(samplesPIP.y[0:100], samplesPIP.x[0:100])

可见,PIP 降采样算法可以完全保留数据的趋势信息。但在实际业务场景中,需结合实际业务场景合理设置滑动窗口大小及降采样点数。

![[JavaWeb]【十一】web后端开发-SpringBootWeb案例(登录)](https://img-blog.csdnimg.cn/1f1e1a0c94f54715a7406ff264e282c9.png)