题目链接:洛谷P2339 [USACO04OPEN] Turning in Homework G
首先我们考虑如何处理到达给定时间后才能交作业这一限制。其实在生活中,我们一般只会考虑什么时候交作业截止 (除了某些卷王),这样我们只用考虑如何在最大结束时间之前交作业,而不是在所有作业都没开始交之前考虑如何转悠(前者明显比后者简单),这样我们可以先二分答案贝茜交齐所有作业的总时间,再来判断能否在这时间内从原来的终点交齐作业并最终来到原来的起点。
现在考虑如何判断是否可以在给定条件下交齐所有作业。可以知道如果有三份要交的作业 \(A, B, C\),他们距离当前点的距离 \(x_A < x_B < x_C\),由图:
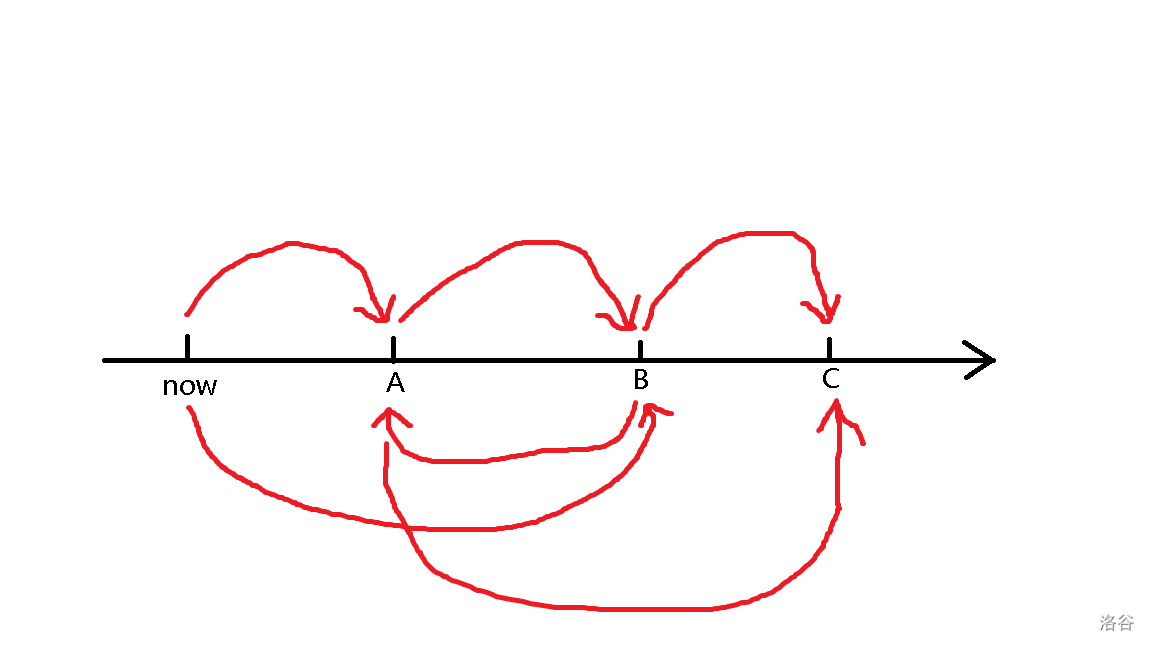
可得从起始点先到 \(A\) 再到 \(B\) 最后到 \(C\) 一定优于从 先从起点到 \(B\) 再到 \(A\) 最后到 \(C\),因此,如果贝茜要在这条走廊上来回交作业,那么她每次改变方向后所走的区间长度总小于上一次,而不是先走一个大区间,再走一个小区间,然后又走一个大区间。反过来,这就是一个从小区间推到大区间的过程,可以用区间 DP 做了。
考虑设 \(dp_{l, r, 0/1}\) 表示交完 \(l\) 到 \(r\) 区间内的作业,最后停留在左端点 \(l\) 的最小时间为 \(dp_{l, r, 0}\),停留在右端点 \(r\) 的最小时间为 \(dp_{l, r, 1}\),下面分四种情况讨论:
-
现在在某个区间的左端点,要往左继续交作业。
-
现在在某个区间的右端点,要往左继续交作业。
-
现在在某个区间的左端点,要往右继续交作业。
-
现在在某个区间的右端点,要往右继续交作业。
每种情况只用考虑到达时交作业是否截止,如果没有截止就可以更新答案,因此 DP 方程为:
注意:
-
将时间倒序后,记得将交作业截止时间更新为总时间减去原先开始交作业的时间。
-
记得将出发点与结束点也存为一个办公室,方便统计答案。
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 9;
struct Homework{int x, t;
} h[N];
bool cmp(Homework a, Homework b){if(a.x == b.x)return a.t < b.t;return a.x < b.x;
}
int C, H, B;
int tmp[N];
int dp[N][N][2];
bool chk(int tim){for(int i = 1; i <= C; i++){tmp[i] = tim - h[i].t;if(h[i].t > tim)return 0;}memset(dp, 0x3f, sizeof(dp));dp[B][B][0] = dp[B][B][1] = 0;for(int len = 2; len <= C; len++)for(int l = 1; l + len - 1 <= C; l++){int r = l + len - 1;if(dp[l + 1][r][0] + h[l + 1].x - h[l].x <= tmp[l])dp[l][r][0] = min(dp[l][r][0], dp[l + 1][r][0] + h[l + 1].x - h[l].x);if(dp[l + 1][r][1] + h[r].x - h[l].x <= tmp[l])dp[l][r][0] = min(dp[l][r][0], dp[l + 1][r][1] + h[r].x - h[l].x);if(dp[l][r - 1][1] + h[r].x - h[r - 1].x <= tmp[r])dp[l][r][1] = min(dp[l][r][1], dp[l][r - 1][1] + h[r].x - h[r - 1].x);if(dp[l][r - 1][0] + h[r].x - h[l].x <= tmp[r])dp[l][r][1] = min(dp[l][r][1], dp[l][r - 1][0] + h[r].x - h[l].x);}if(dp[1][C][0] != 0x3f3f3f3f)return 1;elsereturn 0;
}
int main(){scanf("%d%d%d", &C, &H, &B);for(int i = 1; i <= C; i++)scanf("%d%d", &h[i].x, &h[i].t);h[++C] = Homework{B, 0};++C;sort(h + 1, h + C + 1, cmp);for(int i = 1; i <= C; i++)if(h[i].x == B && h[i].t == 0){B = i;break;}int l = 1, r = N * N;while(l <= r){int mid = (l + r) >> 1;if(chk(mid))r = mid - 1;elsel = mid + 1;}printf("%d", r + 1);return 0;
}


![[39] (多校联训) A层冲刺NOIP2024模拟赛01](https://img2024.cnblogs.com/blog/3389876/202410/3389876-20241003162952457-1215604955.jpg)



![[错误代码]SQLSTATE[HY000] [1045] Access denied for user 20241001@localhost (using password: YES)](https://img2024.cnblogs.com/blog/1295962/202407/1295962-20240717124854088-281169181.jpg)
