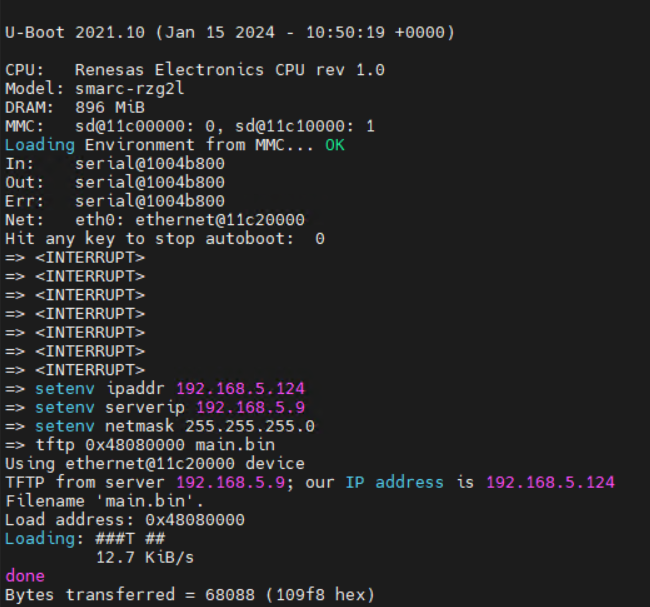
对于某些
毒瘤计数题,经常会出现统计重复或遗漏的问题,这时候就可能需要容斥一下
容斥原理
先从一个经典的例子入手:有三个学科,设为 $ S_1, S_2, S_3 $,有一堆人选不同的学科,现已知选每门学科各自有多少人选,求一共有多少人选学科;
根据题意,我们要求的就是:$ \mid S_1 \bigcup S_2 \bigcup S_3 \mid $;
考虑咋求,这是一个小学数学问题,直接用 $ |S_1| + |S_2| + |S_3| - |S_1 \bigcap S_2| - |S_2 \bigcap S_3| - |S_1 \bigcap S_3| + |S_1 \bigcap S_2 \bigcap S_3| $ 算一下即可;
其实这就是一个容斥;
扩展一下,将 $ S $ 抽象为若干个集合,对于 $ S_1, S_2, ... , S_n $,我们要求 $ | \bigcup_{i = 1}^{n} S_i | $,那么我们可以得到:
这就是容斥原理;
简记为:奇加偶减;
对于其补集同理,有:
那么,对于集合的交,我们不难得到:
其中 $ U $ 代表全集;
对于右者使用容斥原理即可;
这就是比较常用的三个公式(其实都差不多);
应用
不定方程非负整数解计数
这是本篇文章主要研究的问题;
问题: 给出不定方程 $ \sum_{i = 1}^n a_i = m $ 以及 $ n $ 个形如 $ a_i \leq b_i $ 的限制,求合法非负整数解的个数;
没有限制
我们看作有 $ n $ 个盒子,各个盒子放的球数就是对应一位 $ a $ 的值,有 $ m $ 个相同小球,盒子可以为空,求将小球放入盒子中的方案数;
如果每个盒子至少有一个球的话,那么我们可以用插板法来做,对于可以为空的情况,我们可以再加 $ n $ 个球依次放入每个盒子中,那么问题就转化成有 $ n + m $ 个小球,放入 $ n $ 个盒子中,用插板法做就是 $ \operatorname{C}_{n + m - 1}^{n - 1} $;
扩展一下,对于形如 $ \sum_{i = 1}^n a_i = m $ 以及 $ n $ 个形如 $ a_i \geq b_i $ 的限制的问题,我们可以先把对应位置放上其对应的 $ b $,那么依据上述思路答案为:
其实上述问题就是 $ \forall i \in [1, n], b_i = 0 $ 的特殊情况;
有限制
发现我们按照没有限制做会算多 $ a_i \geq b_i + 1 $ 的情况,那么我们需要容斥掉它;
考虑刚刚容斥原理中的第三个公式,答案可表示为:
其中对于 $ |\bigcup_{i = 1}^n \overline{S_i}| $,(就是 $ a_i \geq b_i + 1 $)我们应用第二个公式展开一下,得到:
随便提出一项 $ |\overline{S_i} \cap \overline{S_j} \cap \overline{S_k}| $,我们考虑它的实际意义,为 $ \sum_{i = 1}^n a_i = m $ 以及 $ 3 $ 个形如 $ a_i \geq b_i + 1 $, $ a_j \geq b_j + 1 $ $ a_k \geq b_k + 1 $ 的限制,求其方案数,依据上面的思路,可得答案为:
其他项同理;