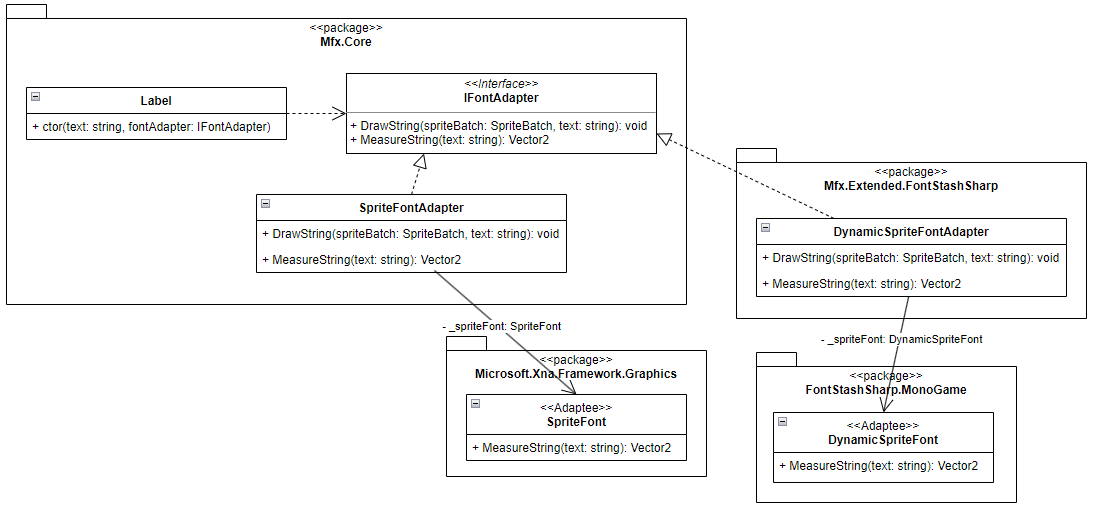
sequence
我们会发现,我们每次删的一定是长度最短的那个,所以我们可以最开始按照长的排一下序,然后用线段树维护每一个区间中还有几个数,每次加上答案后在两个端点打上标记即可
#include <bits/stdc++.h>
#define _1 (__int128)1using namespace std;
using ll = long long;void FileIO (const string s) {freopen(string(s + ".in").c_str(), "r", stdin);freopen(string(s + ".out").c_str(), "w", stdout);
}const int N = 2e5 + 10;inline int lowbit (int x) {return x & -x;
}struct Num {int l, r;
} a[N];int n, tr[N];
ll ans;void modify (int x, int lv) {while (x) tr[x] += lv, x -= lowbit(x);
}int Query (int x) {int ret = 0;while (x <= 2 * n) ret += tr[x], x += lowbit(x);return ret;
}signed main () {ios::sync_with_stdio(0), cin.tie(0);FileIO("sequence");cin >> n;for (int i = 1, x; i <= 2 * n; i++)cin >> x, a[x] = (!a[x].l ? Num{i, 0} : Num{a[x].l, i});sort(a + 1, a + n + 1, [](const Num &i, const Num &j){return i.l < j.l;});for (int i = 1; i <= n; i++)ans += a[i].r - a[i].l - Query(a[i].l) - Query(a[i].r), modify(a[i].r, 1);cout << ans;return 0;
}
slime
令 \(dp_{u, 0/1}\) 表示没有删除史莱姆操作时能得到的体积,删除一个史莱姆能减少的最大体积 。
那么我们可以显然得到两个转移
\[dp_{u, 0} = dp_{u, 0} + \sum_{v \in son_u} \max(0, dp_{v, 0} - w)\\
dp_{u, 1} = \max(dp_{u, 1}, \max_{v \in son_u}(\max(0, dp_{v, 0}) - \max(0, dp_{v,0} - dp_{v, 1} - w)))
\]
那么我们可以再设 \(ans_{u, 0/1}\) 表示将 \(u\) 作为根时不用删除可以得到史莱姆的体积,删除一个史莱姆可以减少的最大体积。
从 \(u\) 转移至 \(v\) 时,令 \(cur\) 表示 \(u\) 对 \(ans_{v, 0}\) 的贡献,\(cur = ans_{0, u} - \max(0, dp_{0, v} - w) - w\),请看图,图中解释了为什么是这个贡献
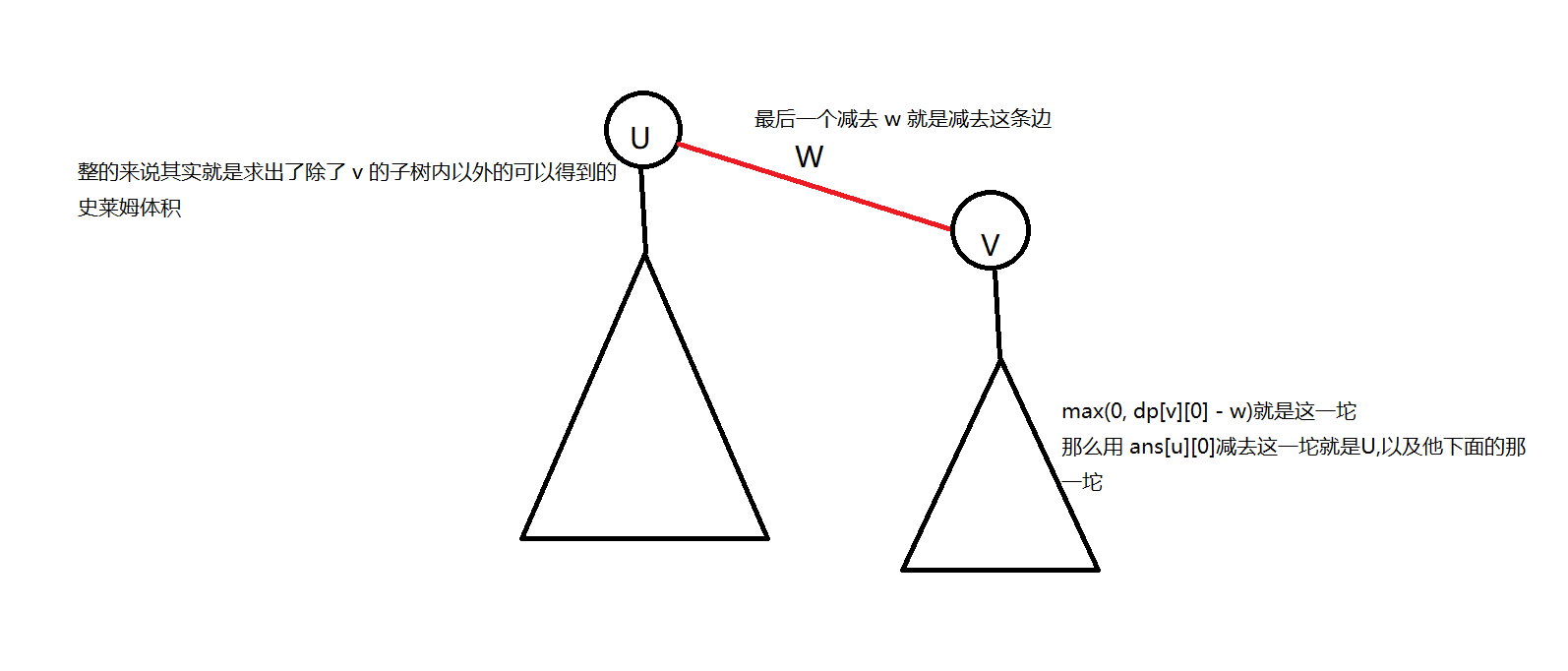
所以我们就可以轻松得出式子
\[ans_{v, 0} = dp_{v, 0} + \max(0, k)\\
ans_{v, 1} = \max(dp_{v, 1}, \max(0, k) - \max(0, k - ans_{u, 1}))
\]
查询时答案就是 \(ans_{0, c_i} - ans_{1, c_i} \times num_i\)
#include <bits/stdc++.h>using namespace std;using Pii = pair<long long, long long>;#define int long longconst int N = 2e5 + 5;int n, k, q, a[N];int dp[N][2], ans[N][2];vector<Pii> g[N];void dfs(int u, int f) {dp[u][0] = dp[u][1] = a[u];for (auto [v, w] : g[u]) {if (v == f) {continue;}dfs(v, u);int cur = dp[v][0] - w;dp[u][0] += max(0ll, cur);dp[u][1] = max(dp[u][1], max(0ll, cur) - max(0ll, cur - dp[v][1]));}
}void DFS(int u, int f) {ans[u][0] += dp[u][0];ans[u][1] = max(ans[u][1], dp[u][1]);for (auto [v, w] : g[u]) {if (v == f) {continue;}int cur = ans[u][0] - max(0ll, dp[v][0] - w) - w;ans[v][0] = max(0ll, cur);ans[v][1] = max(0ll, cur) - max(0ll, cur - ans[u][1]);DFS(v, u);}
}signed main() {ios::sync_with_stdio(0);cin.tie(0);freopen("slime.in", "r", stdin);freopen("slime.out", "w", stdout);cin >> n >> k >> q;for (int i = 1, u, v, w; i < n; i++) {cin >> u >> v >> w;g[u].push_back({v, w});g[v].push_back({u, w});}for (int i = 1, p, x; i <= k; i++) {cin >> p >> x;a[p] = x;}dfs(1, 0);DFS(1, 0);while (q--) {int u, x;cin >> u >> x;cout << ans[u][0] - x * ans[u][1] << "\n";}return 0;
}
![[42] (多校联训) A层冲刺NOIP2024模拟赛03](https://img2024.cnblogs.com/blog/3389876/202410/3389876-20241007200545323-424439879.png)