因果推断与间接效应

因果推断（Causal Inference）是统计学和数据科学中的重要分支，用于理解事件之间的因果关系，而不仅仅是相关性。与相关性分析不同，因果推断追求揭示因变量（结果）如何受到自变量（原因）的直接或间接影响。特别是，因果推断为科学研究、政策制定和商业决策提供了至关重要的工具。随着数据科学的快速发展，因果推断的应用范围也越来越广泛，从公共健康、经济学到社交网络分析，都开始深度应用该领域的理论和方法。这里将围绕因果推断的发展历程、主要理论框架以及其在直接效应和间接效应分析中的应用展开讨论，探讨因果推断如何帮助我们理解复杂的社会和自然现象。

一、因果推断的发展历程

• 早期的哲学基础
  因果关系的研究可以追溯到古希腊时期的哲学家。亚里士多德提出了“四因说”，即形式因、质料因、动力因和目的因，试图从不同角度理解事件发生的原因。近代哲学家如休谟（David Hume）则进一步提出，因果关系是我们心灵中观念的联想，并非直接从感官经验中得出，因此他认为因果关系是经验上的规律，而非必然性。这些哲学探讨为现代因果推断的理论奠定了思考的基础。

• 统计学视角的因果推断
  20世纪初，随着统计学的兴起，研究者开始尝试用数据来定量化因果关系。皮尔逊（Karl Pearson）是相关性分析的奠基者，但他坚信因果关系无法通过统计分析直接推导出。而费舍尔（Ronald A. Fisher）则通过引入随机化实验设计，提供了直接揭示因果关系的实证方法。这种方法通过随机化控制实验（RCT）避免了因果混淆因素，从而为因果推断打下了坚实的基础。

• 贝叶斯网络与结构因果模型（SCM）
  进入20世纪末，裴霖（Judea Pearl）通过贝叶斯网络和结构因果模型（Structural Causal Models，SCM）的提出，进一步推动了因果推断的现代化发展。他提出了因果推断的数学框架，利用图模型来描述变量之间的因果结构，并且通过“干预”操作来模拟现实中改变变量的方法。通过这一框架，研究者不仅可以估计变量之间的关联，还能推断在不同的干预措施下，结果变量如何变化。这一发展使得因果推断理论得到广泛应用，特别是在非实验数据的因果分析上取得了重要突破。

二、因果推断概述

2.1 因果推断的基本理论框架

• 因果图模型
  因果推断的重要工具之一是因果图模型（Causal Diagram）。通过有向无环图（DAGs），研究者可以直观地展示变量之间的因果结构。例如，节点代表变量，箭头代表因果关系。通过这种方式，可以识别出直接影响和潜在的混淆因素，从而制定更为准确的因果推断策略。
• 反事实框架
  反事实框架（Counterfactual Framework）是因果推断的核心理念之一。反事实分析要求研究者思考：“如果没有发生某个事件，会发生什么？”这一框架帮助我们理解因果关系的本质。例如，在医学研究中，研究者可能会问：“如果一个病人没有接受治疗，他们的健康状况会如何变化？”通过这种思维方式，反事实框架可以量化治疗效果或其他干预措施的因果效应。
• “干预”与“控制”
  在因果推断中，常常涉及到“干预”（Intervention）和“控制”（Control）这两个重要概念。干预意味着对某个自变量进行人为操控，控制则是为了排除混淆因素的影响。在现实中，控制的难度往往较大，因为许多因素难以直接观测或排除。结构因果模型通过图结构的分析，能够帮助识别哪些因素可以通过统计手段进行控制，从而提供合理的因果推断。

2.2 直接效应与间接效应

• 直接效应的定义
  直接效应（Direct Effect）指的是自变量对因变量的直接影响，而不通过任何中介变量。例如，在研究吸烟与肺癌之间的关系时，直接效应可以理解为吸烟对肺癌的直接因果影响，而不考虑其他潜在因素（如基因或环境）的影响。
• 间接效应的定义
  间接效应（Indirect Effect）则涉及中介变量的参与。在因果链条中，自变量首先影响中介变量，然后中介变量再影响因变量。例如，吸烟不仅直接影响肺癌的发病率，还可能通过影响呼吸系统功能这一中介因素间接作用于肺癌风险。间接效应的分析对于理解复杂系统中的多层次因果关系非常重要。
• 总效应的分解
  因果推断的一个重要任务是将总效应分解为直接效应和间接效应。总效应是指自变量对因变量的总影响，它可以通过直接效应和间接效应的累积来解释。分解总效应能够帮助我们更清楚地了解系统中的因果机制，从而为有效干预提供指导。例如，在制定公共健康政策时，了解行为（如吸烟）通过多种途径（直接和间接）影响健康的方式，可以帮助决策者设计出针对不同方面的综合干预措施。

2.3 因果推断的实际应用

• 公共健康中的应用
  因果推断在公共健康领域的应用尤为广泛，特别是在流行病学研究中。通过因果推断，研究者可以识别出潜在的疾病传播因素，并提出针对性的干预措施。例如，艾滋病、癌症、糖尿病等疾病的发病机制往往涉及多种因素的相互作用，因果推断可以帮助研究者理解不同风险因素如何通过复杂的机制共同作用，从而提出有效的防控措施。
• 社会科学中的应用
  在社会科学研究中，因果推断也被广泛应用于政策分析、社会行为研究等领域。例如，研究者可以通过因果推断方法评估某项教育政策的实施对学生成绩的影响。这类研究不仅有助于揭示政策的有效性，还能识别出政策中潜在的中介机制，从而为政策优化提供理论依据。
• 经济学中的应用
  因果推断在经济学中应用广泛，特别是在评估经济政策效果时。例如，通过分析一项税收政策对消费和投资行为的影响，经济学家可以分解出直接效应（如税收变化对企业支出的直接影响）和间接效应（如税收变化通过影响市场预期进一步影响经济活动）。这些分析为经济政策的制定和评估提供了量化的依据。
• 人工智能和机器学习中的应用
  因果推断在人工智能和机器学习中的应用近年来也受到广泛关注。传统的机器学习算法往往只关注关联关系，而忽视因果关系。然而，随着智能系统在医疗、金融等领域的应用越来越广泛，理解算法背后的因果机制变得尤为重要。例如，在自动化决策系统中，因果推断可以帮助我们设计更具鲁棒性的模型，避免因关联性误判而导致错误决策。

三、因果推断的模型

因果推断常使用线性回归模型来表征因变量 \(Y\) 与自变量 \(X\) 的关系。如果存在中介变量 \(M\)，可以通过分解总效应为直接效应和间接效应来构建因果关系。

3.1 基本模型

总效应模型

\[Y = cX + e_1 \quad \text{(总效应)} \]

其中，\(c\) 是 \(X\) 对 \(Y\) 的总效应，\(e_1\) 是误差项。

中介变量模型

如果 \(M\) 是中介变量，因果路径会经过两步，模型则变为：

\[M = aX + e_2 \quad \text{(X 对 M 的影响)} \]

\[Y = bM + c'X + e_3 \quad \text{(M 和 X 对 Y 的影响)} \]

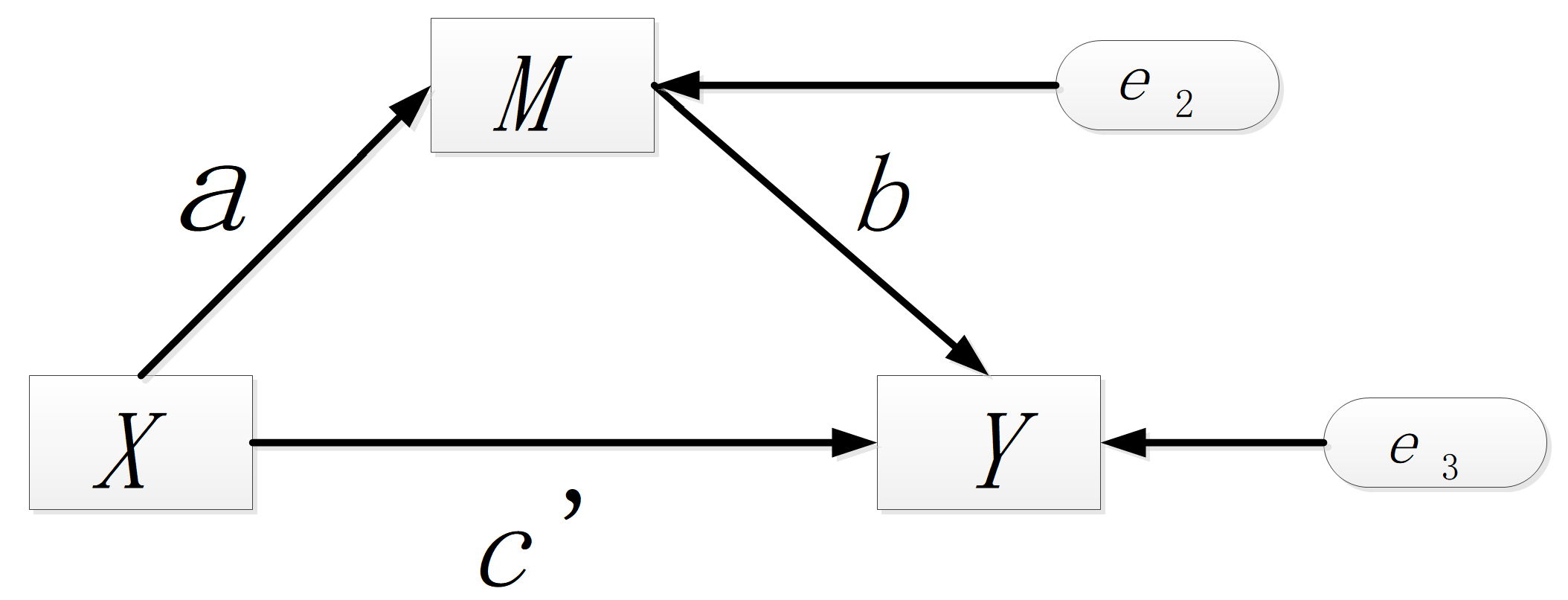
其中，\(a\) 是 \(X\) 对 \(M\) 的效应，\(b\) 是 \(M\) 对 \(Y\) 的效应，\(c'\) 是控制了 \(M\) 后 \(X\) 对 \(Y\) 的直接效应。
此时，间接效应由 \(a \times b\) 给出，总效应可分解为：

\[c = c' + ab \]

这里 \(ab\) 表示间接效应，而 \(c'\) 表示直接效应。

反事实模型

另一种常用的模型是反事实框架，该框架通过定义实际结果 \(Y_x\) 和反事实结果 \(Y_{x'}\) 来量化因果效应。干预后的因果效应表示为：

平均处理效应 (ATE)

\[\text{ATE (Average Treatment Effect)} = \mathbb{E}[Y_x - Y_{x'}] \]

ATE 衡量的是处理组和对照组之间的平均效应差。

因果效应的检验方法

逐步检验法（Baron & Kenny）
逐步检验法是经典的中介效应分析方法，主要步骤如下：

• 第一步：通过回归分析检验 \(X\) 对 \(Y\) 的总效应 \(c\) 是否显著。
• 第二步：检验 \(X\) 对中介变量 \(M\) 的效应 \(a\) 是否显著。
• 第三步：检验 \(M\) 对 \(Y\) 的效应 \(b\) 是否显著，且检验 \(X\) 在控制了 \(M\) 后对 \(Y\) 的直接效应 \(c'\) 是否显著。如果 \(a\) 和 \(b\) 显著且 \(c'\) 不显著，则存在完全中介效应；如果 \(c'\) 仍然显著，则是部分中介效应。

Sobel 检验
Sobel 检验用于直接检验间接效应是否显著，其检验统计量为：

\[z = \frac{ab}{\sqrt{b^2 \cdot s_a^2 + a^2 \cdot s_b^2}} \]

其中 \(s_a\) 和 \(s_b\) 分别是 \(a\) 和 \(b\) 的标准误。如果 \(z\) 值显著，间接效应被认为显著。

Bootstrap 法
Bootstrap 法成为检验中介效应的流行方法，因其对非正态分布数据也有较好的表现。具体步骤是从原始样本中重复抽样，并对每个样本计算间接效应 \(ab\)。通过计算间接效应的置信区间，判断间接效应是否显著。如果置信区间不包含 0，则间接效应显著。

贝叶斯方法（MCMC）
贝叶斯方法如马尔科夫链蒙特卡洛（MCMC）可用于复杂的中介效应模型检验，特别是在小样本下的情况下更具优势。通过设定先验分布并通过模拟得到后验分布来估计因果效应。

3.2 通过数据检验因果推断

• 数据准备与模型构建
  在数据检验中，首先要保证数据质量，确保自变量、因变量和中介变量的数据完整且符合模型假设。常见的数据处理步骤包括标准化、处理缺失数据等。接着根据理论假设，建立相应的模型结构。
• 回归分析
  利用回归模型估计总效应、直接效应和间接效应。通过逐步回归检验模型各项系数的显著性，可以判断中介效应的存在及其程度。
• Bootstrap 置信区间估计
  为了更准确地检验间接效应，可以使用 Bootstrap 法生成大量的模拟样本，从每个样本中计算间接效应 \(ab\)，并得到其分布。通过置信区间估计，判断间接效应是否显著。
• 假设检验
  针对直接效应和间接效应，采用 Sobel 或 Bootstrap 方法进行显著性检验。对于小样本数据，可以考虑采用贝叶斯方法进行估计，特别是在先验知识丰富的情况下。

因果推断提供了多种数学工具来量化变量间的因果关系，特别是在直接效应和间接效应的分解上具有重要应用。通过线性回归、Sobel 检验、Bootstrap 方法等多种手段，可以从数据中得出可靠的因果效应估计，并通过科学的假设检验验证其显著性。在大数据和机器学习的背景下，因果推断方法将继续在各个领域发挥关键作用。

四、案例分析

构造适合上述因果模型的数据。假设自变量 \(X\) 是教育水平（以年数为单位），因变量 \(Y\) 是年收入（以美元为单位），中介变量 \(M\) 是工作经验年数。

数据构造

假设我们有以下关系：

• 教育水平 \(X\) 会影响工作经验 \(M\)，即更多的教育可能导致更多工作经验。
• 工作经验 \(M\) 和教育水平 \(X\) 都会影响年收入 \(Y\)。

具体的数据生成模型可以如下设定：

• \(M = 2X + \epsilon_2\)，其中 \(\epsilon_2\) 是正态分布误差项，代表随机因素的影响。
• \(Y = 3M + 1.5X + \epsilon_3\)，其中 \(\epsilon_3\) 是另一个正态分布误差项，表示其他未观察到的因素的影响。

检验步骤

我们将使用逐步回归分析来验证直接效应、间接效应和总效应的显著性。此外，我们将通过 Sobel 检验和 Bootstrap 方法来进一步检验中介效应。

逐步回归分析

• 第一步：检验 \(X\) 对 \(Y\) 的总效应 \(c\) 是否显著。
• 第二步：检验 \(X\) 对中介变量 \(M\) 的效应 \(a\) 是否显著。
• 第三步：检验 \(M\) 对 \(Y\) 的效应 \(b\) 是否显著，且检验 \(X\) 在控制了 \(M\) 后对 \(Y\) 的直接效应 \(c'\) 是否显著。

Sobel 检验
Sobel 检验用于直接检验间接效应 \(a \times b\) 是否显著，其检验统计量为：

\[z = \frac{ab}{\sqrt{b^2 \cdot s_a^2 + a^2 \cdot s_b^2}} \]

其中 \(s_a\) 和 \(s_b\) 分别是 \(a\) 和 \(b\) 的标准误。如果 \(z\) 值显著，间接效应被认为显著。

Bootstrap 方法

Bootstrap 方法通过从原始样本中重复抽样，并对每个样本计算间接效应 \(a \times b\)。通过计算间接效应的置信区间，判断间接效应是否显著。如果置信区间不包含 0，则间接效应显著。通过这些步骤，我们可以验证教育水平对年收入的直接效应和通过工作经验的间接效应，从而得出教育水平如何影响年收入的结论。

import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.utils import resample
from scipy import stats# 数据生成
np.random.seed(42)
n = 500  # 样本数
X = np.random.normal(12, 2, n)  # 自变量 教育年限
e2 = np.random.normal(0, 1, n)  # 误差项 e2
M = 2 * X + e2  # 中介变量 工作经验
e3 = np.random.normal(0, 1, n)  # 误差项 e3
Y = 3 * M + 1.5 * X + e3  # 因变量 年收入# 构造 DataFrame
data = pd.DataFrame({'X': X, 'M': M, 'Y': Y})# 逐步回归分析
# 步骤1: 检验 X 对 Y 的总效应
X_with_const = sm.add_constant(X)
model1 = sm.OLS(Y, X_with_const).fit()# 步骤2: 检验 X 对 M 的效应
model2 = sm.OLS(M, X_with_const).fit()# 步骤3: 检验 X 和 M 对 Y 的效应（控制中介效应）
XM_with_const = sm.add_constant(pd.DataFrame({'X': X, 'M': M}))
model3 = sm.OLS(Y, XM_with_const).fit()# 统计结论
# 只输出 p 值的判断结果，并保留两位小数print("\n统计结论:")
# 步骤1结论
if model1.pvalues[1] < 0.05:print("1. 教育水平 X 对年收入 Y 的总效应显著，p < 0.05。")
else:print("1. 教育水平 X 对年收入 Y 的总效应不显著，p >= 0.05。")# 步骤2结论
if model2.pvalues[1] < 0.05:print("2. 教育水平 X 对工作经验 M 的影响显著，p < 0.05。")
else:print("2. 教育水平 X 对工作经验 M 的影响不显著，p >= 0.05。")# 步骤3结论
if model3.pvalues[1] < 0.05:print("3. 在控制工作经验 M 后，教育水平 X 对年收入 Y 的直接效应显著，p < 0.05。")
else:print("3. 在控制工作经验 M 后，教育水平 X 对年收入 Y 的直接效应不显著，p >= 0.05。")if model3.pvalues[2] < 0.05:print("4. 工作经验 M 对年收入 Y 的影响显著，p < 0.05。")
else:print("4. 工作经验 M 对年收入 Y 的影响不显著，p >= 0.05。")# Sobel 检验
a = model2.params[1]  # X -> M 的系数
b = model3.params[2]  # M -> Y 的系数
sa = model2.bse[1]  # X -> M 的标准误
sb = model3.bse[2]  # M -> Y 的标准误# Sobel 统计量
sobel_z = (a * b) / np.sqrt(b**2 * sa**2 + a**2 * sb**2)
sobel_p = 2 * (1 - stats.norm.cdf(np.abs(sobel_z)))print(f"\nSobel 检验: z = {sobel_z:.2f}, p = {sobel_p:.2f}")
if sobel_p < 0.05:print("5. 中介效应显著，间接效应 p < 0.05。")
else:print("5. 中介效应不显著，间接效应 p >= 0.05。")# Bootstrap 方法
def bootstrap_mediation(data, num_bootstrap=1000):boot_ab = []for _ in range(num_bootstrap):sample = resample(data)X_bs = sample['X']M_bs = sample['M']Y_bs = sample['Y']# Bootstrap 回归model_bs_1 = sm.OLS(M_bs, sm.add_constant(X_bs)).fit()model_bs_2 = sm.OLS(Y_bs, sm.add_constant(pd.DataFrame({'X': X_bs, 'M': M_bs}))).fit()a_bs = model_bs_1.params.iloc[1]  # 使用 iloc 解决 FutureWarningb_bs = model_bs_2.params.iloc[2]  # 使用 iloc 解决 FutureWarningboot_ab.append(a_bs * b_bs)boot_ab = np.array(boot_ab)return np.percentile(boot_ab, [2.5, 97.5]), np.mean(boot_ab)# 运行 Bootstrap
ci, ab_mean = bootstrap_mediation(data)
print(f"\nBootstrap 方法: ab 均值 = {ab_mean:.2f}, 95% 置信区间 = [{ci[0]:.2f}, {ci[1]:.2f}]")
if ci[0] > 0:print("6. Bootstrap 方法表明中介效应显著，95% 置信区间不包含 0。")
else:print("6. Bootstrap 方法表明中介效应不显著，95% 置信区间包含 0。")

统计结论:
1. 教育水平 X 对年收入 Y 的总效应显著，p < 0.05。
2. 教育水平 X 对工作经验 M 的影响显著，p < 0.05。
3. 在控制工作经验 M 后，教育水平 X 对年收入 Y 的直接效应显著，p < 0.05。
4. 工作经验 M 对年收入 Y 的影响显著，p < 0.05。Sobel 检验: z = 53.05, p = 0.00
5. 中介效应显著，间接效应 p < 0.05。Bootstrap 方法: ab 均值 = 6.03, 95% 置信区间 = [5.79, 6.26]
6. Bootstrap 方法表明中介效应显著，95% 置信区间不包含 0。

总结

因果推断取得了显著的进展，但在实际应用中仍然面临诸多挑战。首先，数据质量往往限制了因果推断的准确性。其次，在复杂系统中，因果关系往往具有多层次和多因多果的特性，这使得因果模型的构建和验证变得非常复杂。最后，在许多领域，干预实验的实施受到伦理和实际条件的限制，如何通过非实验数据进行可靠的因果推断仍然是一个重要的研究方向。随着大数据技术、人工智能和统计学理论的不断发展，因果推断将继续深入各个学科领域，推动更精确的科学发现和更有效的政策制定。特别是在数据日益丰富的今天，因果推断的理论与方法将在揭示复杂系统中的因果关系方面发挥越来越重要的作用。

参考资料

1. 中介因果效应分解 汇总与理解
2. 中介效应分析：方法和模型发展