day38
- 509. 斐波那契数
- 1 确定dp数组以及下标的含义
- 2 确定递推公式
- 3 dp数组如何初始化
- 4 确定遍历顺序
- 5 举例推导dp数组
- 70. 爬楼梯
- 1 确定dp数组以及下标的含义
- 2 确定递推公式
- 3 dp数组如何初始化
- 4 确定遍历顺序
- 5 举例推导dp数组
- 746. 使用最小花费爬楼梯
- 1 确定dp数组以及下标的含义
- 2 确定递推公式
- 3 dp数组如何初始化
- 4 确定遍历顺序
- 5 举例推导dp数组
509. 斐波那契数
题目链接
解题思路:动规五部曲
1 确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
2 确定递推公式
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
3 dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
dp[0] = 0;
dp[1] = 1;
4 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
5 举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
代码如下:
class Solution {
public:int fib(int N) {if( N <= 1) return N;vector<int> dp(N + 1); //定义一个N+1的数组dp[0] = 0;dp[1] = 1;for(int i = 2;i <= N;i++){dp[i] = dp[i-1] + dp[i-2];}return dp[N];}
};
70. 爬楼梯
题目链接
1 确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
2 确定递推公式
dp[i] = dp[i - 1] + dp[i - 2]
3 dp数组如何初始化
dp[1] =1;dp[2] = 2;
4 确定遍历顺序
dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
5 举例推导dp数组
当n为5的时候,dp table(dp数组)应该是这样的
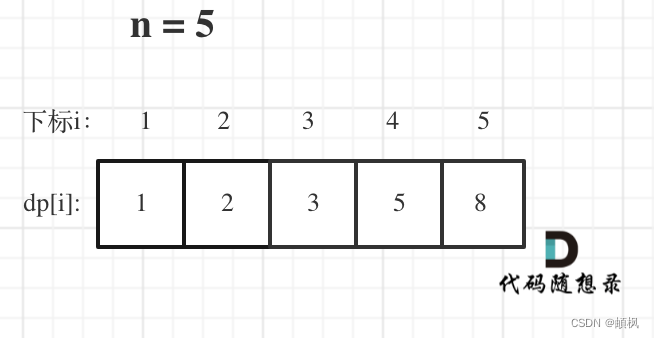
代码如下:
class Solution {
public://和斐波那契数列一样int climbStairs(int n) {if (n <= 1) return n;vector<int> dp(n + 1);dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};
746. 使用最小花费爬楼梯
题目链接
解题思路:
1 确定dp数组以及下标的含义
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]
2 确定递推公式
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
3 dp数组如何初始化
dp[0] = 0,dp[1] = 0;
4 确定遍历顺序
从前往后
5 举例推导dp数组
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
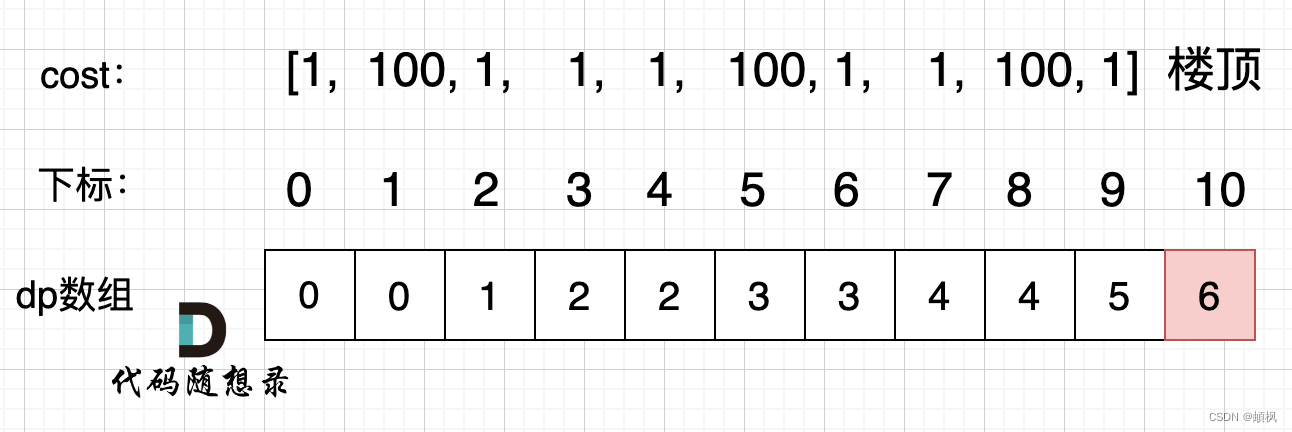
代码如下:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size() + 1);dp[0] = 0; // 默认第一步都是不花费体力的dp[1] = 0;for (int i = 2; i <= cost.size(); i++) {dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[cost.size()];}
};







![[每日一水] Latex Tikz foreach 循环嵌套](https://img-blog.csdnimg.cn/b112900e3fe74ea1b041b8ee8f1a793f.png)