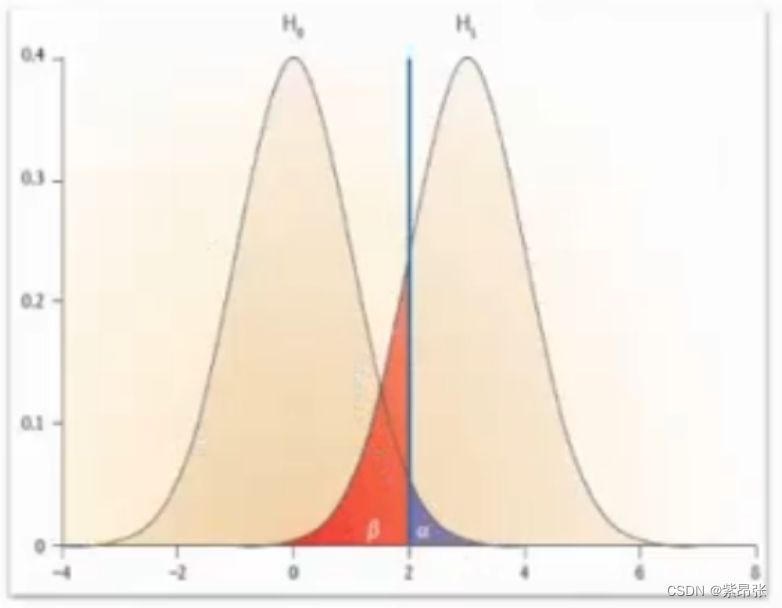
原假设 H0：一般是想要推翻的结论，如指标没有变化，实验组和对照组的该结果指标没有差异等。

备择假设 H1：一般是想要证明的结论，如实验组的指标是显著提升的，指标提升10%等。

弃真错误/一类错误/显著性水平 α：表示原假设H0为真时，但拒绝原假设的概率；通常取α=0.05或α=0.01。

置信水平 1-α：表示区间估计的可靠性。

取伪错误/二类错误 β：接受错误原假设的概率。

统计检验效力 1-β：当H0为假时，能够准确得出“拒绝H0”这个正确结论的概率，所以也称为检验效力。

概率	含义	结果
α	拒绝正确原假设的概率	×
1-α	接受正确原假设的概率	√
1-β	拒绝错误原假设的概率	√
β	接受错误原假设的概率	×

---

实例：

做了一个ABTest判断新功能上线判断效果：H0没有效果，H1有效果。

业务上的一类错误和二类错误：

一类错误：功能的改动并没有效果，但我们误认为有效果；（假设功能确实没有效果，原假设H0是成立的，但错误地认为有效果，就把功能上线了，则犯了弃真错误）。

二类错误：功能的改动有效果，但我们误认为没有效果；（假设功能有效果，则原假设H0是错误的，本应该被推翻的，但却接受了原假设，则犯了取伪错误）。

通常第一类错误更不能接受，因为宁愿砍掉几个好的策略，也不能让一个不好的策略上线。