强化学习的数学原理-03贝尔曼最优公式

目录

• 最优策略和公式推导
• 右侧最优化问题
• 公式求解以及最优性
• Contraction mapping theorem(压缩映射定理)
• 解决贝尔曼最优公式
• 分析最优策略（analyzing optimal policies）
• Summary

最优策略和公式推导

首先定义一个策略比另一个策略好：

\[v_{\pi_{1}}(s) \ge v_{\pi_{2}}(s) \quad for \quad all \quad s \in S \]

如何有上面式子成立，那么就说\(\pi_1优于\pi_2\)

基于上面的定义，于是就可以定义最优

对于所有的状态s，和所有的策略\(\pi\)都有下面的式子成立

\[v_{\pi_*}(s) \ge v_{\pi}(s) \]

那么\(\pi_*\)就是最优的(optimal)

贝尔曼最优公式：

\[\begin{align*} v(s)&=\max_{\pi}\sum_{a}\pi(a \mid s)\left( \sum_rp(r \mid s, a) + \gamma \sum_{s^{'}} p(s^{'} \mid s, a)v(s^{'}) \right), \forall s \in S \\&= \max_{\pi} \sum_a \pi(a \mid s) q(s, a), \forall s \in S \\ \end{align*}\]

对于贝尔曼最优公式实际上是一个最优化问题

我们已知的有\(p(r \mid s, a), p(s^{'} \mid s, a)\)
\(v(s),v(s^{'})\)是未知的并且需要求解的
对于贝尔曼公式\(\pi\)是已知到，对于贝尔曼最优公式\(\pi\)是未知的需要求解的。

贝尔曼最优公式的矩阵形式

\[v= \max_{\pi} (r_{\pi} + \gamma P_{\pi} v) \]

• 贝尔曼最优公式（BOE）非常elegant,它的形式非常简介，可以刻画最优的策略和最优的state value

右侧最优化问题

如何求解贝尔曼最优公式？

考虑下面的问题:

\(two \: varible \: x, a \in \mathbb{R}.\)

\[x=\max_a(2x-1-a^2). \]

上面的式子中也是含有两个未知量

先看右边的部分当\(a=0\)时达到最大值\(2x-1\)

然后将\(a=0\)带入等式右边得到\(x=2x-1\)于是就求解出了\(x=1\)

于是\(a=0,x=1\)就是这个公式的解.

下面解决贝尔曼最优方程

\[v(s)=\max_{\pi}\sum_a\pi(a \mid s) q(s,a) \]

考虑我们有3个\(q\)也就是\(q_1、q_2、q_3 \in \mathbb{R}\)找\(c_1^*、c_2^*、c_3^*\)使得\(c_1q_1+c_2q_2+c_3q_3\)最大

也就是

\[\max_{c_1、c_2、c_3}c_1q_1+c_2q_2+c_3q_3, where \: c_1+c_+c_3=1 ,and \: c_1、c_2、c_3 \ge 0 \]

为了不失一般性这里假设一个最大值,假设\(q_3 \ge q_1,q_2\)，于是最优解就是\(c_1^*=0、c_2^*=0、c_3^*=1\)

通过上面的例子就可以知道如果\(q\)值确定，如何求解上面的\(\pi\)

公式求解以及最优性

贝尔曼最优公式的矩阵形式

\[v=\max_{\pi}(r_{\pi}+\gamma P_{\pi}v) \]

我们把贝尔曼最优公式写成一个函数形式

\[f(v) := \max_{\pi}(r_{\pi} + \gamma P_{\pi} v) \]

于是最优公式就化成了

\[v=f(v) \]

\[\left[ f(v) \right]_s = max_{\pi}\sum_a\pi(a \mid s)q(s,a), s \in S \]

这里的\(f(v)\)实际上是一个向量，因为每个状态对应一个\(state \: value\)，而每一个\(state \: value \:\)都对应一个\(f(v)\)

于是问题就转化成了求解\(v=f(v)\)这个方程，求解这个方程就需要下面的知识了。

Contraction mapping theorem(压缩映射定理)

关于这个定义的详细介绍在这 | 中文数学 Wiki | Fandom

在说压缩映射定理之前需要引入一些概念

Fixed point（不动点）:

\[x \in X \: is \: a \: fixed \: point \: of \: f : \: X \rightarrow X \: if \]

\[f(x) = x \]

然后\(x\)就被称为一个不动点。

Contraction mapping or Contractive function:\(f \: is \: a \: contraction \: mapping \: if\):

\[\mid \mid f(x_1) - f(x_2) \mid \mid \le \gamma \mid \mid x_1 - x_2\mid \mid, \:where \: \gamma \in (0, 1) \]

Theorem(Contraction Mapping Thorem):

对于任何形如\(x=f(x)\)的等式，如果\(f\)是一个contraction mapping，那么有：

存在性：存在一个不动点\(x^*\)满足\(f(x^*) = x^*\)。

唯一性：不动点\(（fixed point）\)是唯一的。

求解不动点的算法：这是一个迭代式的算法,不断令\(x_{k+1}=f(x_k)\),当\(k \rightarrow \infty \:\)时\(x_k \rightarrow x^* \:\),同时收敛的速度会非常快（以指数的速度收敛）

解决贝尔曼最优公式

有了上面的压缩映射定理就可以解决贝尔曼最优公式了

\[v=f(v)=\max_{\pi}(r_{\pi + \gamma Pv}) \]

为了应用压缩映射定理，首先需要证明下式中\(\gamma \in (0,1)\)

\[\mid \mid f(v_1) - f(v_2) \mid \mid \le \gamma \mid \mid v_1 - v_2 \mid \mid \]

这个是可以得到证明的。

知道了\(f\)是一个\(contraction \: mapping\)，那么贝尔曼最优公式就可以利用上面的\(contraction \: mapping \: thorem\)解决了。

分析最优策略（analyzing optimal policies）

\[v(s) = \max_{\pi} \sum_a \pi(a \mid s) \left( \sum_r \color{red}p(r \mid s, a) r \color{black} + \color{red} \gamma \color{black} \sum_{s{'}} \color{red} p(s^{'} \mid s, a) \color{black} v(s^{'}) \color{black}\right) \]

求解贝尔曼最优公式就是已知红色量求出上面公式中黑色的量

公式中的三个量决定了optimal policy

• Reward design：\(r\)
• System model：\(p(s^{'} \mid s, a) \:, \: p(r \mid s, a)\)
• Discount rate：\(\gamma\)
• \(v(s), v(s^{'}),\pi(a \mid s)\)都是未知量待计算

1. 当\(\: \gamma \:\)比较大的时候，会比较远视，当\(\: \gamma \:\)比较小的时候则会比较短时，获得的\(\: return \:\)主要由短期的\(\: reward \:\)决定。当\(\: \gamma \:\)变为\(\: 0 \:\)时策略又会发生变化，策略会变得非常短视，更具体地说策略只会关注\(immediate \: reward\)，这样导致的结果可能是采用的策略根本到达不了\(target\)

2. 改变\(reward\)也会导致策略改变。

下面观察如果对\(\: reward \:\)进行线性变换会发生什么？\(r \rightarrow ar + b\)

• 实际上进行线性变换是不会改变最优策略的。
• 这个问题实际上并不关注\(reward\)的绝对性，更加关注\(reward\)的相对性。

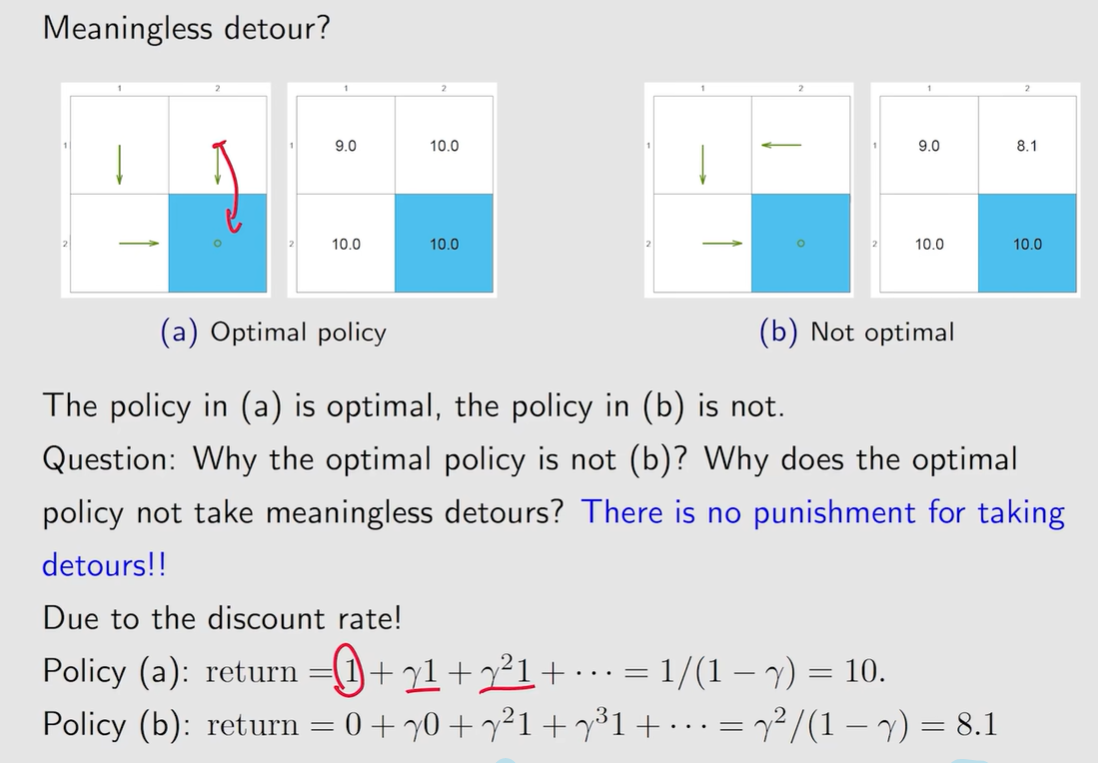
关于无意义的绕路：因为有\(\: discount \: rate \:\)的存在，会导致后面得到的\(\: reward \:\)打折扣

Summary