Codeforces Round 981 (Div. 3) 总结
A
手推一下,发现位置变化为 \(-1,2,-3,4, \dots\),所以只需要看 \(n\) 的奇偶性即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>using namespace std;
typedef long long ll;
const int N=1;
int n;
void solve()
{cin>>n;if(n&1) puts("Kosuke");else puts("Sakurako");}
int main ()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endif ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--) solve();return 0;
}B
操作时可以尽可能选择多的格子,也就是对角线尽量延伸出去,所以统计每条对角线的最小值,\((i,j)\) 所在对角线编号可以为 \(i-j\),因为有负的所以加上 \(N\)。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>using namespace std;
typedef long long ll;
const int N=505;
int n;
int a[N][N],b[N*2];
void solve()
{cin>>n;memset(b,0,sizeof b);for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) {cin>>a[i][j];b[i-j+N]=min(b[i-j+N],a[i][j]);}ll ans=0;for(int i=0;i<N*2;i++) ans-=b[i];cout<<ans<<'\n';
}
int main ()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endif ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--) solve();return 0;
}C
赛时 \(DP\) 写的(开的 vp),然后感觉比 \(E\) 还烦人 qwq。估计很多人就是这样的。设 \(f_{i,0/1}\) 为考虑前 \(i\) 个数,不交换或交换 \(i\) 与 \(n-i+1\) 的最小贡献,这样每个状态就都只与上一个有关了。那么每个位置就是有两种选择,同样上一个状态也会有两种情况,状态转移方程就好求了。
然后还需要注意初始值是最中间的位置,因此可以从最中间开始往后转移,奇偶的初始化情况有点不同。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>using namespace std;
typedef long long ll;
const int N=1e5+5;
int n;
int a[N],f[N][2];
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) f[i][0]=f[i][1]=0;if(n&1){int id=n/2+1;if(a[id]==a[id+1]) f[id+1][0]++;if(a[id]==a[id-1]) f[id+1][0]++;f[id+1][1]=f[id+1][0];for(int i=id+2;i<=n;i++) {f[i][0]=min(f[i-1][0]+(a[i]==a[i-1])+(a[n-i+1]==a[n-(i-1)+1]),f[i-1][1]+(a[i]==a[n-(i-1)+1])+(a[n-i+1]==a[i-1]));f[i][1]=min(f[i-1][0]+(a[n-i+1]==a[i-1])+(a[i]==a[n-(i-1)+1]),f[i-1][1]+(a[n-i+1]==a[n-(i-1)+1])+(a[i]==a[i-1]));}}else {int id=n/2+1;if(a[id]==a[id-1]) f[id][0]=f[id][1]=1;for(int i=id+1;i<=n;i++){f[i][0]=min(f[i-1][0]+(a[i]==a[i-1])+(a[n-i+1]==a[n-(i-1)+1]),f[i-1][1]+(a[i]==a[n-(i-1)+1])+(a[n-i+1]==a[i-1]));f[i][1]=min(f[i-1][0]+(a[n-i+1]==a[i-1])+(a[i]==a[n-(i-1)+1]),f[i-1][1]+(a[n-i+1]==a[n-(i-1)+1])+(a[i]==a[i-1]));}}cout<<min(f[n][0],f[n][1])<<'\n';
}
int main ()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endif ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--) solve();return 0;
}D
首先呢,怎么找区间是美丽的,可以用前缀和,设前缀和数组为 \(b\),当 \(b_i=b_j\) 时,说明 \([i+1,j]\) 是美丽的。那么现在已经知道了一堆美丽的区间。
抽象一下题意,其实是经典的贪心题,就是问你有一堆已知左右端点的线段,选出最多数量的线段满足其中没有线段重叠。贪心策略是:尽可能早的确定一个右边界,这样对后面的影响是最小的。所以将线段按右端点排序,先将第一条放进去,将边界确定为右端点。然后每次看下一条线段的左端点,大于边界就能取,更新边界;否则就放弃,看下一条。
然后这道题里,可以直接用 \(map\) 离散化 \(b\)。然后依次扫过去,每次出现相同的数时就是出现了一条新的线段。这样也能保证右端点小的先被考虑。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>using namespace std;
typedef long long ll;
const int N=1e5+5;
int n;
ll a[N],b[N];
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i],b[i]=b[i-1]+a[i];map<ll,ll> H;ll ans=0,ed=-1;H[0]=0;for(int i=1;i<=n;i++){if(H.count(b[i])){if(H[b[i]]>ed){ans++;ed=i;}}H[b[i]]=i+1;}cout<<ans<<'\n';
}
int main ()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endif ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--) solve();return 0;
}E
置换环问题,将 \(i\) 和 \(p_i\) 连边,那么最后肯定会出现小于等于 \(n\) 个环,例如 2 3 1 5 6 7 4 8 9:
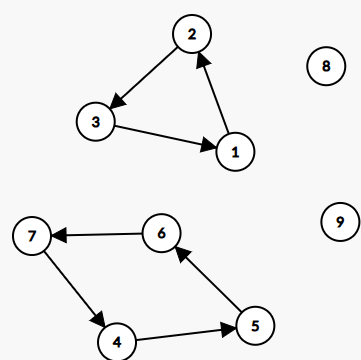
这样的话,就是要求每个环的个数小于等于 \(2\)。考虑最优交换策略。
如上图四个节点的环这个环,交换环上任一节点的左右节点,比如交换 \(6\) 左右的两个 \(p_5\) 和 \(p_7\),\(5\) 是指向 \(6\) 的,交换就能使 \(7\) 指向 \(6\),而原本 \(6\) 是指向 \(7\) 的,\(5\) 指向 \(7\) 指向的 \(4\),就将 \(6\) 和 \(7\) 独立出去了,接下来继续看环剩下的,直到大小不超过 \(2\)。
也就是说每次操作都能保证消掉两个,那么对于一个环 \(x\) 来说,需要操作的次数即为 \((size_x-1)/2\)。
用并查集统计环的大小。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>using namespace std;
typedef long long ll;
const int N=1e6+5;int n;
int a[N];
int fa[N],siz[N];
bool v[N];
int find(int x)
{if(fa[x]==x) return x;return fa[x]=find(fa[x]);
}
void merge(int x,int y)
{x=find(x),y=find(y);if(x!=y) siz[x]+=siz[y],fa[y]=x;
}
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1,v[i]=0;for(int i=1;i<=n;i++) merge(i,a[i]);int ans=0;for(int i=1;i<=n;i++){int x=find(i);if(!v[x]) ans+=(siz[x]-1)/2;v[x]=1;}cout<<ans<<'\n';
}
int main ()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endif ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--) solve();return 0;
}F
假设模数为 \(4\),模完以后得数列变为 \(1,1,2,3,1,0,1,1,2,3,1,0,1,\dots\),发现有循环节,试过几个数后大胆假设所有模数都是这样。
找到第一个为模后为 \(0\) 的位置,乘以 \(n\) 即可,严格证明我不会。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>using namespace std;
typedef long long ll;
const int N=1e6+5,mod=1e9+7;ll n,k;
ll f[N];
void solve()
{cin>>n>>k;f[1]=f[2]=1;ll id,i=3;while(1){f[i]=(f[i-1]+f[i-2])%k;if(!f[i]) {id=i;break;}i++;}if(k==1) id=1;cout<<n%mod*(id%mod)%mod<<'\n';
}
int main ()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endif ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T;cin>>T;while(T--) solve();return 0;
}