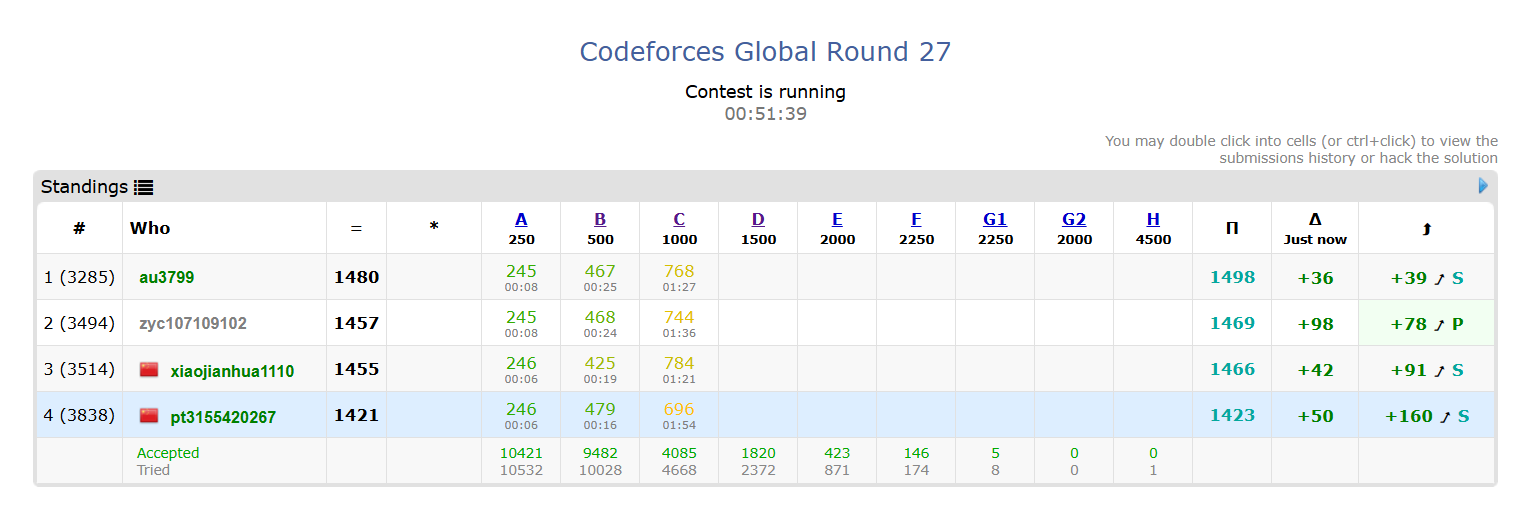
Codeforces Global Round 27 div1+2 个人题解(A~E)
Dashboard - Codeforces Global Round 27 - Codeforces
火车头
#define _CRT_SECURE_NO_WARNINGS 1#include <algorithm>
#include <array>
#include <bitset>
#include <cassert>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <chrono>
#include <fstream>
#include <functional>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <list>
#include <map>
#include <numeric>
#include <queue>
#include <random>
#include <set>
#include <stack>
#include <string>
#include <tuple>
#include <unordered_map>
#include <utility>
#include <vector>using namespace std;#define ft first
#define sd second#define yes cout << "yes\n"
#define no cout << "no\n"#define Yes cout << "Yes\n"
#define No cout << "No\n"#define YES cout << "YES\n"
#define NO cout << "NO\n"#define pb push_back
#define eb emplace_back#define all(x) x.begin(), x.end()
#define all1(x) x.begin() + 1, x.end()
#define unq_all(x) x.erase(unique(all(x)), x.end())
#define unq_all1(x) x.erase(unique(all1(x)), x.end())
#define sort_all(x) sort(all(x))
#define sort1_all(x) sort(all1(x))#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3fLL#define RED cout << "\033[91m" // 红色
#define GREEN cout << "\033[92m" // 绿色
#define YELLOW cout << "\033[93m" // 蓝色
#define BLUE cout << "\033[94m" // 品红
#define MAGENTA cout << "\033[95m" // 青色
#define CYAN cout << "\033[96m" // 青色
#define RESET cout << "\033[0m" // 重置template <typename T>
void Debug(T x, int color = 1)
{switch (color){case 1:RED;break;case 2:YELLOW;break;case 3:BLUE;break;case 4:MAGENTA;break;case 5:CYAN;break;default:break;}cout << x;RESET;
}typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
// typedef __int128_t i128;typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ld, ld> pdd;
typedef pair<ll, int> pli;
typedef pair<string, string> pss;
typedef pair<string, int> psi;
typedef pair<string, ll> psl;typedef tuple<int, int, int> ti3;
typedef tuple<ll, ll, ll> tl3;
typedef tuple<ld, ld, ld> tld3;typedef vector<bool> vb;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef vector<string> vs;
typedef vector<pii> vpii;
typedef vector<pll> vpll;
typedef vector<pli> vpli;
typedef vector<pss> vpss;
typedef vector<ti3> vti3;
typedef vector<tl3> vtl3;
typedef vector<tld3> vtld3;typedef vector<vi> vvi;
typedef vector<vl> vvl;typedef queue<int> qi;
typedef queue<ll> ql;
typedef queue<pii> qpii;
typedef queue<pll> qpll;
typedef queue<psi> qpsi;
typedef queue<psl> qpsl;typedef priority_queue<int> pqi;
typedef priority_queue<ll> pql;typedef map<int, int> mii;
typedef map<int, bool> mib;
typedef map<ll, ll> mll;
typedef map<ll, bool> mlb;
typedef map<char, int> mci;
typedef map<char, ll> mcl;
typedef map<char, bool> mcb;
typedef map<string, int> msi;
typedef map<string, ll> msl;
typedef map<int, bool> mib;typedef unordered_map<int, int> umii;
typedef unordered_map<ll, ll> uml;
typedef unordered_map<char, int> umci;
typedef unordered_map<char, ll> umcl;
typedef unordered_map<string, int> umsi;
typedef unordered_map<string, ll> umsl;std::mt19937_64 rng(std::chrono::steady_clock::now().time_since_epoch().count());template <typename T>
inline T read()
{T x = 0;int y = 1;char ch = getchar();while (ch > '9' || ch < '0'){if (ch == '-')y = -1;ch = getchar();}while (ch >= '0' && ch <= '9'){x = (x << 3) + (x << 1) + (ch ^ 48);ch = getchar();}return x * y;
}template <typename T>
inline void write(T x)
{if (x < 0){putchar('-');x = -x;}if (x >= 10){write(x / 10);}putchar(x % 10 + '0');
}/*#####################################BEGIN#####################################*/
void solve()
{
}int main()
{ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);// freopen("test.in", "r", stdin);// freopen("test.out", "w", stdout);int _ = 1;std::cin >> _;while (_--){solve();}return 0;
}/*######################################END######################################*/
// 链接:
A. Sliding
红色被驱逐。他们不是冒名顶替者。
有 \(n\) 行,每行 \(m\) 人。让 \(r\) 行和 \(c\) 列中的位置表示为 \((r,c)\)。从 \(1\) 开始按行主序对每个人进行编号,即编号为 \((r−1)⋅m+c\) 的人最初位于 \((r,c)\)。
位于 \((r,c)\) 的人决定离开。为了填补空缺,让离开的人编号为 \(i\)。每个编号为 \(j>i\) 的人将移动到编号为 \(j−1\) 的人最初所在的位置。下图说明了 \(n=2\)、\(m=3\)、\(r=1\) 和 \(c=2\) 的情况。
计算每个人移动的曼哈顿距离之和。如果一个人最初在 \((r_0,c_0)\),然后移动到 \((r_1,c_1)\),则曼哈顿距离为 \(|r_0−r_1|+|c_0−c_1|\)。
输入
第一行包含一个整数 \(t\) (\(1≤t≤10^4\)) — 测试用例的数量。
每个测试用例的唯一一行包含 \(4\) 个整数 \(n\)、\(m\)、\(r\) 和 \(c\) (\(1≤r≤n≤10^6\)、\(1≤c≤m≤10^6\)),其中 \(n\) 是行数,\(m\) 是列数,\((r,c)\) 是离开的人最初所在的位置。
输出
对于每个测试用例,输出一个整数,表示曼哈顿距离的总和。
示例
输入
4
2 3 1 2
2 2 2 1
1 1 1 1
1000000 1000000 1 1
输出
6
1
0
1999998000000
提示
对于第一个测试用例,编号为 \(2\) 的人离开,编号为 \(3\)、\(4\)、\(5\) 和 \(6\) 的人的移动距离分别为 \(1\)、\(3\)、\(1\) 和 \(1\)。所以答案是 \(1+3+1+1=6\)。
对于第二个测试用例,编号为 \(3\) 的人离开,编号为 \(4\) 的人移动。答案是 \(1\)。
解题思路
如图所示,找出个单元格的移动方式,并数一下它们的数量,黄色单元格数量为\((n-r)\times m\) ,绿色单元格数量为\(n-r\),蓝色单元格数量为\(m-c\)
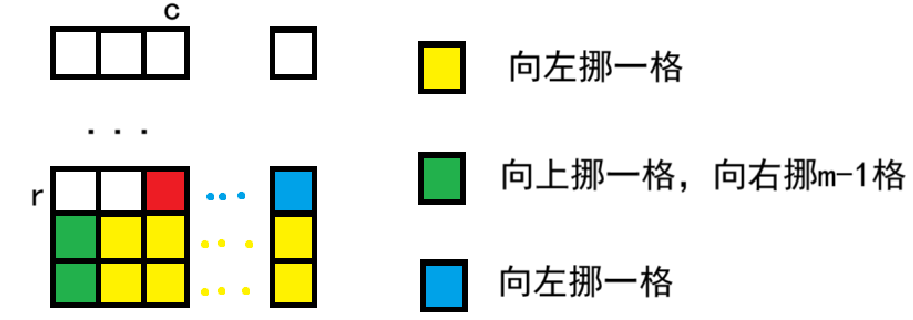
代码实现
void solve()
{ll n, m, r, c;cin >> n >> m >> r >> c;cout << (n - r) * (m - 1) + (n - r) * (m) + (m - c) << "\n";
}B. Everyone Loves Tres
有 \(3\) 个英雄和 \(3\) 个恶棍,所以总共 \(6\) 个人。
给定一个正整数 \(n\)。找到最小整数,其十进制表示长度为 \(n\),并且仅由 \(3\) 和 \(6\) 组成,并且可被 \(33\) 和 \(66\) 整除。如果不存在这样的整数,则打印 \(-1\)。
输入
第一行包含一个整数 \(t\) (\(1≤t≤500\)) — 测试用例的数量。
每个测试用例的唯一一行包含一个整数 \(n\) (\(1≤n≤500\)) — 十进制表示的长度。
输出
对于每个测试用例,如果存在所需的最小整数,则输出该整数,否则输出 \(-1\)。
示例
输入
6
1
2
3
4
5
7
输出
-1
66
-1
3366
36366
3336366
提示
对于 \(n=1\),不存在这样的整数,因为 \(3\) 和 \(6\) 都不能被 \(33\) 整除。
对于 \(n=2\),\(66\) 仅由 \(6\) 组成,并且可被 \(33\) 和 \(66\) 整除。
对于 \(n=3\),不存在这样的整数。只有 \(363\) 可被 \(33\) 整除,但不能被 \(66\) 整除。
对于 \(n=4\),\(3366\) 和 \(6666\) 都可以被 \(33\) 和 \(66\) 整除,并且 \(3366\) 最小。
解题思路
\(33\)和\(66\)的最小公倍数为\(66\),所以我们可以打个表,枚举一下\(66\)的倍数,找一下规律。
打表结果: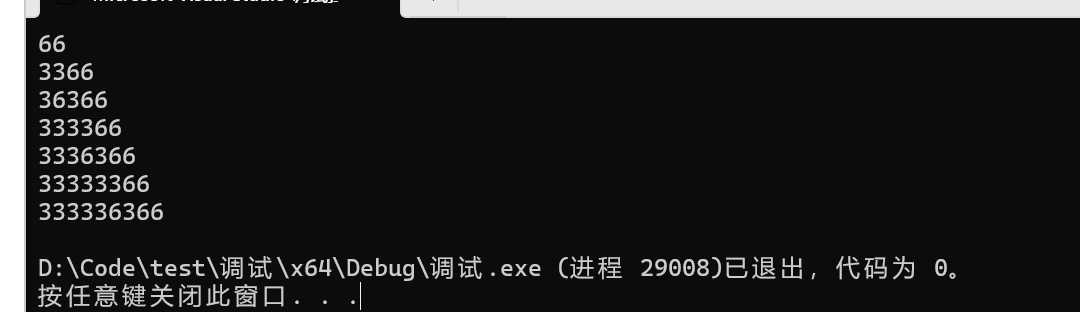
观察发现,除了1和3以外,\(n\)为偶数形式为\(3333\dots66\),奇数为\(3333\dots6366\)
代码实现
void solve()
{ll n;cin >> n;if (n == 1 || n == 3)cout << "-1\n";else{string s(n - 2, '3');s += "66";if (n & 1)s[n - 4] = '6';cout << s << endl;}
}C. Alya and Permutation
Alya 遇到了一个难题。不幸的是,她忙于竞选学生会。请帮她解决这个问题。
给定一个整数 \(n\),构造一个整数 \(1,2,…,n\) 的排列 \(p\),经过以下过程后,使 \(k\) 的值最大化(最初为 \(0\))。
对第 \(i\) 个操作(\(i=1,2,…,n\))执行 \(n\) 个操作,
如果 \(i\) 为奇数,则 \(k=k \& p_i\),其中 \(\&\) 表示按位与操作。
如果 \(i\) 为偶数,则 \(k=k | p_i\),其中 \(|\) 表示按位或运算。
输入
第一行包含一个整数 \(t\) (\(1≤t≤500\)) — 测试用例的数量。
每个测试用例的唯一一行包含一个整数 \(n\) (\(5≤n≤2 \cdot 10^5\)) — 排列的长度。
保证所有测试用例的 \(n\) 之和不超过 \(2 \cdot 10^5\)。
输出
对于每个测试用例,在第一行输出 \(k\) 的最大值,在第二行输出排列 \(p_1,p_2,…,p_n\)。
如果有多个这样的排列,则输出任意一个。
示例
输入
6
5
6
7
8
9
10
输出
5
2 1 3 4 5
7
1 2 4 6 5 3
7
2 4 5 1 3 6 7
15
2 4 5 1 3 6 7 8
9
2 4 5 6 7 1 3 8 9
15
1 2 3 4 5 6 8 10 9 7
提示
对于第一个测试用例,\(k\) 的值确定如下:
\(k=0\) 初始。
在第 \(1\) 次操作中,\(1\) 是奇数,所以 Alya 设置 \(k\) 为 \(k \& p_1=0 \& 2=0\)。
在第 \(2\) 次操作中,\(2\) 是偶数,所以 Alya 设置 \(k\) 为 \(k | p_2=0 | 1=1\)。
在第 \(3\) 次操作中,\(3\) 是奇数,所以 Alya 设置 \(k\) 为 \(k \& p_3=1 \& 3=1\)。
在第 \(4\) 次操作中,\(4\) 是偶数,所以 Alya 设置 \(k\) 为 \(k | p_4=1 | 4=5\)。
在第 \(5\) 次操作中,\(5\) 是奇数,所以 Alya 设置 \(k\) 为 \(k \& p_5=5 \& 5=5\)。
最终 \(k\) 的值为 \(5\)。可以证明,对于所有长度为 \(5\) 的排列,最终 \(k\) 的值至多为 \(5\)。另一个有效输出是 \([2,3,1,4,5]\)。
对于第二个测试用例,最终 \(k\) 的值为 \(7\)。可以证明,对于所有长度为 \(6\) 的排列,最终 \(k\) 的值至多为 \(7\)。其他有效输出包括 \([2,4,1,6,3,5]\) 和 \([5,2,6,1,3,4]\)。
解题思路
我们打个表发现,对于\(n\)为奇数,最大\(k\)值为\(n\),对于\(n\)为偶数的情况,最大\(k\)值为\(2^{len+1}-1\),其中\(len\)为\(n\)的最高二进制位。
打表结果:
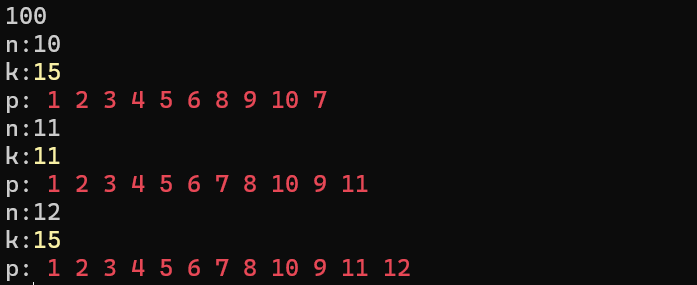
根据结果倒推最大\(k\)值如何获得
-
\(n\)为奇数
我们可以构造\(3,1,n-1,n\)这样的序列放在最末尾。
假设\(n=99\),其末尾为\(3,1,98,99\)
写成二进制形式如下:
\(0000011_2\&0000001_2 | 1100010_2 \& 1100011_2\)计算结果为\(1100011_2\),由于前一个操作是\(|\),所有无论前面是什么值,答案一定不会小于\(n\)。
-
\(n\)为偶数
我们可以构造\(3,1,2^{len}-2,2^{len}-1,n\)这样的序列放在最末尾,其中\(len\)为\(n\)的最高二进制位。
假设\(n=100\),其末尾为\(3,1,62,63,100\)
写成二进制形式如下:
\(0000011_2 \& 0000001_2 | 0111110_2 \& 0111111_2 | 1100100_2\)计算结果为\(1111111_2\),由于前一个操作是\(|\),所有无论前面是什么值,答案一定不会小于\(2^{len+1}-1\)。
注:\(n=6\)的情况要特判一下
代码实现
void solve()
{int n;cin >> n;vb vis(n + 1);if (n & 1){cout << n << "\n";vis[3] = vis[1] = vis[n - 1] = vis[n] = true;for (int i = 1; i <= n; i++){if (vis[i])continue;cout << i << " ";}cout << 3 << " " << 1 << " " << n - 1 << " " << n << "\n";}else{if (n == 6){cout << 7 << "\n";cout << "4 5 1 2 3 6\n";return;}int len = __lg(n);cout << (1 << len + 1) - 1 << "\n";int full = (1 << len) - 1;vis[3] = vis[1] = vis[full - 1] = vis[full] = vis[n] = true;for (int i = 1; i <= n; i++){if (vis[i])continue;cout << i << " ";}cout << 3 << " " << 1 << " " << full - 1 << " " << full << " " << n << "\n";}
}
D. Yet Another Real Number Problem
给定一个长度为 \(m\) 的数组 \(b\)。您可以执行以下任意次操作(可能是零次):
选择两个不同的索引 \(i\) 和 \(j\),其中 \(1 \leq i < j \leq m\) 且 \(b_i\) 为偶数,将 \(b_i\) 除以 \(2\) 并将 \(b_j\) 乘以 \(2\)。
您的任务是在执行任意数量的此类操作后最大化数组的总和。由于它可能很大,请输出此总和模数 \(10^9 + 7\)。
由于这道题太简单了,给您一个长度为 \(n\) 的数组 \(a\),您需要对 \(a\) 的每个前缀进行求解。
换句话说,表示在执行任意数量的 \(f(b)\) 这样的操作后 \(b\) 的最大和,您需要分别输出 \(f([a_1])\)、\(f([a_1,a_2])\)、…、\(f([a_1,a_2,…,a_n])\) 模数 \(10^9 + 7\)。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 10^4\)) — 测试用例的数量。
每个测试用例的第一行包含一个整数 \(n\) (\(1 \leq n \leq 2 \cdot 10^5\)) — \(a\) 的长度。
第二行包含 \(n\) 个整数 \(a_1,a_2,…,a_n\) (\(1 \leq a_i \leq 10^9\)) — 数组 \(a\) 的起始值。
保证所有测试用例的 \(n\) 之和不超过 \(2 \cdot 10^5\)。
输出
对于每个测试用例,输出 \(n\) 个整数,表示 \(a\) 模 \(10^9 + 7\) 的每个前缀的答案。
示例
输入
3
10
1 2 3 4 5 6 7 8 9 10
11
1 6 9 4 7 4 4 10 3 2 3
4
527792568 502211460 850237282 374773208
输出
1 3 8 13 46 59 126 149 1174 1311
1 7 22 26 70 74 150 1303 1306 1308 1568
527792568 83665723 399119771 773892979
注意
对于第一个示例中的每个前缀,经过操作后可能的数组是:
\([1]\) 和总和为 \(1\);
\([1,2]\) 和总和为 \(3\);
\([1,1,6]\) 和总和为 \(8\);
\([1,1,3,8]\) 和总和为 \(13\);
\([1,1,3,1,40]\) 和总和为 \(46\);
\([1,1,3,1,5,48]\) 和总和为 \(59\);
\([1,1,3,1,5,3,112]\) 和总和为 \(126\);
\([1,1,3,1,5,3,7,128]\) 和总和为 \(149\);
\([1,1,3,1,5,3,7,1,1152]\) 和总和为 \(1174\);
\([1,1,3,1,5,3,7,1,9,1280]\) 和总和为 \(1311\)。
解题思路
由于乘法的增长速度很快,所以最优的操作一定是将区间内的其它\(2\)因子尽量挪到一起。
我们可以先将\(a\)中所有元素的\(2\)因子给拆出来。
然后使用单调栈维护\([1,i-1]\)的区间最大值\(a_t\),如果\(a_t\lt a_i\),我们肯定是把\(a_t\)的所有\(2\)因子挪到\(a_i\)身上带来的贡献更多。
代码实现
const ll mod = 1e9 + 7;ll qmi(ll x, ll k, ll p = mod)
{ll res = 1;while (k){if (k & 1)res = res * x % p;x = x * x % p;k >>= 1;}return res;
}
ll cal(ll v, ll k)
{ll res = v;while (k){res <<= 1;// 防止溢出if (res > inf)return inf;k--;}return res;
}
void solve()
{int n;cin >> n;vl a(n + 1);vl cnt(n + 1);for (int i = 1; i <= n; i++){cin >> a[i];while (a[i] % 2 == 0){a[i] /= 2;cnt[i]++;}}ll sum = 0;vi stk;for (int i = 1; i <= n; i++){// 将a[i]还原后加入sumsum = (sum + a[i] * qmi(2, cnt[i]) % mod) % mod;// 单调栈维护,区间最大区间和,如果将栈顶元素小于当前a[i],直接出栈while (!stk.empty() && a[stk.back()] < cal(a[i], cnt[i])) // cal为还原函数,注意要防止溢出{int t = stk.back();// 将栈顶的2因子全部挪到a[i]上sum = (sum - a[t] * qmi(2, cnt[t]) % mod + a[t] + mod) % mod;sum = (sum - a[i] * qmi(2, cnt[i]) % mod + a[i] * qmi(2, cnt[t] + cnt[i]) % mod + mod) % mod;cnt[i] += cnt[t];stk.pop_back();}stk.eb(i);cout << sum << " \n"[i == n];}
}
E. Monster
天哪,这个原神boss太难了。幸好只用 4.99$ 就可以充值 6 个硬币。我应该小心,不要花太多钱,以免我妈妈抓到我……
你正在用一把伤害为 \(d\) 的武器与一个生命值为 \(z\) 的怪物战斗。最初, \(d=0\) 。您可以执行以下操作。
增加 \(d\) — 你的武器的伤害 \(1\) ,花费 \(x\) 个硬币。
攻击怪物,造成 \(d\) 伤害并花费 \(y\) 个硬币。
您不能连续执行第一个操作超过 \(k\) 次。
找出击败怪物所需的最少硬币数量,至少造成 \(z\) 点伤害。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 100\)) — 测试用例的数量。
每个测试用例的唯一一行包含 \(4\) 个整数 \(x\)、\(y\)、\(z\) 和 \(k\) (\(1 \leq x, y, z, k \leq 10^8\)) — 第一个操作的成本、第二个操作的成本、怪物的生命值以及第一个操作的限制。
输出
对于每个测试用例,输出击败怪物所需的最少硬币数量。
示例
输入
4
2 3 5 5
10 20 40 5
1 60 100 10
60 1 100 10
输出
12
190
280
160
提示
在第一个测试用例中,\(x=2\),\(y=3\),\(z=5\),\(k=5\)。这是一个实现最低成本 \(12\) 个硬币的策略:
- 增加伤害 \(1\),花费 \(2\) 个硬币。
- 增加伤害 \(1\),花费 \(2\) 个硬币。
- 增加伤害 \(1\),花费 \(2\) 个硬币。
- 攻击怪物,造成 \(3\) 伤害,花费 \(3\) 个硬币。
- 攻击怪物,造成 \(3\) 伤害,花费 \(3\) 个硬币。
你造成了总共 \(3+3=6\) 伤害,击败了生命值为 \(5\) 的怪物。你使用的硬币总数是 \(2+2+2+3+3=12\) 个硬币。
在第二个测试用例中,\(x=10\),\(y=20\),\(z=40\),\(k=5\)。这是一个实现最低成本 \(190\) 个硬币的策略:
- 增加伤害 \(5\),花费 \(5 \cdot x = 50\) 个硬币。
- 攻击怪物一次,造成 \(5\) 伤害,花费 \(20\) 个硬币。
- 增加伤害 \(2\),花费 \(2 \cdot x = 20\) 个硬币。
- 攻击怪物 \(5\) 次,造成 \(5 \cdot 7 = 35\) 伤害,花费 \(5 \cdot y = 100\) 个硬币。
你造成了总共 \(5+35=40\) 伤害,击败了生命值正好为 \(40\) 的怪物。你使用的硬币总数是 \(50+20+20+100=190\) 个硬币。
解题思路
暴力枚举增加伤害的最终次数,二分查找最小代价,具体实现可以看代码
代码实现
// 设置枚举次数,设置到不会超时即可,时间复杂度为Nlog(n),log(n)约为14,N可以设置成1e7
const int N = 1e7 + 5;void solve()
{ll x, y, z, k;cin >> x >> y >> z >> k;ll ans = infll;// 遍历可能的增加伤害操作的次数ifor (ll i = 0; i <= z / k + 1 && i < N; i++){ll temp = infll;// 计算剩余需要造成的伤害ll remain = z - i * (i + 1) / 2 * k - 1;// 遍历当前增加伤害后的伤害值lfor (ll l = i * k + 1; l <= i * k + k;){// 初始化rll r = i * k + k;// 计算在当前l下,剩余伤害可以被多少个l整除ll cnt = remain / l;// 如果cnt大于0,更新r为remain / cnt,确保r不超过i*k + kif (cnt > 0)r = remain / cnt;r = min(r, i * k + k);// 计算增加伤害的总成本ll sum = l * x;// 计算可以进行多少次攻击操作ll num = (l - 1) / k;// 增加攻击操作的成本sum += num * y;// 计算剩余需要造成的伤害ll re = z - num * (num + 1) / 2 * k;// 如果还有剩余的伤害,增加相应次数的攻击操作成本if (re > 0)sum += ((re - 1) / l + 1) * y;// 更新当前最小成本temp = min(temp, sum);// 移动左指针到r的下一个位置l = r + 1;}// 更新答案ans = min(ans, temp);}cout << ans << endl;
}
打表场,C题陆陆续续折腾了一个多小时,在那里打表找规律,人快麻了。
C题浪费太多时间了,D写完了但是取模有点问题没来的及调完。哎,做的最不顺心的一场。