复盘
T1。好像很好做。先想了一个 \(\mathcal O(n |c_{i,j}|^2)\) 但是带四倍常数的做法。感觉加上一些优化和卡常后问题不大。于是开写。
代码好长!!!调试好久!!!
调完后样例 6 跑 20s,最终优化后还是 7s。实在优化不了了于是考虑换做法。
发现枚举三条边后,剩下的用类似扫描线边扫边用树状数组维护即可。复杂度跟上面一样,但是没了四倍常数,而且树状数组跑的飞快。于是写。
然后又调了好久。
最后样例 6 2.7s。时限 2s 但实在优化不动了。弃之。
笑点解析:
结果就样例 6 超时。
T2。二分是肯定的。然后呢?特殊性质是什么玩意?
哦性质 C 好简单写了。\(n \le 20\) 好简单写了。然后没一点思路。
T3。出题人l了t大的。化身总司令跑路。
T4 什么牛魔题面?\(k \le [2,4]\)?哦 \(k=2\) 就是个二维数点模板题。快写。
然后没写完。
预期 \(?+45+0+0\),实际 \(100+50+4+0=154\)。T1 竟然过了。T2 算错分了,确实应该是 \(50\)。T3 过了 \(T = 1\)???
总结
- 好的:
- T1 过了。
- T2 想到了二分(虽然是最简单的一步)
- 不足:
- T4 丢了 \(17\) 分。
- T3, T4 读懂题的时间太晚啦。
知识点
- T1:枚举,二维数点。
- T2:二分,猜结论。
题解
A. 消毒
我们为每种病毒,画一个能完全包含住所有这种病毒的矩形。那么问题就变成了,选择一个面积 \(\le S\) 的矩形,使得其包含的病毒矩形数量最大。
注意到病毒矩形只有 \(500\) 种,而答案矩阵的边如果能贴着某个病毒矩形的边一定更优。也就是说答案矩形的上下左右边界分别只有 \(500\) 种可能的取值。
不妨枚举上下边界。然后把所有不在这两条线内的病毒矩形删掉。
再枚举左端点 \(l\)。此时最大的右端点 \(r\) 可以直接算出来。于是问题变成了,快速求没被删除的子矩阵中,左边界 \(\ge l\),右边界 \(\le r\) 的数量。这是一个二维数点问题,树状数组即可。
复杂度 \(\mathcal O(|c_{i,j}|^3 \log n)\)。加上一些小优化后可过。
B. 卡牌
首先二分答案。我们需要判断:是否存在一种操作方法,使得第 \(m\) 大 \(\ge mid\)。
我们将 \(\ge mid\) 的数看作 \(1\),\(< mid\) 的数看成 \(0\)。于是我们要求,有一个 \(01\) 序列,每次将奇数位置上的数写在黑板上,然后选择一个数删掉,这样操作结束后黑板上最多能有多少个 \(1\)。如果这个数量 \(\ge m\) 则 check 合法。
可以证明先将所有 \(0\) 删掉,再将剩下的 \(1\) 删掉是最优的。而所有 \(0\) 删完后剩下的 \(1\) 的贡献可以直接算(设有 \(k\) 个 \(1\),则贡献为 \(\sum_{i=1}^k\lceil \frac i2 \rceil\))。所以我们只需要考虑每一步删掉哪个 \(0\) 最优。
对于一个极长 \(1\) 段,设其长度为 \(k\)。若 \(k\) 为偶数,那么在所有 \(0\) 都删完之前的任意一轮,这其中一定会有恰好 \(\frac k2\) 个被写在黑板上(即这 \(\frac k2\) 个位置是奇数)。若 \(k\) 为奇数,我们单独拿出最左边(或最右边)的一个,那么剩下的也是一个长度为偶数的块。
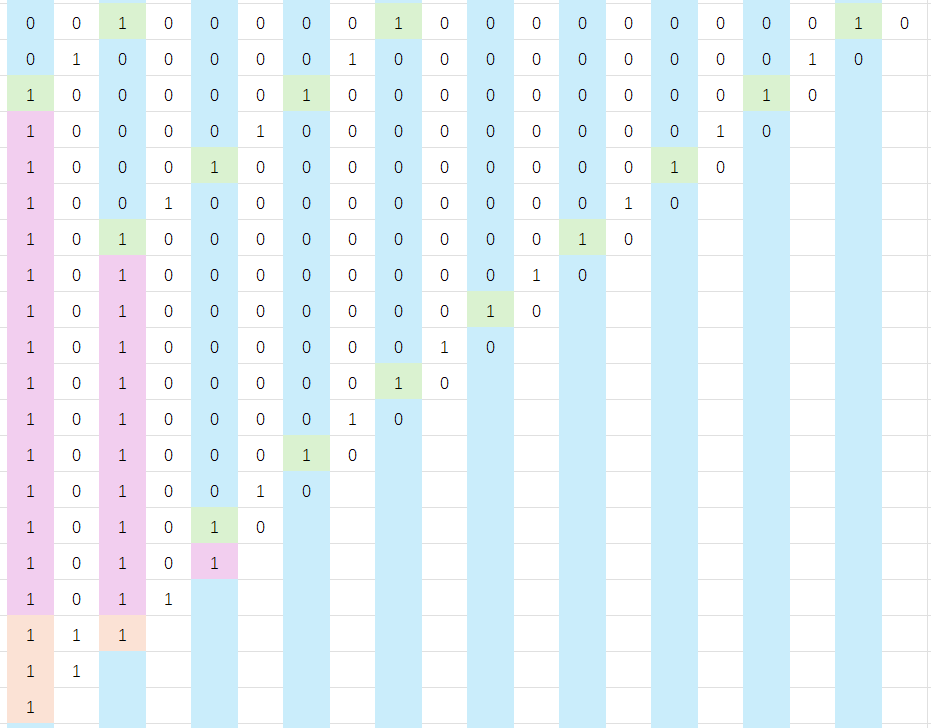
我们把上面说的偶数块的 \(1\) 的贡献提前计算好再删掉后,整个序列会变成若干个连续 \(0\) 块被 \(1\) 隔开的样子(\(0001000010101001\dots\))。考虑这样一组构造的操作方案:
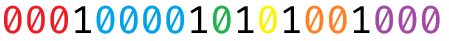
- 将 \(\color{red}000\) 全部删掉;
- 将 \(\color{blue}0000\) 的后三个删掉,变成 \(\color{blue}0\);
- \(\color{green}0\color{black},\color{yellow}0\) 不做操作;
- 将 \(\color{orange} 00\) 的最后一个删掉,变成 \(\color{orange} 0\);
- 将 \(\color{purple}000\) 全部删掉。
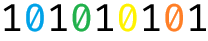
- 最后依次删掉 \(\color{purple} 0\color{black},\color{orange} 0\color{black},\color{green}0\color{black},\color{yellow}0\color{black},\color{blue}0\)。
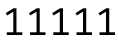
我们计算一下这样的答案。或者说,我们计算一下每个 \(1\) 在几个序列中的位置是奇数。
如何计算答案?这是最难的部分。不想说了只放张图吧(需要分别计算三种颜色的贡献):