在生活中我们会遇到各种各样的问题。有些问题非常简单;有的却非常复杂,让人们无从下手去解决。
但有些看似复杂的问题,只要我们仔细去分析它们,拨开云雾,自然就会见到“青天”。这种分析方法,就是“化繁为简”的思考模式,也就是——简化思考法。当复杂的问题被简化之后,自然就会找到解决的突破口。
例如尝试分析一下这道题目:
有A、B两个考察团,各乘一辆大客车到野外考察。每辆车上坐的都是100人。他们结伴而行。
行至途中,停车休息。两个团的人都纷纷下车,彼此相互交谈起来。停车时间虽然不长,但很多人都由生变熟,成了朋友。
休息后再上车时,有人就换了车——登上了对方的车,行了一阵,再次休息,队员们又有人换了车。大家坐定后,组织者看到各车仍是100人。
请问,此时哪辆车上外单位的人多?
这题乍看起来很乱,好像很复杂,但如果用简化法去分析,就会发现它并不复杂。
既然两次混合后,各车仍是100人。那就说明,A到B上去多少人,就会把B上同样多的人挤到A上来。无论A与B怎么混合,交换多少次,只要总保持各是100人,那么,各车所“混”进来的另一车的人,就总是相等的。
“A、B各是100人”这是问题的关键所在,抓住了它,问题就简单了。
这种简化的方法适用于对比较难把握的事物进行分析思考。当将问题简化之后,小的问题应该是最容易解决的。

简化法的分析模式
把复杂的问题分解简化,然后着重解决被分解后的小问题,这是一种很好的思维方式。
许多人不愿意将问题简化,相反,更喜欢把简单的问题复杂化,只是想显示自己的”聪明“而已。
其实,只要把所有让问题变得困难重重的因素消除,如累赘的字句、繁琐的条件、固化的经验等,这样你才能找到突破口。
在分析问题的过程当中,我们首先要有意识区分,你是在用简单的分析模式,还是复杂的分析模式。
有很多人,尤其是有一定经验和知识积累的人对简单的分析方法,一般都不感兴趣;有些人甚至认为让他们进行这种简单的分析是对其智商的侮辱。在他们看来,只有复杂的问题才能与其头脑相配,简单的问题无助于分析能力的提高。
其实他们错在没有搞清楚,问题的简单与复杂并不是分析的关键,而是在于他们大脑的分析模式是复杂的还是简单的。
对于一个分析模式简单的人而言,问题的信息内涵即使再丰富他也看不到,他的分析活动只会止于一个简单的层面上,甚至还会把简单的问题复杂化。
有许多人自恃阅历丰富知识渊博,常常看不起一些小问题或简单的问题,在他们看来,解决这些问题太容易了,简直就像让大学生计算”1+1等于几“那么可笑。
但情况真的像他们所想像的那样吗?还是因为他们的分析模式太简单,错误地理解了问题的实质?为什么儿童不理解1+1-2呢?为什么二进制的计算法则规定1+1=10呢?
如果一个大学生对问题的思维水平仍停留在小学生的层次上,那么即使让他去解决复杂的问题,他也只会以一种简单的思维模式,机械照搬复杂的教条去处理。
关于爱迪生和他的助手测量灯泡容积的故事,就很好说明了这一点。
阿普顿是普林斯顿大学数学系毕业的高才生,对和他一起工作但没有大学文凭的爱迪生有点瞧不起。
有一次,爱迪生让他测算一只梨形灯泡的容积。于是,他拿起灯泡,测出了它的直径高度,然后加以计算。但是灯泡不具有规则形状,它像球形,又不是球形;像圆柱体,又不完全是圆柱体。计算很复杂,即使是近似处理,也很烦琐。
他画了草围,在好几张白纸上写满了密密麻麻的数据和算式,也没算出来。正忙于实验的爱迪生等了很长时间,也不见阿普顿报告结果他走过来一看,便忍不住说道:“你应该换种方法算! ”
只见爱迪生略一沉思,快步取来一大杯水。轻轻地往阿普频刚才反复测算的灯泡里倒满了水,然后把水倒进量筒,几秒钟就量出了水的体积,当然也就等于算出了玻璃灯泡的容积。
这时羞红了脸的阿普顿傻呆呆地站在一旁,从此对爱迪生敬佩有加。
同样是测量灯泡容积,分析模式简单的助手,只想到套用书本上现成的公式和计算法则,烦琐地进行推算,而没有具体地分析面对的问题。而分析模式复杂的爱迪生,却能迅速地找到一个简便的方法。
这就是复杂分析模式与简单分析模式分析处理问题的不同之处。
前者能从多个角度、多个层次去分析问题(即使是简单的小问题),寻找最佳的解决办法;后者只能从一个角度、一个层次去看问题,其分析活动的复杂程度并不是取决于其分析模式,而是由问题的复杂性决定的。
如果用这样的简单分析模式去分析解决复杂问题,那就像用一台低配置电脑去处理复杂信息一样,结果只有两种:不是死机,就是把复杂信息胡乱处理,得出一个简单的结论。
如何培养简化法的分析模式
一个好的思维分析模式,应该培养出我们能从多角度、多层次看问题。
当然,使分析模式复杂化并不意味着将问题的处理烦琐化,去无事生非。恰恰相反,培养复杂的分析模式是为了使头脑有足够的“内存”,当遇到复杂问题时能简便快捷地予以有效处理。
很多著名的人士,从不轻视小问题或者简单的问题,反而认为可以由小见大,能从简单当中看到复杂的原因,才算是具备一流的敏锐头脑。
同时,我们也应该懂得把握问题的核心,聚焦问题的焦点,在运用复杂的分析模式时,也知道怎么抓住问题的根本,从而有效解决它们。
这才是简化分析法的宗旨。
那如何培养这种分析方法呢?有三种主要形式:
1,简化;
所谓简化,是指首先把问题化成仅仅保留主要观点的简单形式。然后审查在极限情况下解决问题的可能性,对所得到的信息加以分析。
其次,利用迄今为止所发现的关系来反驳所得到的结果,并且所得到的结果应当符合极限情况。最后检查所得到的结果是否满足根本的要求。
数学家欧拉解决“七桥问题”,就是运用这种简化的分析思维方法。
“七桥问题”是18世纪提出的一个数学问题。
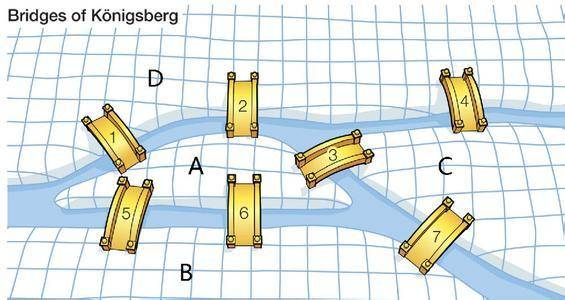
在德国哥尼斯堡,有一条布勒尔河。该河有两条支流,在城中心汇合成一条大河,河中间是岛区。河上有7座桥。
哥尼斯堡的一个大学生在傍晚散步时,总想一次走过7座桥,而每座桥只走一次。可是试来试去总是办不到。于是便写信给欧拉,请他解决这个问题。
欧拉对这个问题进行了仔细分析。他想,既然岛与半岛都是桥梁的连接地点,两岸陆地也是桥梁通往的地方,那么不妨把4处地点缩小成4个点,并把7座桥简化为7条线。
经过如此这般的抽象,欧拉就把一个有着形象因素干扰的难题转换为“一笔画问题":能否一笔画出该图而每一点只通过一次。
简言之就是,能否不重复地一笔画出该图。欧拉用已知的点、线、奇数、偶数等相关知识解决了这个问题,证明了不能由一笔画成。
这种转换虽然并没有改变问题的实质,却简化了问题,使之更加易于用数学方法予以解答。
2,分解;
在进行分析时常常需要把一些复杂的问题进行分解。
所谓分解问题,就是指把一个母问题分为几个子问题,或者把一个整体问题分为几个层次问题或局部问题,或者把一个复合系统问题分成若干个子系问题,然后分别予以解决。
如把太阳系的起源问题分解为恒星的起影问题、行星的起源问题以及卫星(如月球)的起源问题等等。
问题的分解包括目标的分解、方法(手段和途径等)的分解。
下面这个例子有助于理解这一点。
曾两度荣获世界马拉松冠军的日本选手山田本一,在谈到他取胜的秘诀时说过,在每次比赛前,他都要乘车把比赛的线路仔细看一遍,并把沿途比较醒目的标志画下来,一直画到赛程的终点。
比赛开始后,他就以百米的速度奋力地向第一个目标冲去,等达到第一个目标之后,他又以同样的速度向第二个目标冲去。
很长的赛程,就被他分解成若干个小目标轻松地跑完了。起初,他并不懂这个道理,而是把目标定在终点线上的那面旗帜,结果他跑十几千米时就疲劳不堪了。
山本田一这种分解目标的方法,实质上就是一种问题分解。虽然它比较简单,但却是用同样的思路去实施解决问题。这种做法,对于解决其他问题完全起到借鉴的作用。
对问题进行分解时,解决了各个局部问题(或子系统问题),并不等于一定是有效地解决了整体问题(或系统间题)。
比如生态问题、全球经济问题不仅要求局部地有效解决,也需要整体地有效解决。
这里主要原因在于局部问题之间有时是不协调,甚至是严重对立的。有时两个子系统问题各自的最佳解决方案不仅相互对立、相互冲突,而且会妨碍甚至危及其他子系统。
3,化归;
化归的方法同样可以运用于分析力的锻炼。
化归又称化约,它是解决复杂问题的一种方法。它要求尽量把一个复杂问题化归为以前解决的问题(或与之非常类似的问题),然后分析和说明采用哪些步骤,可以从早先的解法导致对新问题的解决。
这种方法在解决技术问题过程中经常使用。
比如在19世纪末,如果要教一名工人造汽车,那么最简单的方法也许就是教他如何改造一辆马车——去掉车辕,加上一个马达和变速器。
化归的第二层意思是指把复杂问题化归为各种要素。通过对每一个要素的内容、特点和意义进行分析,然后找出解决问题的方法和途径。
前一种化归主要是在问题的亚层次或在问题层次上寻求类比和方法移植;后一种化归则主要是在要素层次上寻求类比和借鉴方法,这种方法适用于分析基本问题和深层问题。

关于“化归”,匈牙利著名数学家P·罗莎在她的名著《无穷的玩艺》一书中曾对“化归法”作过生动的比拟。
她写道:“假设在你面前有煤气灶、水龙头、水壶和火柴,现在的任务是要烧水,你应当怎样去做?”.正确的回答是:“在水壶中放上水,点燃煤气,再把水壶放到煤气灶上。”
接着罗莎又提出第二个问题:“假设所有的条件都不变,只是水壶中已有了足够的水,这时你应该怎样去做?”对此,人们往往回答说:“点燃煤气,再把壶放到煤气灶上。”
但罗莎认为这并不是最好的回答,因为“只有物理学家才这样做,而数学家则会倒去壶中的水,并且声称我已经把后一问题化归成先前的问题了。”
这就是归化的示意案例。
掌握这种分析方法,相信你的思考能力,肯定会提升到更好的层次。