线段树 树状数组

线段树

常用于维护区间值

代码

和题解有很大差异，但是过了就好

void Pushup(int x) {s[x]=(s[x<<1]+s[x<<1|1]);
}
void Pushdown(int x,int l,int r) {s[x]=(s[x]+ad[x]*(r-l+1));if(l!=r) ad[x<<1]=(ad[x<<1]+ad[x]);if(l!=r) ad[x<<1|1]=(ad[x<<1|1]+ad[x]);ad[x]=0;
}
void Build(int x,int l,int r) {if(l==r) {s[x]=a[l];return;}int mid=(l+r)>>1;Build(x<<1,l,mid);Build(x<<1|1,mid+1,r);Pushup(x);
}
void Plus(int x,int l,int r,int k,int L,int R) {Pushdown(x,l,r);if(l>=L&&r<=R) {if(l!=r) ad[x<<1]=(ad[x<<1]+k);if(l!=r) ad[x<<1|1]=(ad[x<<1|1]+k);s[x]=(s[x]+(r-l+1)*k);return;}	int mid=(l+r)>>1;Pushdown(x<<1,l,mid);Pushdown(x<<1|1,mid+1,r);	//注意这两句if(L<=mid) Plus(x<<1,l,mid,k,L,R);if(R>mid) Plus(x<<1|1,mid+1,r,k,L,R);Pushup(x);
}
long long Quary(int x,int l,int r,int L,int R) {Pushdown(x,l,r);if(l>=L&&r<=R) return s[x];long long ans=0;int mid=(l+r)>>1;if(L<=mid) ans=(ans+Quary(x<<1,l,mid,L,R));if(R>mid) ans=(ans+Quary(x<<1|1,mid+1,r,L,R));return ans;
}

实现细节

线段树开4倍大小的原因是，一些数（如5）可能使得层数多一层

Pushup的时候俩儿子的懒标记必须传干净

Pushdown的时候注意不要让叶子节点访问子节点，不然会RE

Pushdown用法总结：

1、访问到一个节点时，啥也不干，先Pushdown消除懒标记，使得后面的分析更容易；

2、Plus函数在访问完两个儿子后，要Pushup使得x数值正确，本来两儿子Add的Pushdown可以使得懒标记消掉，但是会有儿子进不了Add，因此需要在外面Pushdown一次；

3、Pushup不会对懒标记进行操作，故Pushup前先Pushdown两个儿子保证数值正确；

代码调试

对一个区间反复加和往往能发现问题（如[1,2]，[1,1]，[2,2]，[1,3]，[2,3]……）

当然，如果能背版是最好的

区间除法

转换成减法 未解决

区间开方

link

区间gcd

区间第一个值小于k的位置

区间最大子段和

维护区间和，最大前缀和，最大后缀和，最大子段和即可

例：小白逛公园

区间限长最大子段和

区间历史版本和

题目链接

维护从开始到当前时刻的\([l,r]\)区间和的和，即求\(\displaystyle\sum_{ver=1}^mS_{ver}[l\sim r]\)

一种思路是在后一个加标记遇到前一个加标记时，下推前一个加标记统计贡献

发现这种方法意味着加标记不可合并，会退化成\(O(n^2)\)（相当于加标记只能在叶子消除）

进一步思考发现：并不是不能合并，考虑前一个标记存在时的历史和：

\(S=(s[x]+ad[x]*len_{seq})*len_{time}=s[x]*len_{time}+ad[x]*len_{time}*len_{seq}\)

这时\(ad[x]*len_{time}\)与后续时间无关（因为\(ad[x]\)被更新了），又与区间长无关，可以作为标记下传

因此另开一个标记维护即可

大数比较

对于\(10^5\)位的数的比较，可以用线段树上二分来做——在结点上挂哈希值，不同就进儿子继续比较，时间复杂度\(O(\log n)\)

例题：The Classic Problem 可持久化即可

扫描线

用于解决二维数点问题

模型：对于

线段树实现

设\(s[x]\)为\([l,r]\)的总长度，\(fac[x]\)为\([l,r]\)的实际覆盖长度,\(tag[x]\)为覆盖次数懒标记，\(tag[x]\)不为\(0\)时用\(s[x]\)更新\(fac[fa[x]]\)，否则用\(fac[x]\)

实现时发现\(tag[x]\)是难以维护的，因为\(tag[x]\)为\(0\)时不意味着儿子为\(0\)，而儿子的覆盖状态是离散的，无法获取

思考发现不同于正常线段树，\(tag[x]\)是不需要上传或下传的；当\(tag[x]=1\)时，\([l,r]\)每个点覆盖次数$ \ge 1\(，直接取\)s[x]\(即可，当\)tag[x]=0\(时，覆盖状态一定是若干个区间，而子树内的节点可以完全表示出这些区间，这些表示区间的节点\)tag[]$均 \(\ge 1\)，说明它们的\(s[]\)在前面下放\(tag[]\)时已经统计上来，存在\(fac[x]\)中了，直接取\(fac[x]\)即可

例题

P1502 窗口的星星

直接考虑矩形的价值不可行

正难则反，考虑每个点的贡献，发现每个点对一个矩形内的点有贡献，贡献转移至矩形，扫描线

李超线段树

树状数组（BIT）

参考自bestsort的博文

定义

树状数组本质上为线段树的优化，与线段树相比，它的优点在于代码简洁，时间效率高（线段树固定是\(O(logn)\)，而树状数组最坏为\(O(logn)\)），但是遇到一些非常规操作，树状数组就没有那么灵活

以下是各路收集的优质理解：

线段树的变形

在用线段树求前缀和时，发现访问的节点均为左节点，大量节点弃置不用，造成时间和空间的浪费

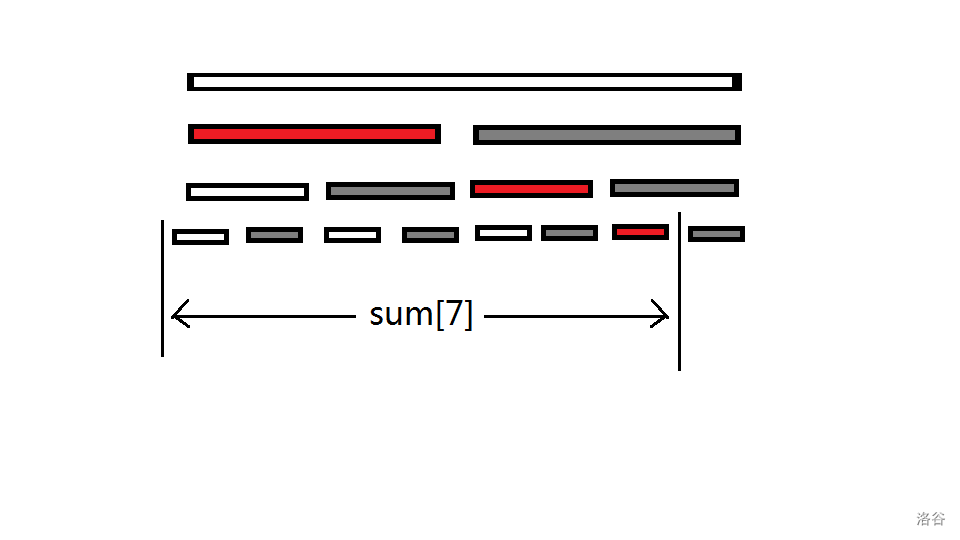
如图，灰色节点永远用不上

于是对线段树进行改进，丢掉无用点，发现剩下的节点刚好就能放进原数组里，于是原数组就被改造为树状数组

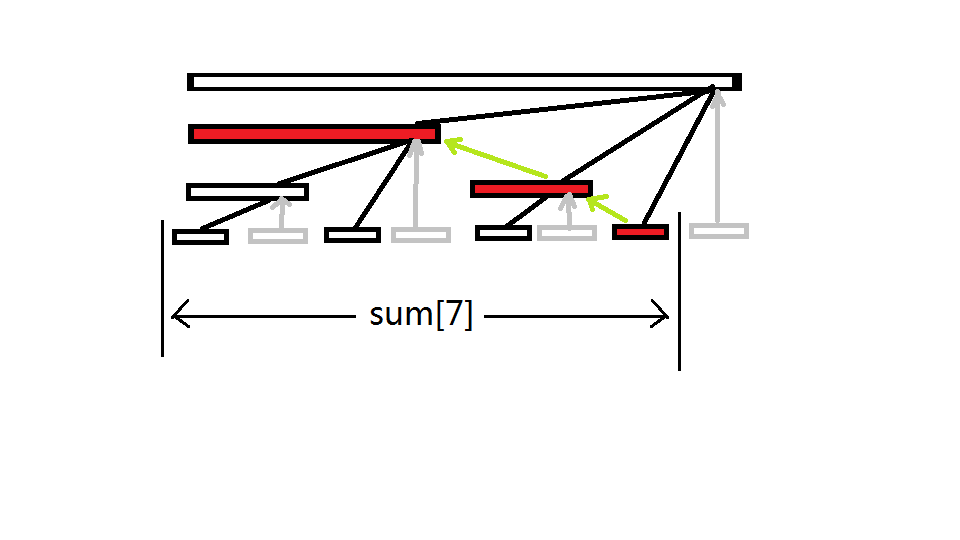
基于二进制的高效访问

空间已经优化完了，但如果还是像线段树一样从根向下一层一层跑，那就优化了个寂寞

于是有人发现了树状数组的访问规律

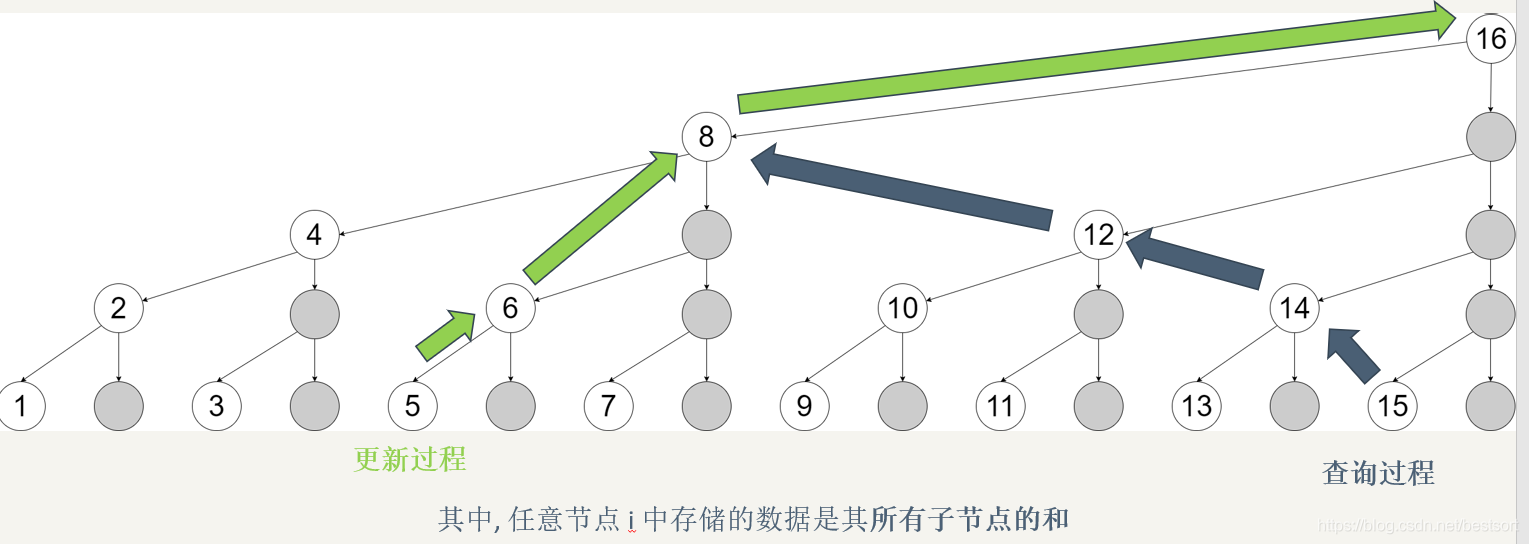
lowbit(x):取出x二进制位中最低位的1（注意取出的是1<<(i-1)不是位数i）

发现在查询时，只要不断丢掉最低位的1，就可以访问到全部前i个元素

而在单点修改时也类似，只要不断加上最低位的1，就可以完成管辖元素i的所有节点的更新

下图更清晰

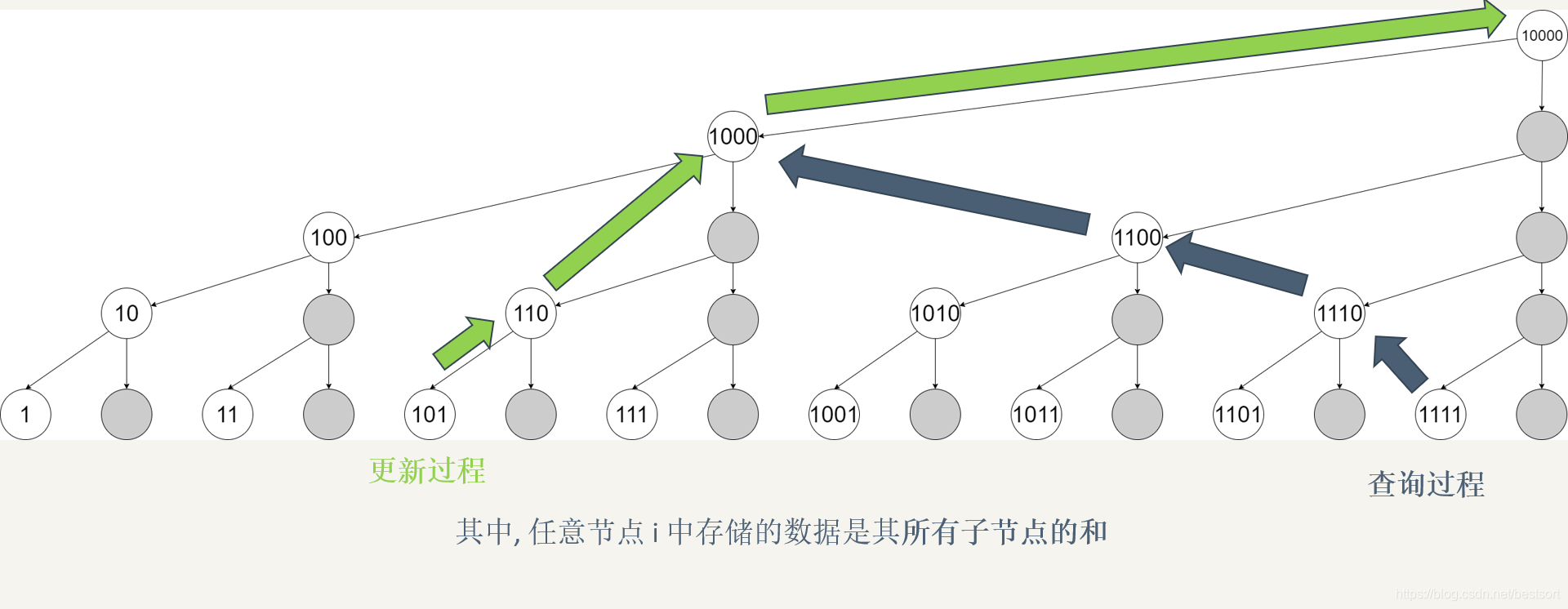
另一种理解：区间求和

观察树状数组，发现对于节点i，其实管辖的是右端点为i，长度为lowbit(i)的区间，通过i-=lowbit(i)，可以快速跳往前一个区间，达到不重不漏地访问前i个元素，易知跳转操作次数由i的二进制表示中的1的个数决定，这就是树状数组的时间复杂度最坏为\(O(logn)\)的原因

这种理解在分析二维树状数组中会很方便

单点修改，区间查询

如上文

这里求lowbit(x)用了一种基于机器编码的方法，具体证明见bestsort原文

int n,c[MAXN];	//长度为n的树状数组
int lb(int x) {return x&-x;}
void Add(int x,int k) {for(int i=x;i<=n;i+=lb(x))c[i]+=k;
}
int Quary(int x) {int ans=0;for(int i=x;i;i-=lb(x))ans+=c[i];return ans;
}Add(x,k);	//给元素x加上k
Quary(y)-Quary(x-1);	//[x,y]求和

区间修改，单点查询

考虑利用差分数组，这样前i个数的和就是元素i，而区改也能快速实现

//前面一样
Add(x,k); Add(y+1,-k);	//[x,y]加k
Quary(x);	//求元素x

区间修改，区间查询

考虑区改单查的变形

前x个元素的和为（d[]为差分数组）

\[\sum^x_{i=1}a[i]=\sum^x_{i=1}\sum^i_{j=1}d[j]=\sum^x_{i=1}(x-i+1)*d[i] \]

\[=(x+1)*\sum^x_{i=1}d[i]-\sum^x_{i=1}i*d[i] \]

记录两个数组 \(d[i]\) 和 \(s[i]=i*d[i]\) 即可

int n,d[MAXN],s[MAXN];
int lb(int x) {return x&-x;}
void Add(int x,int k) {for(int i=x;i<=n;i+=lb(x))d[i]+=k,s[i]+=k*x;
}
int Quary(int x) {int sumd=0,sums=0;for(int i=x;i;i-=lb(x))sumd+=d[i],sums+=s[i];return (x+1)*sumd-sums;
}Add(x,k); Add(y+1,-k);	//[x,y]加k
Quary(y)-Quary(x-1);	//[x,y]求和

树状数组二分

和线段树一样，树状数组也可以二分

上面提到的一种定义\(c[i]\)的方法：右端点为i，长度为lowbit(i)的区间

由于lowbit(i)为\(2^k\)，考虑类似倍增的思路

令\(pos=0\)，\(s=0\)，不断尝试对\(pos\)加上\(2^{20},2^{19},...,2^0\)，此时，\(s\)的增量为\(c[pos+2^k]\)（因为最低位是刚加上去的\(k\)），如果\(s+c[pos+2^k]<=goal\)，则加上这一位

二维树状数组

类比一维树状数组，c[x]表示右端点为x，长度为lowbit(x)的区间，则c[x][y]表示右下角坐标为(x,y)，长lowbit(x)，宽lowbit(y)的矩阵，类推转移即可

（懒得写了，现场推吧）

模型：求区间元素种类数

[P1972] HH的项链

树状数组可以快速地统计前缀和，但是遇到相同元素就会重复统计种类

由于在[l,r]中，第i种颜色只能在最后一个该颜色删除后才会消失，所以只需维护每种颜色最后出现的位置即可

01树状数组存储，st数组记录每种元素最后出现位置，若有相同元素进入，则删掉该位的1（没有贡献），更新st[]

权值线段树 & 权值树状数组

在统计个数问题上（三维偏序）有优势

求区间第k小值

权值线段树+二分即可，时间复杂度为\(O(nlogn)\)

这是主席树的底层原理之一

动态开点线段树

细节

一般开到 \(n*50\) 就差不多了

注意与动态开点线段树有关的题目，自己分析复杂度正确时TLE，有可能是炸数组了（普通线段树是RE）

线段树合并

对于一棵树，如果每个点只有\(O(1)\)的信息，要求快速求出一系列点（链或子树）的信息，可以对每个点开一棵线段树，用线段树合并维护

思路：类似于主席树，可以想到链上的该问题主席树可以维护，而到了树上，就考虑线段树合并

有两种写法，时间复杂度都是\(O(nlogn)\)

写法1：一次性

对于树\(v\to\)树$ u\(的合并，每次直接把\)v\(的结点作为\)u\(的儿子，递归处理，这样会导致\)u\(进行下一次合并时\)v\(的结构会被破坏，因此必须在\)DFS$合并后立刻访问

空间复杂度大概为\(O(n*20)\)

细节

线段树合并时，如果这么写：

	int mid=(l+r)>>1;if(!lc[now]&&lc[pre]) lc[now]=lc[pre];if(lc[now]&&lc[pre]) Merge(lc[now],lc[pre],l,mid);if(!rc[now]&&rc[pre]) rc[now]=rc[pre];if(rc[now]&&rc[pre]) Merge(rc[now],rc[pre],mid+1,r)

那么在进入第一个if后，lc[now]获得值，进入第二个if，导致出错，因此要用else分隔

写法2：可持久化

先和写法1一致，到并下一棵树时，如果有点值变化的点是\(v\)的结点，新建一个属于\(x\)的结点，把\(v\)的结点的性质拷贝过去另外做

空间复杂度大概为\(O(n*60)\)

复杂度分析

待办

应用

P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并

#3628. 「2021 集训队互测」树上的孤独

补充

对于支持线段树合并的题，都支持树链剖分（因为链和子树都在\(DFS\)序上连续），大概做法为剖询问变成\(O(logn)\)个，在\(DFS\)序数组上差分，然后扫描线/主席树

前者时间较优，后者空间较优

主席树

主席树即为可持久化线段树，思路就是对每一个历史版本都开一棵线段树，但是这样时间复杂度会很高。

由前面线段树合并可知，当点数较少时，用动态开点线段树比较优，则对于版本\(i-1\)到\(i\)的变化，如果单点变化，会有大量的节点状态不变，因此这两棵树可以共用这些节点的值，而变化的单点动态开点即可

求区间第k小值

沿用之前历史版本的思路，对每一个\([1,i]\)求一棵权值线段树，求答案时把第\(r\)棵和第\(l-1\)棵一起放进去跑线段树二分即可

可持久化数组

实际上为主席树的弱化版：对于单点修改的数组建立主席树，实际上就是只有叶子挂东西的线段树

细节

可持久化trie中叶子节点的更新是s[x]=s[pre]+1，不是s[x]++——这样写会丢失前面相同的值

P3293 [SCOI2016]美味

思考发现没有数据结构可以同时高效维护异或和加，考虑分位

我们从高位到低位考虑：要想取最大值，就要使高位尽量为\(1\)，问题转化为能否存在\([l,r]\)中的数\(a_k\)，使得当前第\(i\)位有\(bit_i(b)\oplus bit_i(a_k+x)=1\)，假设\(bit_i(b)=0\)，不难发现这样的\(a_k+x\)应在\([...\ \textcolor{red}{1}\ 00000...]\thicksim[...\ \textcolor{red}{1}\ 11111...]\)之间（\(\textcolor{red}{1}\)为第\(i\)位），找到这两个边界，记作\(l',r'\)，即为查询\([l,r]\)中有没有\([l'-x,r'-x]\)中的数，对\(a[]\)建立权值主席树即可维护

时间复杂度\(O(n\log^2n)\)，注意位运算玄学优先级

树套树

树套树实际上是一种思想——线段树的结点并不只能挂值，可以挂线段（李超树），线段树，平衡树，堆等等

一个经典问题就是二维线段树——对行开一个线段树，结点上挂统计处理\([l,r]\)这几行的信息的树

有时候第二维不一定是\(y\)坐标，也可以是时间维度，权值等

由于线段树只有\(O(\log n)\)层，在结点上开维护该区间的点的平衡树，空间复杂度为\(O(n\log n)\)（?）（动态开点线段树为\(O(n\log ^2n)\)）

基于满二叉树的数据结构

zkw线段树

非递归版线段树，具有优秀的常数

考虑将一棵线段树底层结点补成\(2^k\)个，此时，底层结点，父亲，两个儿子的下标都可以快速获取

所以这棵线段树可以从下往上跑（普通线段树都是从上往下）

区间修改

由于从下往上跑，区间标记不好下传，考虑标记永久化

在往上跑时，如果自己的兄弟也在区间内，给兄弟也打上标记

区间查询

由于标记永久化，所有的询问都得跑到根，以获取全部标记（类似李超树）

猫树

满二叉树维护无修改区间查询，预处理复杂度\(O(n\log n)\)，单次询问复杂度\(O(1)\)

先补全数组至\(2^k\)，树分为\(O(\log n)\)层，每层的结点\(i\)记录\([i,mid]\)或\([mid+1,r]\)的区间值（取决于在\(mid\)的左边还是右边）

询问时跳到\(l,r\)被\(mid\)分隔的那一层，查询这两个点的值\([l,mid],[mid+1,r]\)即可，而层数是可以快速获取的—— \(dep[LCA(l,r)]=Log_2[pos[l]]-Log_2[pos[l]\ xor\ pos[r]]\)

猫树和zkw线段树底层思想差不多，都是基于快速访问下标来优化时间，但猫树和普通线段树结构又有区别——猫树空间是\(O(n\log n)\)的，因为每一层每个位置都要维护值，而线段树空间是\(O(n)\)的