六自由度Stewart控制系统matlab仿真,带GUI界面

1.课题概述

       六自由度Stewart平台控制系统是一种高精度、高稳定性的运动模拟装置，广泛应用于飞行模拟、汽车驾驶模拟、虚拟现实、精密定位等领域。其工作原理基于Stewart机构（也称为并联机构）的设计理念，通过六个独立的线性致动器（通常为液压缸或电动推杆）连接固定基座与移动平台，实现对平台上负载在三维空间内六个自由度（三维平移X、Y、Z和三维旋转-roll、pitch、yaw）的精确控制。

 

2.系统仿真结果

 

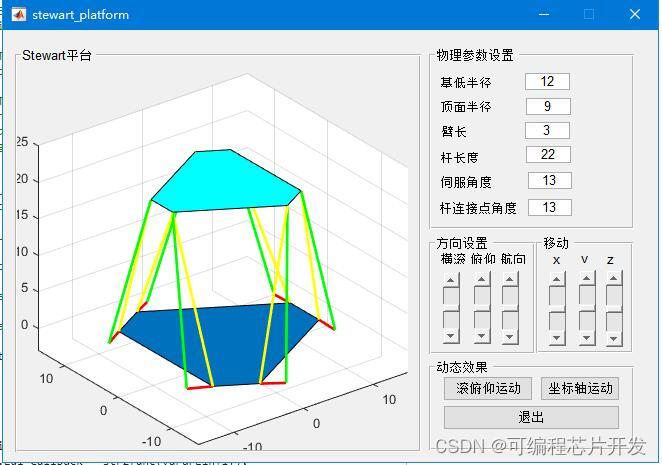
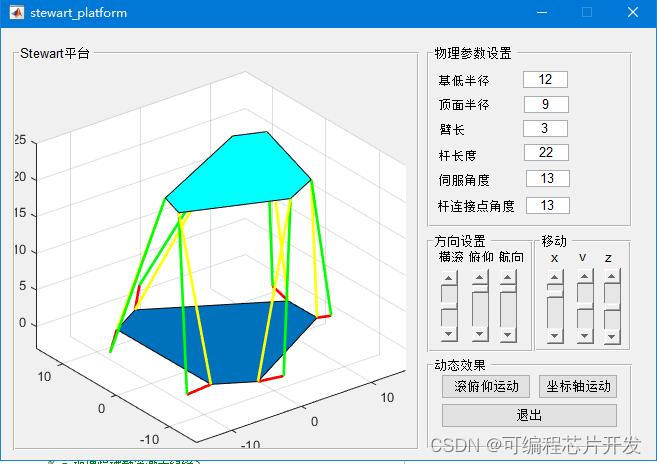
3.核心程序与模型

版本：MATLAB2022a

function x_slider_Callback(hObject, eventdata, handles)max_x= 4;       % x
min_x= -4;      % x slide= get(hObject,'Value');handles.x= slide * (max_x - min_x)  +min_x;
x_pos    = num2str(handles.x);
handles.trans(1)= handles.x;guidata(hObject, handles);stewart_cal(handles);% --- Executes during object creation, after setting all properties.
function x_slider_CreateFcn(hObject, eventdata, handles)if isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor',[.9 .9 .9]);
endmax_x= 4;       % x ?
min_x= -4;      % x ?slide= get(hObject,'Value');
handles.x= slide * (max_x - min_x)  +min_x;
handles.trans(1)= handles.x;
guidata(hObject, handles)function y_slider_Callback(hObject, eventdata, handles)max_y = 4;           % y ?
min_y = -4;          % y ?
slide= get(hObject,'Value');handles.y= slide * (max_y - min_y)  + min_y;
y_pos= num2str(handles.y);
handles.trans(2)= handles.y;guidata(hObject, handles); 
stewart_cal(handles);function y_slider_CreateFcn(hObject, eventdata, handles)if isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor',[.9 .9 .9]);
endmax_y = 4;           % y 
min_y = -4;          % y slide= get(hObject,'Value');
handles.y= slide * (max_y - min_y)  + min_y;
handles.trans(2)= handles.y;
guidata(hObject, handles); function z_slider_Callback(hObject, eventdata, handles)max_z = 4;           % z
min_z = -4;          % zslide= get(hObject,'Value');handles.z= slide * (max_z - min_z)  + min_z;
z_pos= num2str(handles.z);
handles.trans(3)= handles.z;% guidata(hObject, handles);stewart_cal(handles);
44

　　

 

4.系统原理简介

        Stewart平台由固定基座、移动平台、六个线性致动器（记为A、B、C、D、E、F）以及相应的球铰链组成。每个致动器由两段连杆构成，一段固定在基座上，另一段通过球铰链与移动平台相连。致动器内部安装有位移传感器和伺服驱动装置，可以精确控制连杆长度。致动器与平台连接点形成一个顶点，六个顶点共同定义了移动平台的几何中心。设平台几何中心为O，六个顶点分别为P_i(i=1,2,3,4,5,6)，对应致动器长度为l_i。则Stewart平台的几何构造可描述如下：

 

 

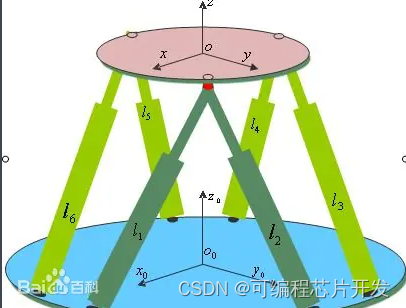
       平台运动学建模的核心是建立平台位姿（位置和姿态）与六个致动器长度之间的关系。这里采用齐次坐标系表示平台位姿，设平台当前位姿为T=[R|t]，其中R为旋转矩阵，t为平移向量。对于任意一个顶点P_i，其在基座坐标系和平台坐标系下的位置分别为P_{ib}和P_{ip}。