论文地址:https://arxiv.org/pdf/1706.03762
代码地址:https://github.com/huggingface/transformers

目录
- Introduction
- Background
- Model Architecture
- Encoder
- LN and BN
- Decoder
- Attention
- Multi-head Attention
- Feed-Forward
- Postion Encoding
- Encoder
Introduction
- RNN,LSTM 处理时序信息的局限性:无法并行,部分历史信息会在后面丢弃
- 编码器与解码器结构
- proposed transformer:纯注意力机制
Background
- CNN 替换 RNN:无法对时序信息进行建模——自注意力可以解决;CNN 可以多个输出通道——多头注意力机制
- Memory-Network
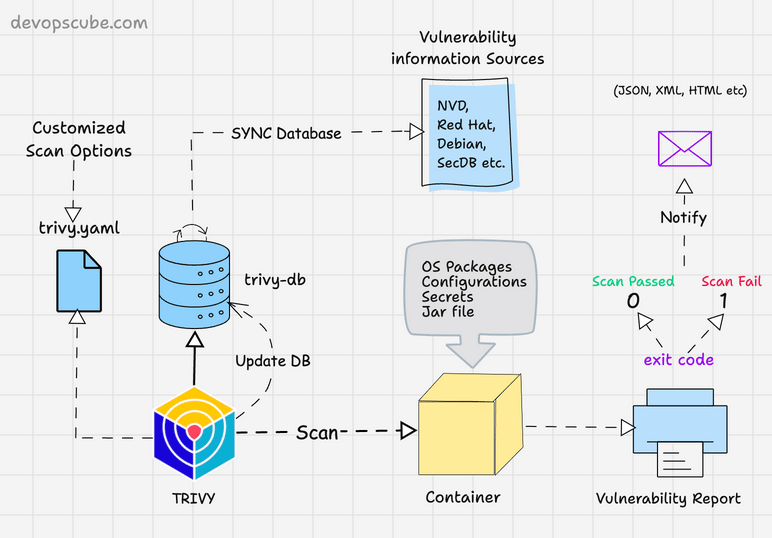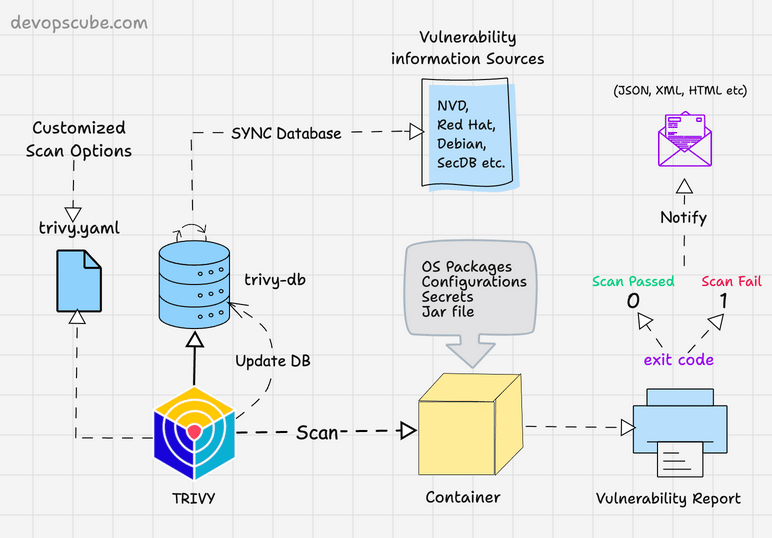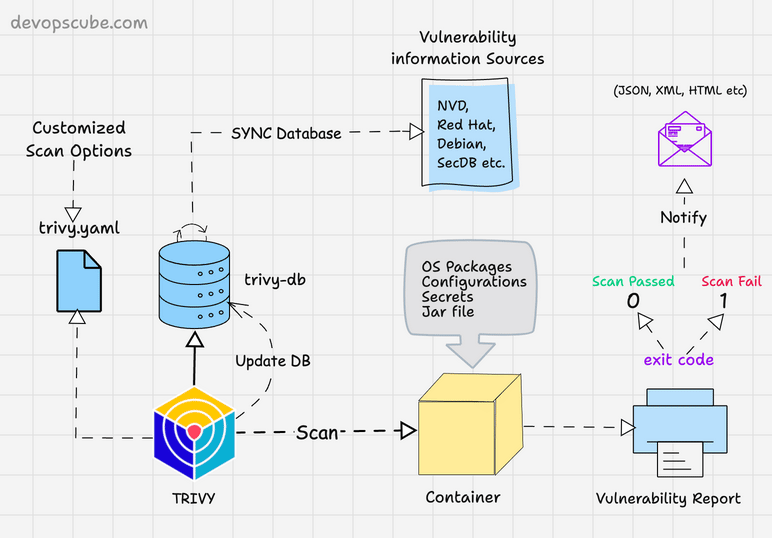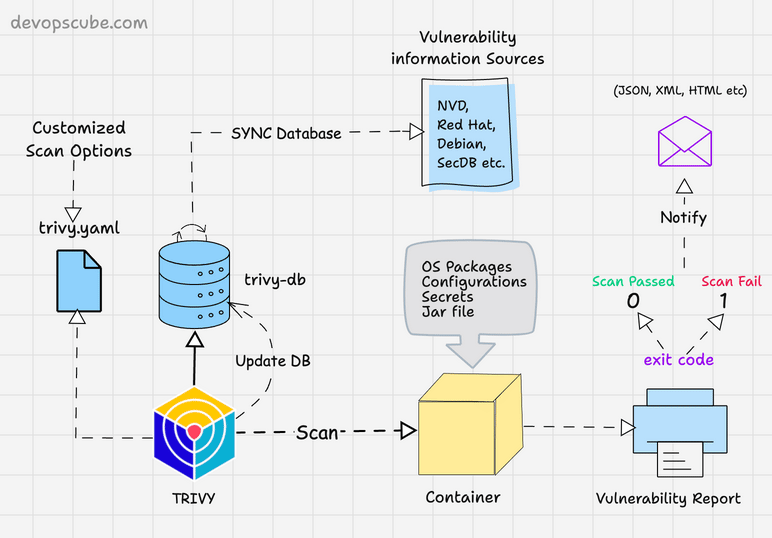
Model Architecture
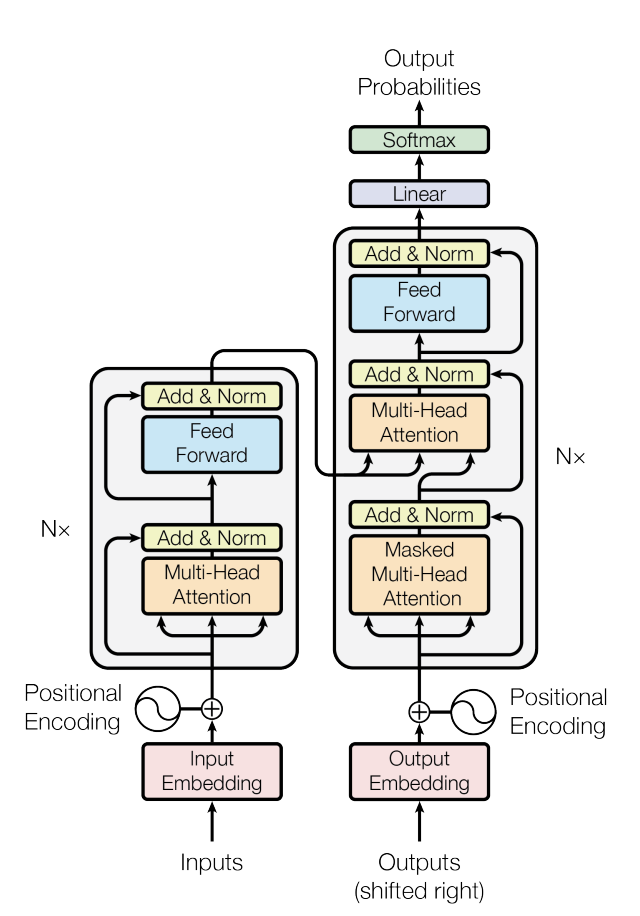
图 1:Transformer 架构
- Encoder:$\text{input}(x_1,...,x_n) \rightarrow \text{output: } \boldsymbol{z}=(z_1,...,z_n) $,其中 \(z_t(1 \le t \le n)\) 为 \(x_t\) 的向量表示
- Decoder:$\text{input}(z_1,...,z_n) \rightarrow \text{output: } \boldsymbol{y}=(y_1,...,y_m) $:一个一个生成(auto-regression),上一时刻输出为下一时刻输入
Encoder
2 个子层:\(LayerNorm(x+Sublayer(x)) * 2\),每一层输出均为 512 维
LN and BN
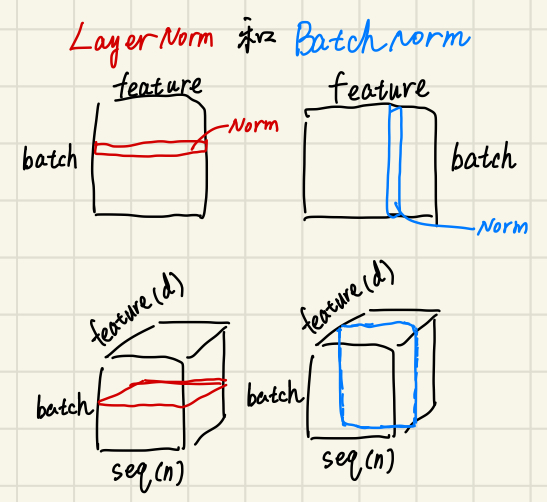
- 如果 feature 长度不同:BN 更加不稳定!

- 预测过程
- BN:要记录全局的 \(\mu\) 和 \(\sigma\),如果有的 feature 很长训练没见过,\(\mu\) 和 \(\sigma\) 就不合适了
- LN:每个样本内部计算,不受全局影响,受长度影响很小
Decoder
3 个字层:\(LayerNorm(x+Sublayer(x)) * 3\),自回归
Attention
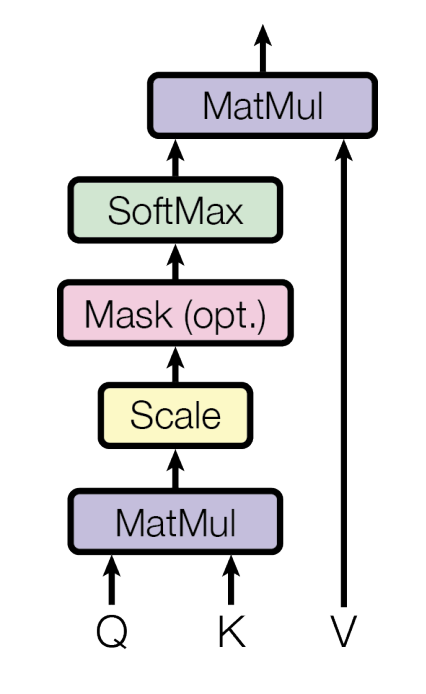
图 2:dot-product attention 结构
其中 \(Q,K\) 是 \(d_k\) 维,\(V\) 是 \(d_v\) 维,attention计算公式:
\[\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V
\]
为什么是 scaled dot-product attention?
- 因为点乘非常简单,两次矩阵乘法易于并行计算
- 当 \(d_k\) 比较大,\(\text{softmax}(QK^T)\) 分布发散,梯度比较小收敛慢
Mask 操作
\(QK^T\) 后将 \(t\) 位置之后变为很小的负数(如\(-1e10\)),softmax 后为 0
Multi-head Attention
能够学习到不同的投影,不同特征。计算公式如下:
\[\text{MultiHead}(Q,K,V)=\text{Concat}(head_1,...,head_n)W^o \\ where \ \ \ head_i=\text{Attention}(QW_i^Q,KW_i^K,VW_i^V)
\]
Feed-Forward
\[\text{FFN}(x)=max(0,xW_1+b_1)W_2+b_2
\]
Postion Encoding
加入时序信息:
\[\text{PE}(pos,2i)=\sin(pos/10000^{2i/d})
\]
\[\text{PE}(pos,2i+1)=\cos(pos/10000^{2i/d})
\]