学期2024-2025-1 学号20241311 《计算机基础与程序设计》第七周学习总结
作业信息
| 这个作业属于哪个课程 | <班级的链接>(2024-2025-1-计算机基础与程序设计(https://edu.cnblogs.com/campus/besti/2024-2025-1-CFAP)) |
|---|---|
| 这个作业要求在哪里 | <作业要求的链接>(2024-2025-1计算机基础与程序设计第七周作业) |
| 这个作业的目标 | <写上具体方面> |
| 作业正文 | ... 本博客链接 |
教材学习内容总结
C语言程序设计第七版第六章循环控制结构学习内容总结
第六章循环控制结构是C语言程序设计中非常重要的一个章节,它涵盖了循环的基本概念、不同类型的循环语句、循环控制语句以及循环在解决实际问题中的应用。以下是该章节学习内容的详细总结:
- 循环的基本概念
循环:在程序中,重复执行一系列语句的过程称为循环。循环是处理重复操作的有效手段,可以简化代码,提高程序的执行效率。
循环体:被重复执行的语句序列称为循环体。 - 循环语句
C语言提供了三种基本的循环语句来实现循环结构:
while语句(当型循环):当指定的条件为真时,重复执行循环体内的语句,直到条件为假时退出循环。其一般形式为:while (条件表达式) { 语句序列 }。
do-while语句(直到型循环):先执行循环体中的语句,然后判断指定的条件是否为真,若为真则继续执行循环体,直到条件为假时退出循环。其一般形式为:do { 语句序列 } while (条件表达式);。注意,do-while循环至少会执行一次循环体。
for语句(当型循环):是一种更为灵活的循环语句,它可以在循环开始前初始化循环控制变量,指定循环条件和循环迭代方式。其一般形式为:for (初始化表达式; 循环条件表达式; 迭代表达式) { 语句序列 }。
3. 循环控制语句
break语句:用于立即退出当前循环(或switch语句),并继续执行循环之后的语句。
continue语句:用于跳过当前循环的剩余语句,并继续下一次循环的迭代。
4. 循环的嵌套
循环可以嵌套使用,即在一个循环体内包含另一个或多个循环语句。嵌套循环的总循环次数等于外层循环次数与内层循环次数的乘积。
5. 循环的应用实例
累加求和:通过循环语句实现一系列数的累加求和。
累乘求积:通过循环语句实现一系列数的累乘求积。
穷举法:通过嵌套循环遍历所有可能的情况,以找到满足条件的解。
迭代求解:通过循环语句迭代更新变量的值,以逼近或求解问题的解。
计算机科学概论学习内容总结
- 算法与数据结构
如果第六章涉及算法与数据结构,那么学习内容可能包括:
算法基础:介绍算法的概念、特性、复杂度分析(时间复杂度和空间复杂度)以及常见算法设计策略(如分治法、动态规划、贪心算法、回溯法等)。
数据结构:详细讲解数组、链表、栈、队列、树、图等基本数据结构的定义、操作及应用场景,并可能涉及哈希表、堆、优先队列等高级数据结构。
2. 低级程序设计语言
如果第六章聚焦于低级程序设计语言,那么学习内容可能包括:
机器语言与汇编语言:介绍计算机底层使用的语言,包括指令集、寻址方式、汇编器的作用等。学生将学习如何编写简单的汇编语言程序,并理解机器语言与高级编程语言之间的转换过程。
伪代码与算法表示:学习如何使用伪代码来描述算法,以及伪代码与高级编程语言之间的关系。伪代码作为一种表达算法思想的工具,有助于理解算法的逻辑结构。
3. 并行计算与多核处理
如果第六章讨论并行计算与多核处理,那么学习内容可能包括:
并行计算基础:介绍并行计算的概念、优势、挑战以及并行算法设计的基本原则。学生将了解如何利用多核处理器实现并行计算,以提高程序的执行效率。
多核处理器编程:探讨在多核处理器上编写高效并行程序的方法和技术,包括线程管理、同步机制、数据共享与保护等。学生将学习如何避免竞态条件、死锁等并发问题,确保并行程序的正确性和稳定性。
4. 计算机体系结构深入
如果第六章深入讨论计算机体系结构,那么学习内容可能包括:
存储系统层次结构:详细分析存储器的不同类型(如缓存、主存、外存)、层次结构及其优化策略。学生将了解存储系统的性能瓶颈及其解决方法,以提高计算机系统的整体性能。
输入输出系统:讲解输入输出设备的原理、接口技术及其在计算机系统中的作用。学生将学习如何设计高效的输入输出系统,以满足不同应用场景的需求。
教材学习中的问题和解决过程(先问 AI)
(一个模板:我看了这一段文字 (引用文字),有这个问题 (提出问题)。 我查了资料,有这些说法(引用说法),根据我的实践,我得到这些经验(描述自己的经验)。 但是我还是不太懂,我的困惑是(说明困惑)。【或者】我反对作者的观点(提出作者的观点,自己的观点,以及理由)。 )
- 问题1:如何利用时间复杂度和空间复杂度来评估算法的性能?
- 问题1解决方案:一、时间复杂度
时间复杂度是衡量算法执行时间随输入规模变化的增长率的一个指标。它通常使用大O符号(O-notation)来表示,这种表示法抽象地描述了算法在最坏情况下的运行时间。
评估方法:
计算基本操作次数:首先,需要确定算法中执行次数最多的基本操作,这通常是循环体内的操作。
忽略低阶项和常数项:在计算时间复杂度时,可以忽略与输入规模n相比增长较慢的低阶项和常数项。
确定最高阶项:只保留与输入规模n相关的最高阶项,并忽略其系数。
常见的时间复杂度类型(按效率从高到低排序):
O(1):常数时间复杂度,算法的执行时间不随输入规模n的变化而变化。
O(log n):对数时间复杂度,算法的执行时间随着输入规模n的增加而对数增长。
O(n):线性时间复杂度,算法的执行时间与输入规模n成正比。
O(n log n):线性对数时间复杂度,常见于高效的排序算法。
O(n^2):平方时间复杂度,常见于简单的排序算法和嵌套循环。
O(n^k)(k为常数):多项式时间复杂度,算法的执行时间与输入规模的幂次成正比。
O(2^n):指数时间复杂度,算法的执行时间随着输入规模n的增加呈指数增长。
O(n!):阶乘时间复杂度,最为低效的算法复杂度,常见于全排列问题的解决方案。
二、空间复杂度
空间复杂度是衡量算法在运行过程中所需内存空间随输入规模变化的增长率的一个指标。它也使用大O符号来表示。
评估方法:
计算额外空间需求:主要关注算法在执行过程中除了输入数据外所需的额外空间。
忽略常数空间:与时间复杂度类似,可以忽略与输入规模n无关的常数空间项。
常见的空间复杂度类型:
O(1):常数空间复杂度,算法所需的额外空间不随输入规模n的变化而变化。
O(n):线性空间复杂度,算法所需的额外空间与输入规模n成正比。
O(n^2):平方空间复杂度,算法所需的额外空间与输入规模的平方成正比。
三、综合评估
在实际应用中,通常需要综合考虑时间复杂度和空间复杂度来评估算法的性能。理想情况下,我们希望算法既能在较短的时间内完成计算,又能占用较少的内存空间。然而,在实际情况下,这两个目标往往存在权衡关系。因此,在选择算法时,需要根据具体问题的需求和约束条件来做出合理的选择。
- 问题2:为什么需要汇编语言?
- 问题2解决方案:汇编语言的存在和需要,主要基于以下几个方面的原因:
与机器语言的桥梁: 汇编语言是一种低级编程语言,它与计算机硬件紧密相关。与机器语言相比,汇编语言采用助记符(mnemonics)来代替二进制指令,使得程序更易于编写和理解。同时,汇编语言能够直接映射到机器指令,因此它能够实现高效的程序执行。
优化性能: 在某些情况下,程序员可能需要直接控制硬件的操作,以实现高效的性能。汇编语言允许程序员编写出针对特定硬件优化的代码,这在需要高性能计算的领域(如游戏开发、实时系统、嵌入式系统等)尤为重要。
细粒度控制: 汇编语言提供了对计算机硬件细粒度的控制,使得程序员能够精确地管理内存使用、处理器寄存器和其他硬件资源。这种控制级别在高级语言中通常无法实现,因为高级语言更倾向于提供抽象和通用的编程模型。
理解计算机底层原理: 学习汇编语言有助于程序员深入理解计算机的底层原理,包括指令集架构、内存管理、处理器工作方式等。这种理解对于编写高效、可靠的代码至关重要,也有助于程序员在调试和优化程序时更准确地定位问题。
历史遗留和兼容性: 汇编语言在计算机科学的发展历程中扮演了重要角色。许多早期的计算机系统和软件都是用汇编语言编写的,因此了解汇编语言对于维护和更新这些系统至关重要。此外,某些领域(如嵌入式系统)中,由于硬件和软件的兼容性要求,汇编语言仍然被广泛使用。
特定需求: 在某些特定应用场景下,如编写启动代码、操作系统内核、设备驱动程序等,汇编语言是不可或缺的。这些场景通常需要对硬件进行直接操作,而汇编语言提供了这种能力。
综上所述,汇编语言的存在和需要是基于其对硬件的直接控制、性能优化、细粒度管理、底层原理理解以及历史遗留和兼容性等多方面的考虑。尽管高级语言在编程效率和可读性方面更具优势,但汇编语言在计算机科学和工程领域仍然占据着重要地位。
基于AI的学习
我正在学习循环控制结构与循环语句的知识点请你以苏格拉底的方式对我进行提问一次一个问题
Kimi(moonshot-v1-8k)
很好,让我们开始苏格拉底式的对话。我会逐步提出问题,帮助你深入思考循环控制结构与循环语句的知识点。
问题1: 你能描述一下什么是循环控制结构吗?
对一些操作进行重复操作
Kimi(moonshot-v1-8k)
问题2: 那么,这种重复操作在编程中解决了什么问题?
允许用户连续多次进行操作
Kimi(moonshot-v1-8k)
问题3: 当我们谈到“允许用户连续多次进行操作”时,你认为循环控制结构是如何实现这一功能的?
重复执行一些操作
Kimi(moonshot-v1-8k)
问题4: 你能否具体说明,在编程中哪些场景下会需要“重复执行一些操作”?
级数求和、穷举、迭代求和
Kimi(moonshot-v1-8k)
问题5: 在级数求和、穷举、迭代求和这些场景中,循环控制结构是如何帮助我们高效地处理问题的?你能描述一下循环在这些场景中的具体应用吗?
这个问题将帮助你思考循环控制结构在解决实际问题中的应用。通过具体的例子,我们可以更好地理解循环的工作原理和优势。如果你有任何想法或疑问,请随时分享!
请你讲讲
Kimi(moonshot-v1-8k)
当然,让我们探讨循环控制在级数求和、穷举和迭代求和中的应用。
级数求和
级数求和通常涉及到对一系列数值进行累加。例如,计算前n个自然数的和。在这种情况下,循环允许我们重复执行加法操作,直到处理完所有的项。
示例代码(Python):
Python
复制
sum = 0
n = 100 # 假设我们要计算前100个自然数的和
for i in range(1, n + 1):
sum += i
print("前100个自然数的和是:", sum)
在这个例子中,for循环用于重复执行加法操作100次,每次将当前的索引i加到变量sum上。
穷举
穷举是一种通过尝试所有可能的情况来寻找解决方案的方法。循环在穷举中扮演着关键角色,它允许我们遍历所有可能的选项。
示例代码(Python):
Python
复制
def find_solution():
for i in range(1, 101): # 假设我们在1到100之间寻找一个条件满足的解
if is_solution(i): # 假设is_solution是一个检查条件是否满足的函数
return i
return None
def is_solution(x):
# 一些检查条件的逻辑
return x % 5 == 0 # 例如,找到一个能被5整除的数
在这个例子中,for循环用于遍历1到100之间的所有数字,直到找到一个满足条件的解。
迭代求和
迭代求和涉及到逐步累加一系列数值。这与级数求和类似,但更强调逐步处理和累加的过程。
示例代码(Python):
Python
复制
def iterative_sum(n):
sum = 0
for i in range(1, n + 1):
sum += i
return sum
result = iterative_sum(100)
print("前100个自然数的和是:", result)
在这个例子中,for循环用于逐步累加从1到n的所有数字,每次迭代都将当前的索引i加到变量sum上。
通过这些例子,我们可以看到循环控制在处理级数求和、穷举和迭代求和等场景中的重要性。循环允许我们以简洁、高效的方式重复执行操作,从而解决各种计算和搜索问题。
三个原则:
- 切勿原封不动地接受生成式人工智能工具的输出;确保对其进行评估、完善和修改(或提示),以适应您的目标。
- 切勿将任何个人数据(自己、同学、老师等)或版权材料纳入到你的提示词中。这个可以说是保护个人隐私的最起码的举措。
- 所有人工智能生成工具都容易产生幻觉,因此会生成不准确或误导性的信息,要学会甄别信息真假
选择至少2个知识点利用chatgpt等工具进行苏格拉底挑战,并提交过程截图,提示过程参考下面内容
“我在学***X知识点,请你以苏格拉底的方式对我进行提问,一次一个问题”
核心是要求GPT:“请你以苏格拉底的方式对我进行提问”
然后GPT就会给你提问,如果不知道问题的答案,可以反问AI:“你的理解(回答)是什么?”
如果你觉得差不多了,可以先问问GPT:“针对我XXX知识点,我理解了吗?”
GPT会给出它的判断,如果你也觉得自己想清楚了,可以最后问GPT:“我的回答结束了,请对我的回答进行评价总结”,让它帮你总结一下。
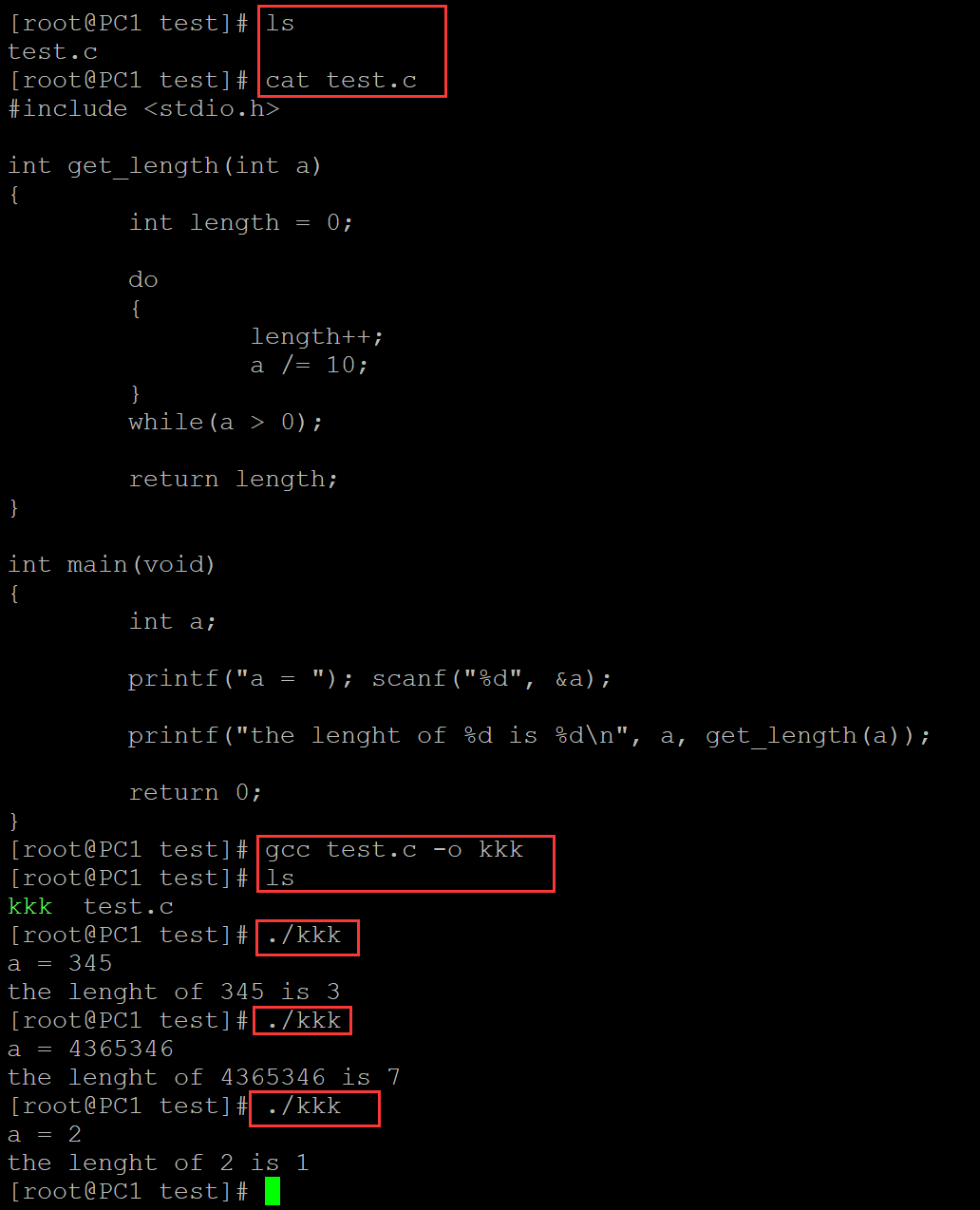
代码调试中的问题和解决过程
- 问题1:无法计算字符长度
- 问题1解决方案:使用strlen函数同时加入string.h头文件
- 问题2:无法选择某个具体字符
- 问题2解决方案:使用数组【】
- ...
代码托管
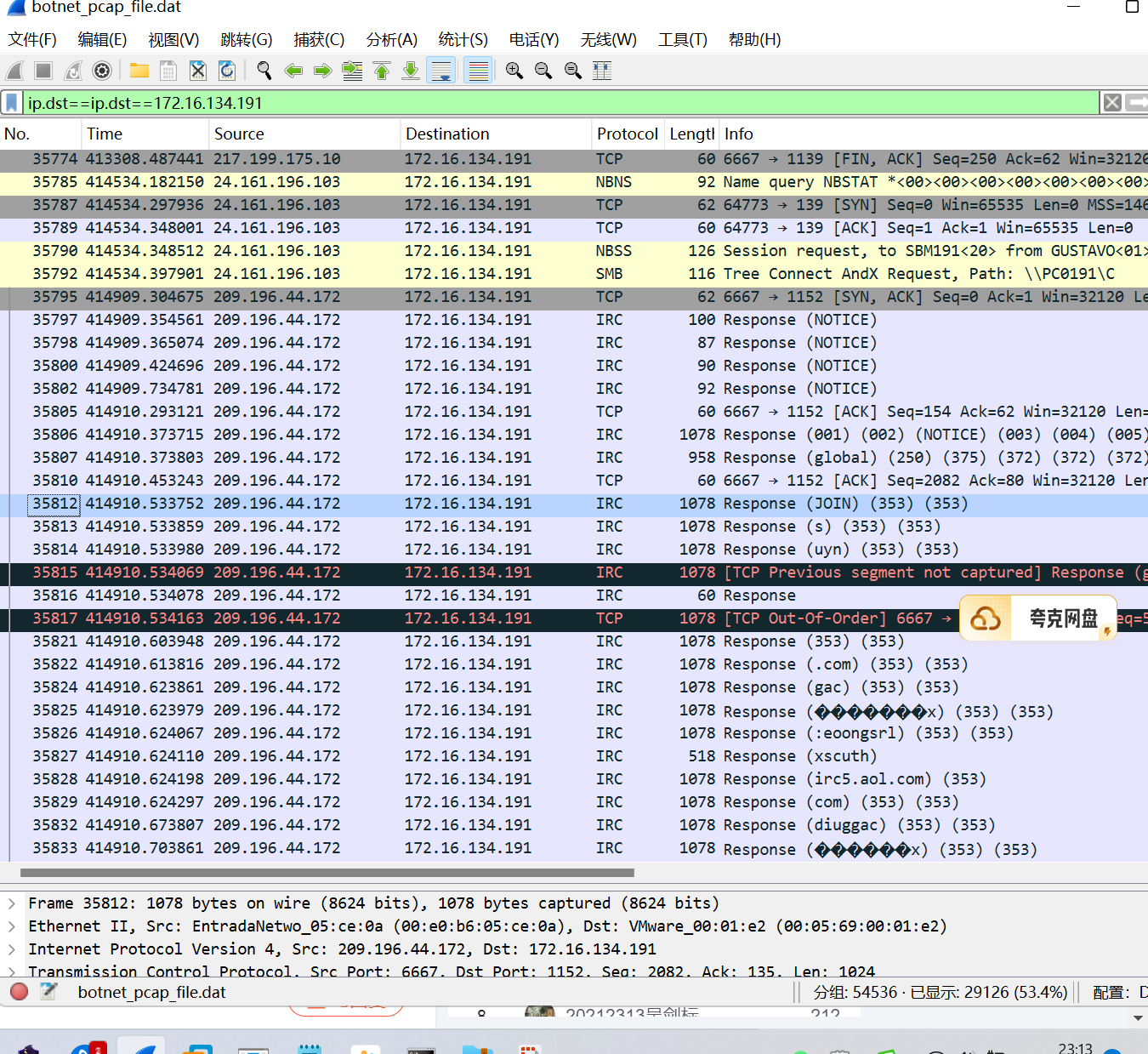
(statistics.sh脚本的运行结果截图)
上周考试错题总结
无
其他(感悟、思考等,可选)
菜就多练
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 500/1000 | 3/7 | 22/60 | |
| 第四周 | 300/1300 | 2/9 | 30/90 | |
| 第五周 | 900/1300 | 2/9 | 30/90 | |
| 第六周 | 1000/1300 | 2/9 | 30/90 | |
| 第七周 | 1000/1300 | 2/9 | 30/90 | |
| 尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。 | ||||
| 耗时估计的公式 | ||||
| :Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。 |
参考:软件工程软件的估计为什么这么难,软件工程 估计方法
-
计划学习时间:XX小时
-
实际学习时间:XX小时
-
改进情况:
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)
参考资料
- 《计算机科学概论(第七版)》
- ...