树形 DP 中的换根 DP 问题又被称为二次扫描,通常需要求以每个点为根时某个式子的答案。
这一类问题通常需要遍历两次树,第一次遍历先求出以某个点(如 \(1\))为根时的答案,在第二次遍历时考虑由根为 \(u\) 转化为根为 \(v\) 时答案的变化(换根)。这个变化往往分为两部分,\(v\) 子树外的点到 \(v\) 相比于到 \(u\) 会增加一条边,而 \(v\) 子树内的点到 \(v\) 相比于到 \(u\) 会减少一条边。
所以往往在第一次遍历时可以顺带求出一些子树信息,利用这些信息辅助第二次遍历时的换根操作。
经典例题:求对于每个点而言,其他点到这个点的距离之和。
例题:P3478 [POI2008] STA-Station
给定一棵 \(n\) 个节点的树,求出一个节点,使得以这个节点为根时,所有节点的深度之和最大。
数据范围:\(n \le 10^6\)。
分析:随便选择一个节点 \(u\) 作为根节点,遍历整棵树,则得到了以 \(u\) 为根节点时的深度之和。
令 \(dp_u\) 表示以 \(u\) 为根时,所有节点的深度之和。设 \(v\) 为当前节点的某个子节点,考虑“换根”,即以 \(u\) 为根转移到以 \(v\) 为根,显然在换根的过程中,以 \(v\) 为根会导致每个节点的深度都产生改变。具体表现为:
- 所有在 \(v\) 的子树上的节点深度都减少了一,那么总深度和就减少了 \(sz_v\),这里用 \(sz_i\) 表示以 \(i\) 为根的子树中的节点个数。
- 所有不在 \(v\) 的子树上的节点深度都增加了一,那么总深度和就增加了 \(n - sz_v\)。
根据这两个条件就可以推出状态转移方程:\(dp_v = dp_u + n - 2 \times sz_v\),因此可以在第一次遍历时顺便计算一下 \(sz\),第二次遍历时用状态转移方程计算出最终的答案。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1000005;
vector<int> tree[N];
int sz[N], res, n;
LL ans;
void dfs(int cur, int fa, int depth) {ans += depth;sz[cur] = 1;for (int to : tree[cur]) {if (to == fa) continue;dfs(to, cur, depth + 1);sz[cur] += sz[to];}
}
void solve(int cur, int fa, LL sum) {for (int to : tree[cur]) {if (to == fa) continue;LL tmp = sum + n - 2 * sz[to];if (tmp > ans) {ans = tmp; res = to;}solve(to, cur, tmp);}
}
int main()
{scanf("%d", &n);for (int i = 1; i < n; i++) {int u, v; scanf("%d%d", &u, &v);tree[u].push_back(v); tree[v].push_back(u);}dfs(1, 0, 1);res = 1;solve(1, 0, ans);printf("%d\n", res);return 0;
}
习题:P2986 [USACO10MAR] Great Cow Gathering G
解题思路
与上一题类似,只不过这题换根时的变化量是点权和(即牛棚中奶牛的数量)的变化乘以边权。
参考代码
#include <cstdio>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 100005;
int n, c[N];
LL ans;
struct Edge {int to, l;
};
vector<Edge> tree[N];
void dfs(int cur, int fa, int depth) {ans += 1ll * depth * c[cur];for (Edge e : tree[cur]) {if (e.to == fa) continue;dfs(e.to, cur, depth + e.l);c[cur] += c[e.to];}
}
void solve(int cur, int fa, LL sum) {for (Edge e : tree[cur]) {if (e.to == fa) continue;LL tmp = sum + 1ll * (c[1] - 2 * c[e.to]) * e.l;ans = min(ans, tmp);solve(e.to, cur, tmp);}
}
int main()
{scanf("%d", &n);for (int i = 1; i <= n; i++) scanf("%d", &c[i]);for (int i = 1; i < n; i++) {int a, b, l; scanf("%d%d%d", &a, &b, &l);tree[a].push_back({b, l}); tree[b].push_back({a, l});}dfs(1, 0, 0);solve(1, 0, ans);printf("%lld\n", ans);return 0;
}
例题:P3047 [USACO12FEB] Nearby Cows G
分析:可以先对树做一次遍历得到每个节点对应的子树下距离子树根节点距离 \(0 \sim x\) 之间的点权和,
然后考虑每个点距离 \(k\) 之内的点权和。子树下的点权和在第一次遍历时已经计算完成,因此还需要计算的是在该点子树外的距离 \(k\) 以内的部分,而这个部分可以通过对该点上方最多 \(k\) 个祖先节点的处理,如下图所示。
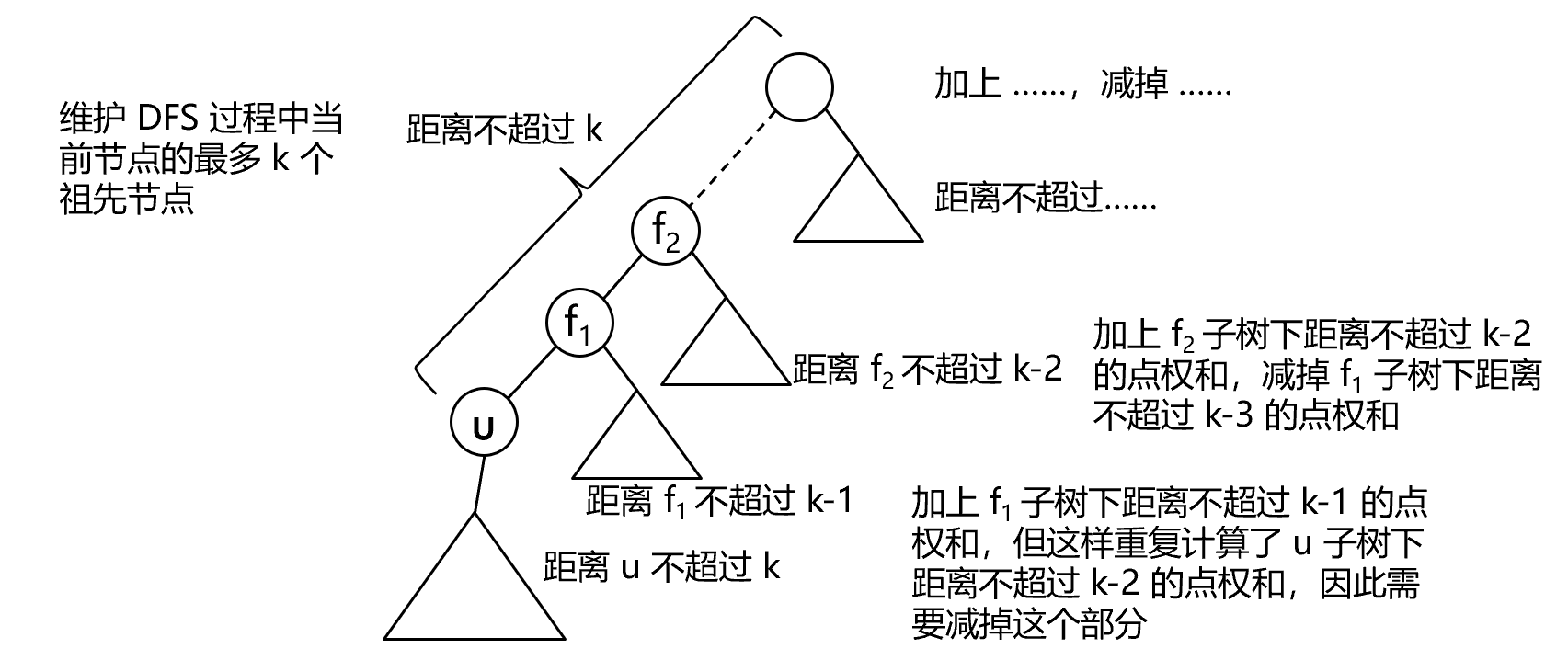
参考代码
#include <cstdio>
#include <vector>
using std::vector;
const int N = 100005;
const int K = 25;
vector<int> tree[N];
int n, k, sum[N][K], c[N], ans[N];
void dfs(int u, int fa) {for (int v : tree[u]) {if (v == fa) continue;dfs(v, u);for (int i = 1; i <= k; i++) {sum[u][i] += sum[v][i - 1];}}sum[u][0] = c[u];
}
void calc(int u, int fa, vector<int> pre) {int dis = pre.size();pre.push_back(u);// u的子树内的距离范围内的点权和ans[u] = sum[u][k];// 计算u的子树外的距离范围内的点权和for (int i = 0; i + 1 < pre.size(); i++) {int cur = pre[i], nxt = pre[i + 1];// 对于边cur->nxtans[u] += sum[cur][k - dis]; // 加上cur子树下的距离内点权和if (k - dis > 0) ans[u] -= sum[nxt][k - dis - 1]; // 减去nxt子树下刚刚被重复计算的部分dis--;}vector<int> path;if (pre.size() == k + 1) {// pre[0]即将超出下面的点的距离范围k,要被淘汰for (int i = 1; i < pre.size(); i++) path.push_back(pre[i]);} else path = pre;for (int v : tree[u]) {if (v == fa) continue;calc(v, u, path);}
}
int main()
{scanf("%d%d", &n, &k);for (int i = 1; i < n; i++) {int u, v; scanf("%d%d", &u, &v);tree[u].push_back(v); tree[v].push_back(u);}for (int i = 1; i <= n; i++) scanf("%d", &c[i]);dfs(1, 0);// 生成前缀和for (int i = 1; i <= n; i++) {for (int j = 1; j <= k; j++) sum[i][j] += sum[i][j - 1];}vector<int> tmp;calc(1, 0, tmp);for (int i = 1; i <= n; i++) printf("%d\n", ans[i]);return 0;
}