CF1945A
贪心简单题
先把b自己内部组合,再考虑与c组合
CF1945B
简单题数学题
因为在0m的时间内一定能覆盖所有的情况,所以对0m的时间内最多烟花数进行小学2年纪计算即可
CF1945C
简单题
枚举每一个断点,记录答案即可
CF1945D
挺好玩的一道贪心题。
转化一下式子,我们发现 \(a[i],b[i]\) 的选择过程类似于一个上下反复横跳的最终的选取停止在 \(a\) 数组的一个过程,如下图。
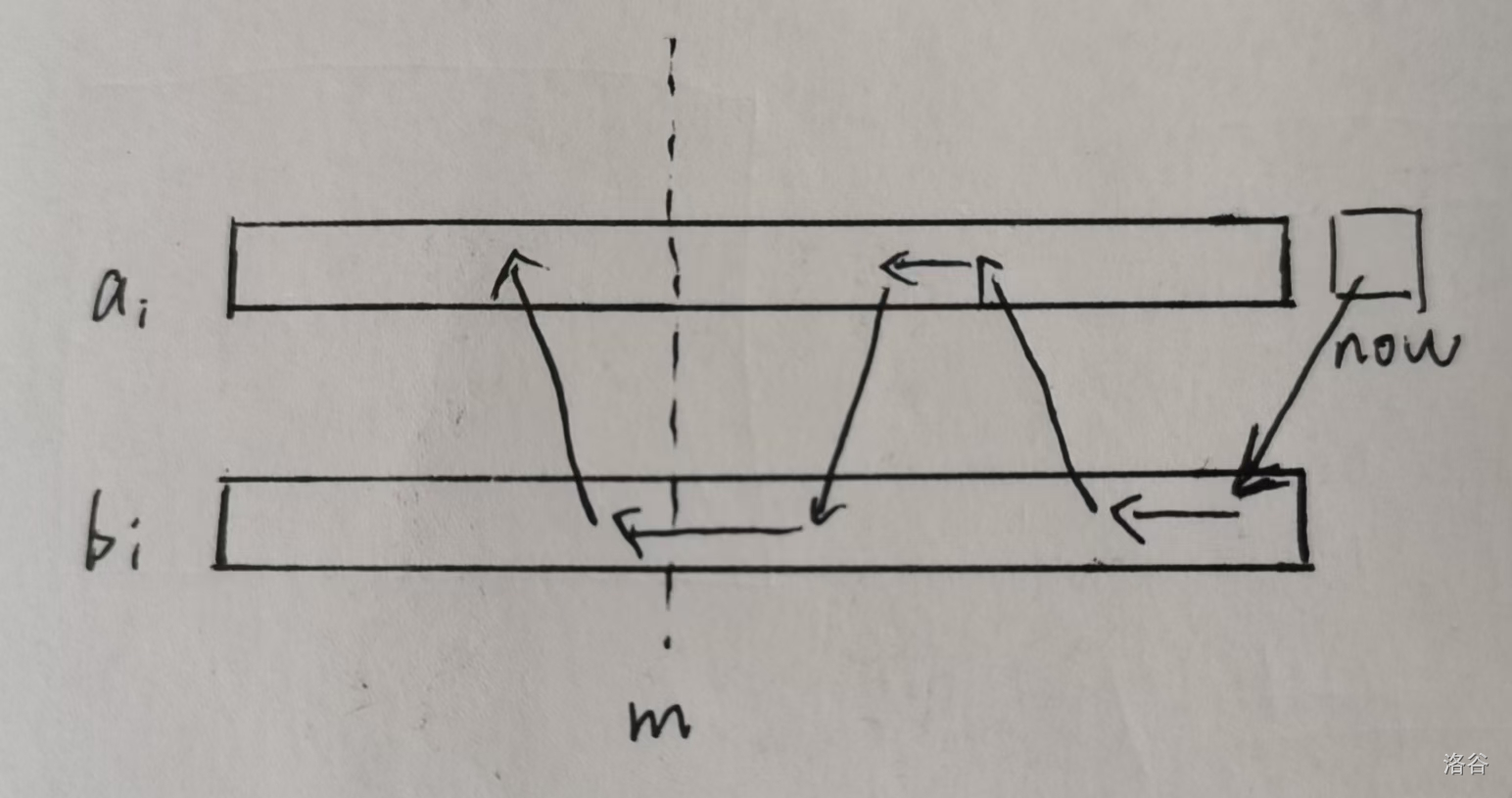
注意到对于一个 \(j\) 位置,我们只会在 \(a[j]\),\(b[j]\) 中选一个对答案产生贡献,且在 \(m+1,m+2,\cdots, n\) 之间选哪一个数并不会对之后的决策产生影响(无后效性)。
因为在 \(m+1,m+2,\cdots, n\) 之间我们每个选择是独立的,所以在 \(m+1,m+2,\cdots, n\) 之间直接贪心,对答案的贡献即为 \(\sum_{i=m+1}^n \min\{a[i],b[i]\}\)。
那么在 \(1,2,\cdots,m\) 这一段对答案的贡献就显而易见了,因为在这一段中只要选择了 \(a[j]\) 就停止选择了,所以答案的组成既是一段 \(b_{j+1},b_{j+2} ,\cdots ,b_m\) 再加上 \(a_j\)。
所以只需要统计一下 \(\min_{i=1}^m\{\sum_{j=i+1}^mb[j]+a[i]\}\) 即可
最终答案即是这两段贡献的加和
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5,inf=1e18+5;
int n,m,t;
int a[N],b[N];
signed main(){scanf("%lld",&t);while(t--){scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}for(int i=1;i<=n;i++){scanf("%lld",&b[i]);}int cnt=0,ans=inf;for(int i=n;i>=1;i--){if(i>m){if(a[i]>b[i]){cnt+=b[i];}else{cnt+=a[i];}}else{ans=min(ans,cnt+a[i]);cnt+=b[i];}}printf("%lld\n",ans);}
}