连通性问题
-
点双连通:在无向图中,删除一个点(不是 \(x\) 或者 \(y\))后,点 \(x\) 和点 \(y\) 仍然能够彼此到达,那么称 \(x\) 和 \(y\) 是点双连通的。
-
边双连通:在无向图中,删除一条边后,点 \(x\) 和点 \(y\) 仍然能够彼此到达,那么称 \(x\) 和 \(y\) 是边双连通的。
性质
-
点双连通不具有传递性,但边双连通具有。
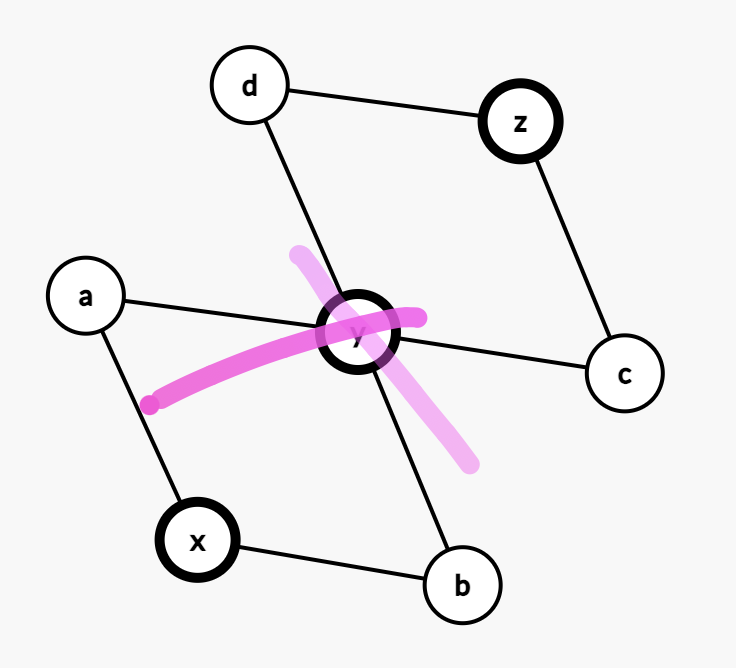
如图,但 \(y\) 被删去之后,虽然 \(x,y\) 以及 \(y,z\) 都是点双连通的,但是 \(x,z\) 却不是点双连通的了。
边双连通具有传递性是因为无论删哪条边 \(x,y\) 和 \(y,z\) 都是边双连通的(由定义易知),这也就是说 \(x,z\) 是边双连通的。
割点
性质:
-
至少三个点的图中才有割点。(易证)
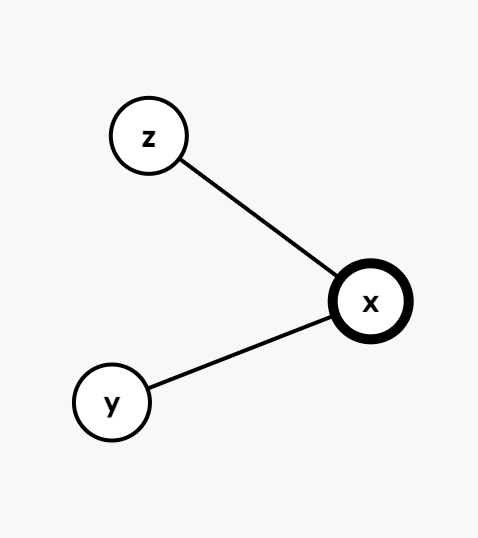
如图,\(x\) 即为该图的割点。
判定:
若搜索树中,有从 \(x\) 到 \(y\) 的连边,当 \(low_y \ge dfn_x\) 时(定义同 tarjan 算法),说明 \(y\) 能到达的最小时间戳是 \(x\) 的时间戳,即 \(y\) 被 \(x\) 与 \(x\) 之前的结点「隔开」, 因此 \(x\) 可能是割点。
只要 \(x\) 不是搜索树的根结点,或者 \(x\) 是根结点 且 \(x\) 的子结点大于 \(1\) 个,那么 \(x\) 就是割点。
P3388 & UVA10199
板子。
code
#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
int n,m,cnt,rt;
vector<int> G[N],ans;
int dfn[N],low[N];
bool cut[N];void tarjan(int cur){dfn[cur]=low[cur]=++cnt;int num=0;for(int i:G[cur]){if(!dfn[i]){tarjan(i);low[cur]=min(low[cur],low[i]);++num;if(low[i]>=dfn[cur]&&(cur!=rt||num>1)){cut[cur]=1;}}else{low[cur]=min(low[cur],dfn[i]);}}
}int main(){ios::sync_with_stdio(0);cin.tie(0);cin>>n>>m;for(int i=1,u,v;i<=m;i++){cin>>u>>v;G[u].push_back(v);G[v].push_back(u);} for(int i=1;i<=n;i++)if(!dfn[i])rt=i,tarjan(i);for(int i=1;i<=n;i++)if(cut[i])ans.push_back(i);cout<<ans.size()<<'\n';for(int i:ans)cout<<i<<' ';return 0;
}
CF22C
构造题,从简单情况开始考虑。
首先 \(m\) 必须 \(\ge n-1\),否则图不可能联通。
当 \(m=n-1\) 时,显然让 \(v\) 作为根,其他点直接向 \(v\) 连边是最简单的方案,其他方案都可以通过改变树的形态的方式使得其与此方案等价。
接着,当 \(m>n-1\) 时,为了使添加的边尽可能多,我们只能孤立出一个子节点,其他的 \(n-2\) 个子节点连出完全图即可。
于是 \(m\) 的上界即为 \(n-1+\frac{(n-2) \times (n-3)}{2}\),做完了。
code
//
// CF22C.cpp
//
//
// Created by _XOFqwq on 2024/11/7.
//#include <bits/stdc++.h>
using namespace std;int n,m,v;void print(int x){for (int i=1; i<=n; i++) {if (!m) {return;}if (i!=v&&i!=x) {for (int j=i+1; j<=n; j++) {if (!m) {return;}if (j!=v&&j!=x) {cout<<i<<' '<<j<<'\n',m--;}}}}
}int main(){ios::sync_with_stdio(0);cin.tie(0);cin>>n>>m>>v;if (m<n-1||m>n-1+(n-2)*(n-3)/2) {cout<<-1;} else {for (int i=1; i<=n; i++) {if (i!=v) {cout<<v<<' '<<i<<'\n';}}m-=n-1;if (v==n) {print(n-1);} else {print(n);}}return 0;
}
P3469
容易发现每个点都有一个基础贡献 \(2 \times (n-1)\),只有割点才会产生额外贡献。
对于割点,将它提起来作为根,于是有子树内的联通块和子树外的联通块。子树内的贡献算两次,单点算两次,然后子树外的再算两次即可。具体见代码实现。
code
//
// P3469.cpp
//
//
// Created by _XOFqwq on 2024/11/7.
//#include <bits/stdc++.h>
#define int long long
using namespace std;const int N=5e5+5;
int n,m,cnt,rt;
int siz[N],ans[N];
bool cut[N];
int dfn[N],low[N];
vector<int> G[N];void tarjan(int cur){dfn[cur]=low[cur]=++cnt;siz[cur]=1;int num=0,sum=0;for (int i : G[cur]) {if (!dfn[i]) {tarjan(i);siz[cur]+=siz[i];low[cur]=min(low[cur],low[i]);num++;if (low[i]>=dfn[cur]&&(cur!=rt||num>1)) {sum+=siz[i];ans[cur]+=siz[i]*(n-siz[i]); //子树内两次 + 子树外一次 + 子树内与单点cut[cur]=1;}} else {low[cur]=min(low[cur],dfn[i]);}}if (cut[cur]) {ans[cur]+=(n-sum-1)*(sum+1)+n-1; //子树外一次 + 子树外与单点 + 一次单点} else {ans[cur]=2ll*(n-1);}
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cin>>n>>m;for (int i=1,u,v; i<=m; i++) {cin>>u>>v;G[u].push_back(v);G[v].push_back(u);}rt=1,tarjan(1);for (int i=1; i<=n; i++) {cout<<ans[i]<<'\n';}return 0;
}