基本内容
- 入门例子 USACO06NOV] Corn Fields G - 洛谷 | 计算机科学教育新生态
题目简述:在一个\(N\times M\)的玉米田中种玉米,有一些坏掉的土地是不能种玉米的,另外相邻的两个田也不可以种,一共有多少种种植方案(荒地也算一种),如图所示,由于相邻的土地不能种植,此时一号土地已经不能种植
- 暴力解法
每一行的玉米田有\(2^M\)种种植状态,再加上每一行的状态搜索,共有\(2^{M+N}\)种状态,并且还需要判断该状态是否合法,时间复杂度非常高。
- 只考虑一行玉米田状态
由于每一行的状态都是\(2^M\)种,并且可以种植的满足条件一致: ① 坏田不能种植 ② 相邻的田不能种植
首先只考虑相邻田不能种植的情况 ① 坏田不能种植 ,可以发现,若只考虑玉米田只有一行的情况下,每一行的满足状态都是一样的,因此,可以先对不满足的种植状态去除。当我们用 0,1 表示田地的种植状态时,M列的玉米田可表示一个M位二进制数。例如该状态可以表示为二进制数 101,即为5,通过一个十进制数来表示当前行玉米田的状态。在遍历状态时可以减少运算效率。

def check(x):for i in range(m): if (x >> i & 1) & (x >> (i + 1) & 1): #(位运算,若为1则表示有相邻的玉米田种植,不满足状态)return Falsereturn True
- 考虑多行玉米田状态
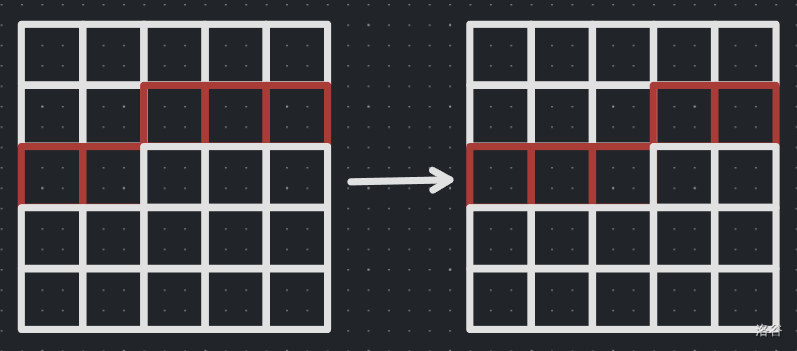
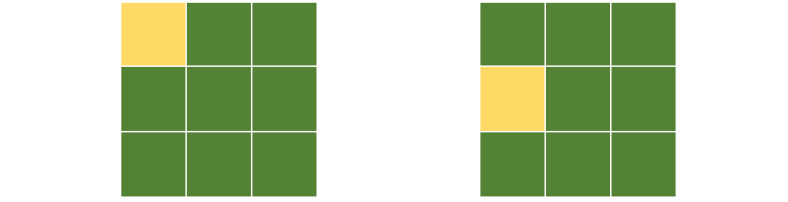
由于受到相邻田不能种植的条件影响,当第\(i-1\)行\(M\)列的玉米田被种植时,第\(i\)行\(M\)列就无法被种植,可以发现每一行的状态只受到上一行状态的影响,并且当\(i-1\)行的状态确定时,第\(i\)行的状态数目也确定了,这也就是状态压缩DP的关键,将多行的状态变换用一个状态转移的方式表示出来。如图所示,左图第一行的种植状态是100,第二行可以满足的数目是3;由于右图第二行的种植状态与其一致,因此右图第三行的满足数目也是3,
将第\(i-1\)行的状态设为\(a\),第\(i\)的状态设为\(b\),满足状态的代码如下所示:
# states 存储的是玉米田只有一行时的满足状态
# heads 一个字典,存储某一个状态可以转化为下一行的全部状态
for i in range(len(states)):for j in range(len(states)):a, b = states[i], states[j]if (a & b) == 0: # 表示上下没有相邻的1,若有,则会出现某一位二进制位为1,不为0heads[a].append(b) # 将b的状态加入到a的满足状态中
- 坏田不能种植
当分析完相邻的田不能种植条件后,还需要分析坏田不能种植的情况,相对于上面的状态转移,这种情况较好分析,只需要满足当前行玉米田的坏田状态与当前状态是否有同时为1的列即可,若有则当前状态不满足,若无则满足,该条件判断与判断相邻行是否同时种植一致
- 解题代码
M, N = map(int, input().split())
data = [list(map(int, input().split())) for _ in range(M)]
g = [(~int("".join(map(str, row)), 2)) & ((1 << N) - 1) for row in data] # 取反
mod = 100000000
g.append(1 << N)def check(x):for i in range(N): if (x >> i & 1) & (x >> (i + 1) & 1): # 位运算,若有相邻的玉米田种植,不满足状态return Falsereturn True
heads = {}
states = []
for i in range(1 << N):if check(i):states.append(i)heads[i] = []for i in range(len(states)):for j in range(len(states)):a, b = states[i], states[j]if (a & b) == 0: # 表示上下没有相邻的1,若有,则会出现某一位二进制位为1,不为0heads[a].append(b) # 将b的状态加入到a的满足状态中
f = [[0 for _ in range(1 << N)]for _ in range(M + 2)]
f[0][0] = 1
for i in range(1, M+2): #本来是遍历到M即可,但遍历到M+1时可以在最后输出的时候直接取0状态即为前M层的最大数量for a in states:if g[i-1] & a:continuefor b in heads[a]:f[i][a] = (f[i][a] + f[i-1][b]) % mod
print(f[M+1][0])
题目
- N皇后问题
题目与玉米田的思路基本一致,多了一个判断问题,即对角的国王也会相互攻击,为了加入此情况,在状态转移的判断条件上需要加入对角判断的处理

- 状态满足代码修改
for i in range(len(states)):for j in range(len(states)):a, b = states[i], states[j]if (a & b) == 0 and check(a | b):# 只需在这部分上加入check(a | b),因为对角没有互相攻击即为交集没有相邻的两个皇后heads[a].append(b)