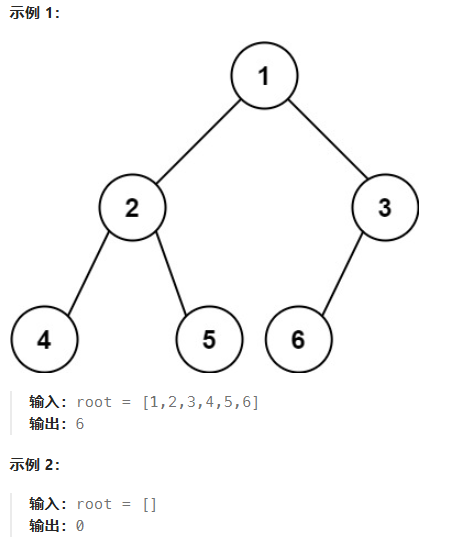
思路
一、层序遍历,时间复杂度O(n)
二、利用完全二叉树性质,时间复杂度O(logn * logn)(小于O(n))
完全二叉树性质:若树深度为h,则前h-1层节点都达到最大值。第h层节点都集中在最左侧的位置
完全二叉树要么1.是满二叉树 2.最后一层没满
-
满二叉树计算节点数太方便了,直接用公式2^h-1。
-
最后一层没满则遍历根的左右子树,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算
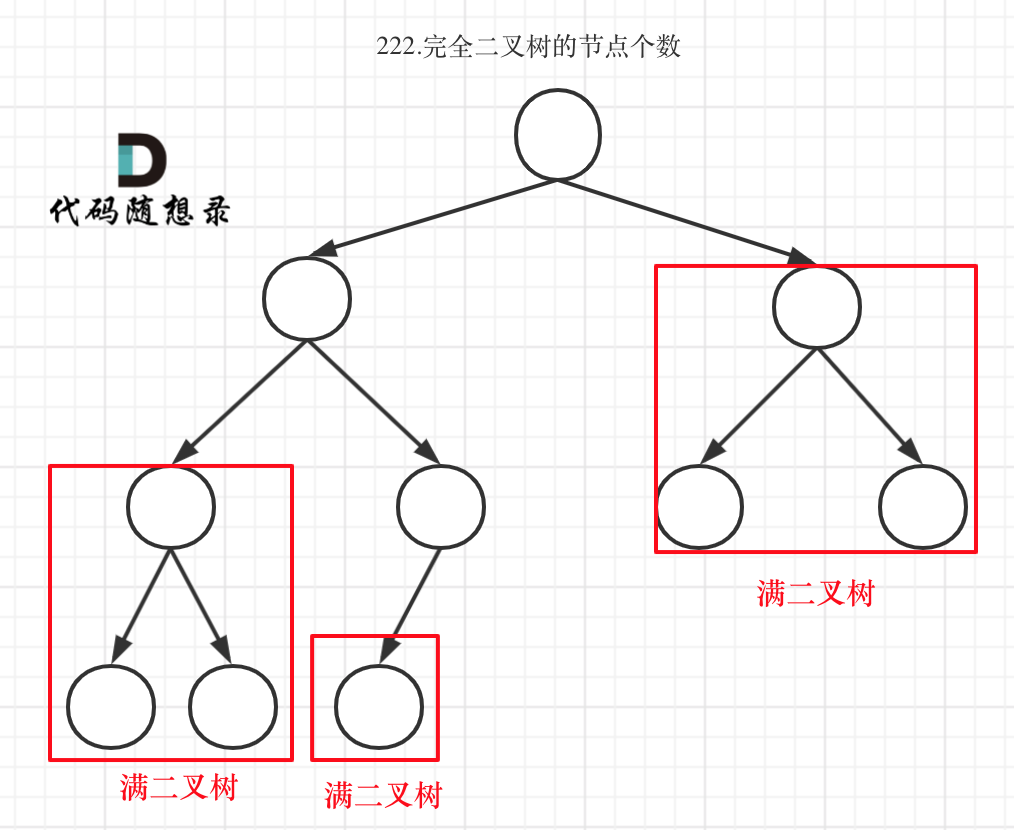
那么现在的问题就是怎么判断一棵树是否是满二叉树:在完全二叉树中,若左右子树的深度一样则为满二叉树
代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int countNodes(TreeNode* root) {//1.终止条件if(root == nullptr)return 0;//2.中间代码int lheight=0,rheight=0;TreeNode* lnode = root->left,*rnode = root->right;while(lnode != nullptr){ //左子树深度lheight++;lnode = lnode->left;}while(rnode != nullptr){ //右子树深度rheight++;rnode = rnode->right;}if(lheight == rheight){return (2 << lheight) - 1; //用位运算代替幂,速度更快}return countNodes(root->left) + countNodes(root->right) + 1;}
};
总结
本题难点在于怎么利用完全二叉树性质,对于满二叉树用公式计算节点很容易想到,但想到非满二叉树可以递归直到找到有左右子树是满二叉树则不容易。而利用完全二叉树性质判断满二叉树也是第一次见。
此外还要分析清楚递归的三大条件(递归函数,终止条件和单层递归逻辑),树的遍历顺序(左右中,后序遍历)