题意:
给定长度为 \(N\) 的序列 \(a\),求满足以下条件的 \((l,r)\) 对数:
-
\(1\le l\le r\le N\);
-
\(a_l,a_{l+1},\cdots,a_{r-1},a_r\) 是 \(1\sim r-l+1\) 的排列。
-
\(1\le N\le 10^6\);\(1\le a_i\le N\)。
思路
-
首先,“排列”本身这个性质是很强的。因为排列本身需要从1开始,因此排列的数目必定不会很多。
同时,只要我们知道了排列中最大的数,我们就知道了这个排列的长度。 -
因此考虑去找区间中最大的数,然后去枚举区间的范围。在这个区间中,我们其实就将问题转化为了区间内的数的种类。只不过这里种类必须为区间长度。
这种问题有一个很经典的转化,即维护一个数上一个与其值相同的数出现的位置,然后线段树去统计。
不过这道题并不需要,因为我们只需要判断种类数是不是 \(n\) 就行了,因此可以用st表 \(O(1)\) 判断,只需要区间内所有数上一次出现的位置都小于区间左端点就行了。 -
处理完最大值后就可以继续向两边递归去找。
复杂度
- 这里的时间复杂度与启发式合并比较类似,平摊下来总体是 \(O(nlogn)\) 的。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+7;
int n,a[N],g[N][20],lst[N],lg[20];long long ans=0;
struct node
{int val,loc;
}f[N][20];
node maxx(node x,node y){return x.val>=y.val?x:y;}
void init()
{lg[0]=-1;for(int i=1;i<=n;i++) lg[i]=lg[i/2]+1;for(int i=1;(1<<i)<=n;i++)for(int j=1;j+(1<<i)-1<=n;j++)f[j][i]=maxx(f[j][i-1],f[j+(1<<(i-1))][i-1]),g[j][i]=max(g[j][i-1],g[j+(1<<(i-1))][i-1]);
}
node fmax(int l,int r){int x=lg[r-l+1];return maxx(f[l][x],f[r-(1<<x)+1][x]);}
int gmax(int l,int r){int x=lg[r-l+1];return max (g[l][x],g[r-(1<<x)+1][x]);}
bool query(int l,int r){return gmax(l,r)<l;}
void solve(int l,int r)
{if(r<l) return;if(l==r) {ans+=(a[l]==1);return;}node mval=fmax(l,r);if(mval.loc-l<=r-mval.loc) for(int i=max(l,mval.loc-mval.val+1),j=i+mval.val-1;i<=mval.loc&&j<=min(r,mval.loc+mval.val-1);++i,++j) ans+=query(i,j);else for(int j=mval.loc,i=j-mval.val+1;i<=mval.loc,j<=min(r,mval.loc+mval.val-1);++i,++j) if(i<l) continue;else ans+=query(i,j);solve(l,mval.loc-1),solve(mval.loc+1,r);
}
int main()
{ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++) {cin>>a[i];f[i][0]={a[i],i},g[i][0]=lst[a[i]],lst[a[i]]=i;}init();solve(1,n);cout<<ans<<'\n';return 0;
}
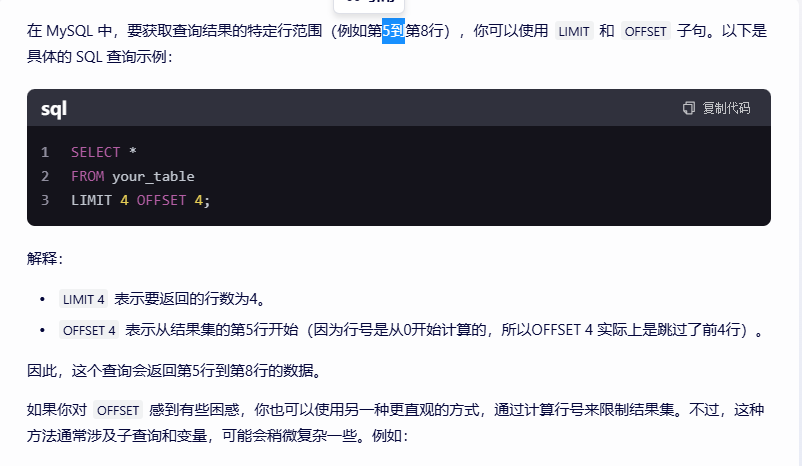


![[自用]ubuntu下kafka环境的搭建](https://img2024.cnblogs.com/blog/1745587/202411/1745587-20241113151546659-2131576447.png)