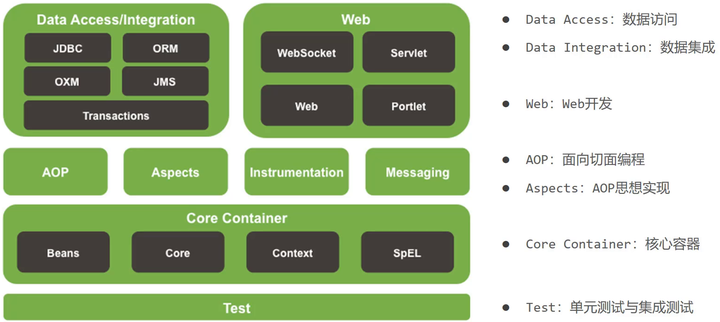
1.实现

答：至少需要比7次。

1. 25匹马随机分成5组，每组比赛一次也即总共比5次先看一下每组马的快慢情况。

我们一开始并不知道这25匹马中谁快谁慢，所以需要筛选出那些跑的较快的马出来去竞争前三名，只能将25匹马随机进行分组比赛，然后按照这些马的快慢情况进行排序，同一个字母代表是同一组的马，对应的下标代表他们在该组的排名，下图是我们在比赛5次之后给25匹马做的一个排序

 

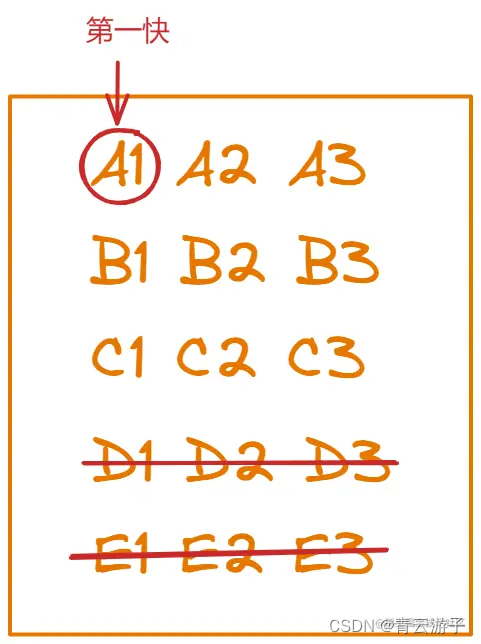
按照题目的要求呢，我们只需要找出最快的三匹马就行了，所以在下一次比赛之前，我们可以先把肯定不会被选上的马淘汰掉，因为我们已经知道每组内5匹马的快慢了，现在只有三个名额，跑的最慢的两匹马肯定是可以淘汰掉了，这样一来，我们现在要考虑的范围就是每一组前三快的马，如下图所示

注意：不同组的马我们现在还不知道谁快谁慢，比如A1和B1

 

2.将每组跑的最快的一匹马进行1次比赛，这样我们就可以选出25匹马中跑的第一快的马。

我们现在只知道相同组马的快慢，但是还不知道不同组马之间的快慢关系，所以这一次比赛就是为了在不同组中间挑选出最快的马，还有个目的就是要得到参与比赛中马的排名，这对我们后面缩小比赛范围提供很大的帮助

 

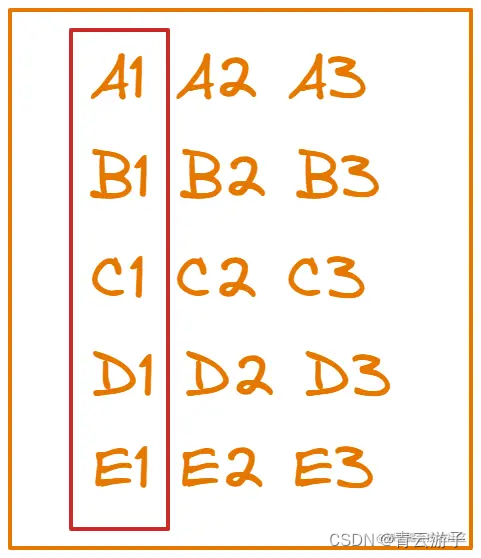
3.虽然现在我们只选好了第一快的马，但是淘汰掉那些没有机会的马后，我们发现最后可能进入前三的马只有5只了，刚好可以用1次比赛找到它们之间的快慢关系，这样在这5匹马中排名第一第二的马恰好就是25匹马中第二第三的马

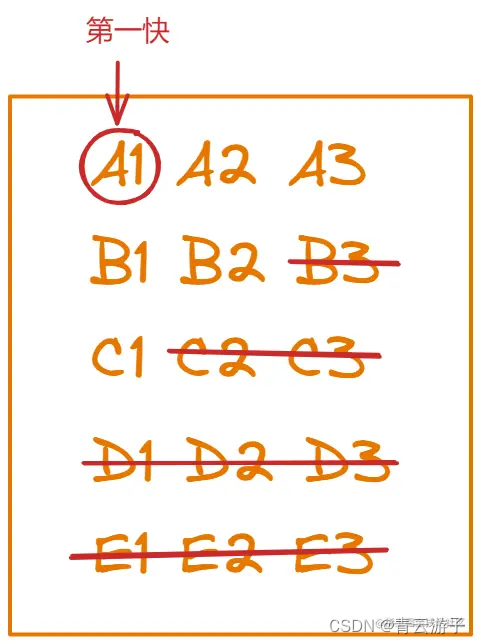
在A1-E1的比赛当中，我们已经选出了最快的马，这里我们认为A1最快就行，因为无论是哪匹马都不会影响最终的结果，他们的快慢关系姑且认为从快到慢就是A1-E1。我们现在还差第二快和第三快的马没有找出，也就是还有两个名额，那么B1和C1作为上次比赛的二三名还是有机会去争夺25匹马中的第二第三名的，但是D1和E1完全就没有机会了，因为他们落后于B1和C1，于此同时，D1和E1又是它们自己组中跑的最快的马，所以这两组其实就可以完全淘汰掉了

但现在其实还是有需要淘汰的马。由于A2和A3并没有和其它组的马跑过，我们现在只知道A2比A1慢，A3比A2慢，那么A2是有机会竞争到第二快的，A3是有机会竞争到第三快的。B1、C1我们知道的关系就是B1比C1快，但并不知道他们与A2、A3的关系，所以B1是有机会竞争第二快的，C1是有机会竞争第三快的。B2也没有和其它的马比过，只知道它比B1慢，所以B2是可能竞争第三名的。这样一来要淘汰的马就很明确了，B2和C1只有竞争到第三名的机会，那跑的比他们慢的B3、C2和C3肯定是挤不进前三的，直接淘汰掉就行，所以最终我们有几率竞争前三名的马如下图所示

这样一来，将余下的5匹马比赛一次，排名第一的马恰好就是我们要找的第二快马，排名第二的马恰好就是我们要找的第三快马

结果上面的分析，我们发现这题有意思的地方就是，第一快的马是单独比赛一次选出来的，而第二快和第三快的马是在同一场比赛中选出来的，找出最少比赛次数的关键所在就是我们要根据实时的比赛结果淘汰掉不可能有排名的马，从而达到压缩马数量的目的，这样可以让比赛的次数少很多

在网上发现了一种很有意思的解法，可以把最少的次数压缩到第六次，但是不知道符不符合题意：

首先前5轮还是要比的，任选一组的第3名和其他组的第一名进行比赛，如果这组的第三名恰好是这次比赛的第一名，那就意味着这一组对应的前三名就是25匹马中的前三名，这种方法虽然是碰运气，但好像跟题目中的“至少”并不冲突，所以自我感觉面试的时候可以提一嘴。如果题目要求找前5名也是一样的道理。

参考

稀土掘金https://juejin.cn/post/7077545879384637447