汉诺塔(hanoi)
题面是在说,你可以用两只手作为临时存储来玩汉诺塔,当且仅当拿起一个圆盘时,操作次数\(+1\)。
我们不妨将盘子两两分组,组内盘子看作一个大盘子,拿起它的花费是\(+2\),然后根据\(n\)的奇偶性来讨论(\(f(i)\)表示\(i\)盘经典汉诺塔问题的答案):
- \(n\)是偶数:转化成了\(\frac{n}{2}\)盘经典汉诺塔问题,答案即为\(f(\frac{n}{2})\times 2\)。
- \(n\)是奇数:相当于\(\lfloor\frac{n}{2}\rfloor\)个大盘子和\(1\)个小盘子,所以最终花费还要额外减去小盘子的移动次数,不难发现\(n\)盘经典汉诺塔问题,最顶上的盘子移动次数是\(2^{n-1}\),故答案就是\(f(\lceil\frac{n}{2}\rceil)\times 2-2^{\lfloor\frac{n}{2}\rfloor}\)。
经典汉诺塔答案递推公式:\(f(i)=2\times f(i-1)+1\)。递推需要用矩阵加速(或者利用等比数列也可以)。
矩阵加速写法的时间复杂度是\(O(2^3\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mod 998244353
using namespace std;
int n,base[2][2]{2,0,1,1},a[2][2],tmp[2][2];
void multi(int ans[2][2],int a[2][2],int b[2][2]){ans[0][0]=(a[0][0]*b[0][0]+a[0][1]*b[1][0])%mod;ans[0][1]=(a[0][0]*b[0][1]+a[0][1]*b[1][1])%mod;ans[1][0]=(a[1][0]*b[0][0]+a[1][1]*b[1][0])%mod;ans[1][1]=(a[1][0]*b[0][1]+a[1][1]*b[1][1])%mod;
}
void qpow(int b){while(b){if(b&1) multi(a,a,base);tmp[0][0]=base[0][0],tmp[0][1]=base[0][1],tmp[1][0]=base[1][0],tmp[1][1]=base[1][1];multi(base,tmp,tmp),b>>=1;}
}
int qpow(int a,int b){int ans=1;while(b){if(b&1) ans=ans*a%mod;a=a*a%mod,b>>=1;}return ans;
}
int f(int x){a[0][0]=0,a[0][1]=1;qpow(x);return a[0][0];
}
signed main(){cin>>n;if(n&1) cout<<(f(n/2+1)*2-qpow(2,n/2)+mod)%mod;else cout<<f(n/2)*2%mod;return 0;
}
与之国(and)
原题:P7970 [KSN2021] Binary Sea。
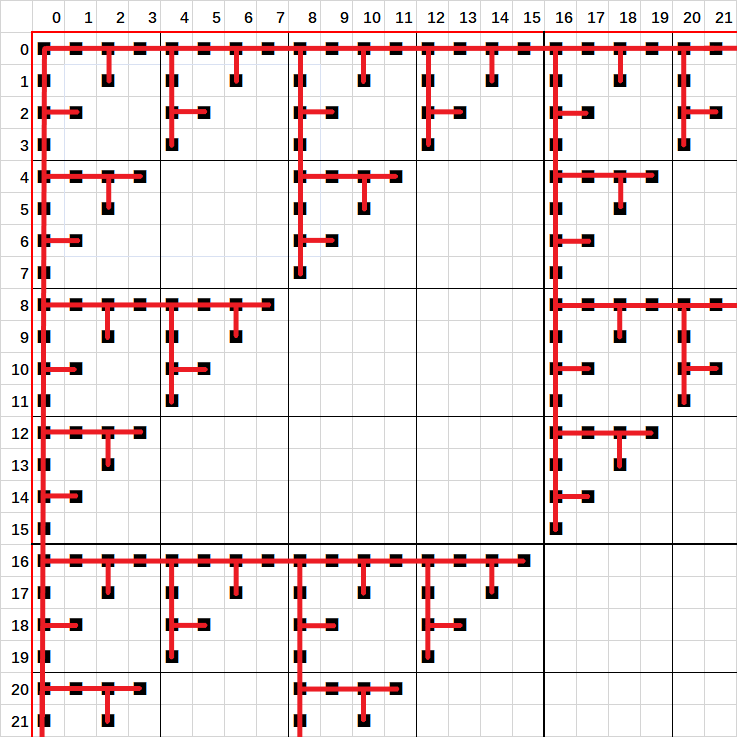
一开始的想法是将给定矩形剖成若干个小长方形,具体来说如下图。
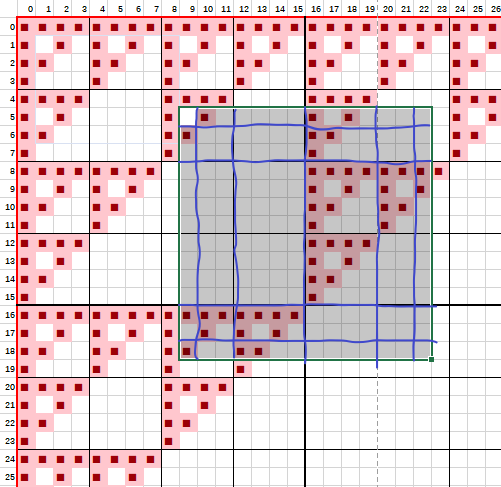
首先按照“对齐最近的\(2\)的整数次幂行&列”,对行和列进行分割,如蓝线所示,其实就和树状数组一样,每次\(x\leftarrow (x+\text{lowbit}(x))\)。这样我们分割出来的每个矩形都可以正好被剖成若干大小相同的正方形,且每个正方形都是对齐到它的尺寸的。
之所以这么思考是因为我一直以为每个矩形都是一个连通块,这样剖分后就容易考虑了,只需要判断右上角和左下角是不是陆地,即可判定它是否和右边、下边连通了。
如果这种方法可行,时间复杂度将是每个询问\(O(n\log^2 n)\),因为剖分成的行数和列数都是\(O(\log n)\)的。这样算来其实和暴力差不了多少了(
最关键的是上面那个结论不对,这个看图就能看出来,所以说做法假掉了。不过还是把代码放上来吧,位运算那块写的感觉还不错。
点击查看假掉的代码
#include<bits/stdc++.h>
using namespace std;
int n,ax,ay,bx,by;
int Px[80],Py[80],idxx,idxy;
bool bot[80][80],rig[80][80],vis[80][80];
inline int lowbit(int x){return x&-x;}
void dfs(int x,int y){if(x>idxx||y>idxy||vis[x][y]) return;vis[x][y]=1;if(bot[x][y]) dfs(x+1,y);if(rig[x][y]) dfs(x,y+1);
}
signed main(){cin>>n;while(n--){cin>>ax>>ay>>bx>>by;int tax=ax,tay=ay;idxx=idxy=0;if(tax) while(tax+lowbit(tax)<=bx+1) Px[++idxx]=lowbit(tax),tax+=lowbit(tax);if(tay) while(tay+lowbit(tay)<=by+1) Py[++idxy]=lowbit(tay),tay+=lowbit(tay);for(int i=29;~i;i--) if(tax+(1<<i)<=bx+1) tax+=(1<<i),Px[++idxx]=(1<<i);for(int i=29;~i;i--) if(tay+(1<<i)<=by+1) tay+=(1<<i),Py[++idxy]=(1<<i);Px[0]=ax,Py[0]=ay;for(int i=1;i<=idxx;i++) Px[i]+=Px[i-1];for(int i=1;i<=idxy;i++) Py[i]+=Py[i-1];for(int i=1;i<=idxx;i++){for(int j=1;j<=idxy;j++){if(!(Px[i-1]&(Py[j]-1))) rig[i][j]=1;if(!((Px[i]-1)&Py[j-1])) bot[i][j]=1;}}int cnt=0;for(int i=1;i<=idxx;i++){for(int j=1;j<=idxy;j++){if((rig[i][j]||bot[i][j])&&!vis[i][j]) dfs(i,j),cnt++;}}cout<<cnt<<"\n";}return 0;
}
这道题的正解,需要从另一个角度思考。
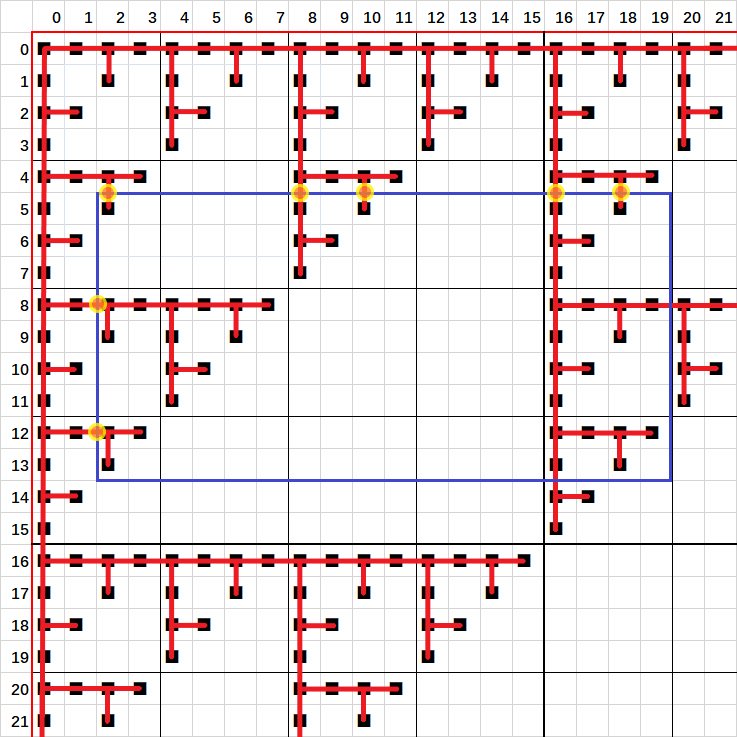
如图,如果把节点和自己右边和下边的节点(如果有)进行连边操作,整个图就是一棵二叉树。我们不难发现,每次询问的答案就是矩形左边缘和上边缘上边的条数之和。
拿上边缘\(top\)举例(左边缘同理),答案就是:
用前缀和的思想转化成两个\(\sum\)相减,然后用数位dp求解就好了~
顺带为自己之前写的数位dp随笔打个广告:上篇、下篇
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,ax,ay,bx,by,f[30],A,B;//A为限制,B为要参与求解的数
int dfs(int pos,bool limit){//pos从30到1 if(!pos) return 1;if(!limit&&f[pos]) return f[pos];int rig=limit?((A>>(pos-1))&1):1,ans=0;for(int i=0;i<=rig;i++){if((B>>(pos-1))&i&1) continue;ans+=dfs(pos-1,limit&&i==rig);}if(!limit) f[pos]=ans;return ans;
}
int solve(int x,int l,int r){memset(f,0,sizeof f);int ans1,ans2;B=x,A=r,ans1=dfs(30,1);A=l-1,ans2=l?dfs(30,1):0;return ans1-ans2;
}
signed main(){ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr);cin>>n;while(n--){cin>>ax>>ay>>bx>>by;if(!ax&&!ay) cout<<"1\n";else cout<<(bool)ax*solve(ax|(ax-1),ay,by)+(bool)ay*solve(ay|(ay-1),ax,bx)<<"\n";}return 0;
}



.assets/image-20241115003008761.png)