有理逼近AAA算法

用于有理逼近的AAA算法

The AAA Algorithm for Rational Approximation, Yuji Nakatsukasa, Olivier Sète, and Lloyd N. Trefethen, SIAM Journal on Scientific Computing 2018 40:3, A1494-A1522, https://doi.org/10.1137/16M1106122

一、算法用途

AAA算法是有理逼近算法，同其他逼近算法一样，是利用某复函数的函数点值对来“插值”出一个有理式的近似值。常见的逼近算法有：拉格朗日插值逼近，三角插值逼近(傅里叶级数)，切比雪夫多项式逼近等等。

AAA算法的全称是 adaptive Antoulas-Anderson 。主要解决了有理逼近时出现的伪极点 (spurious poles) 现象。

伪极点

伪极点是指在数值计算和逼近中出现的非物理性极点。它们通常出现在用有理函数逼近一个目标函数的过程中，尤其在使用某些加速收敛算法或有理逼近方法时（例如Padé逼近），这些伪极点往往不是原始函数固有的特征，而是数值方法带来的虚假结果。

例如非常常见的龙格现象，使用拉格朗日多项式逼近如下函数：

\[f(z)=\frac{1}{1+25z^2} \]

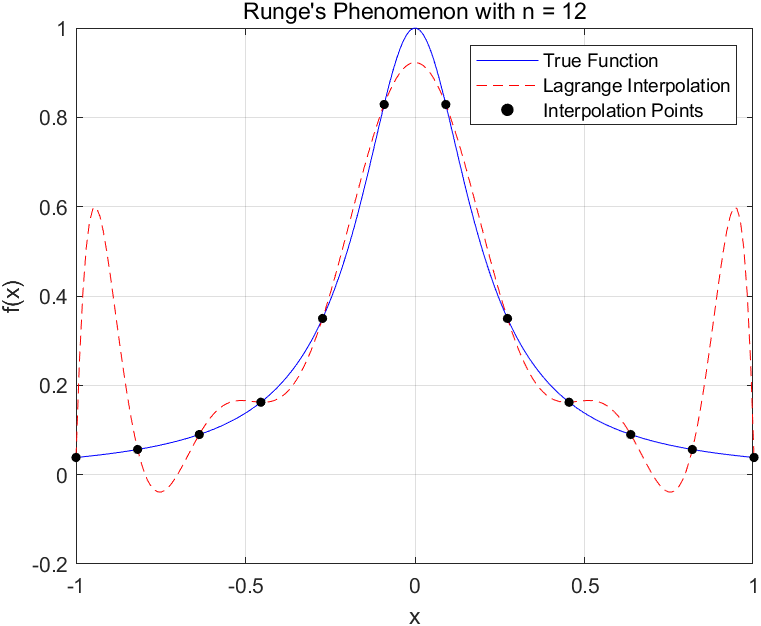
虚线所对应的就是一个有理逼近式，而在两边出现了伪极点。在复逼近时，除了伪极点外，还有Froissart doublets现象，即极点和零点非常接近。

二、算法流程

质心形式的拉格朗日插值

定义插值集合为 \(\{(z_j, f_j)\}_{j=1}^M\)，其中 \(M \gg 1\) 为数据量。

使用质心形式的拉格朗日插值：

\[r(z)= \sum_{j=1}^m \frac{w_j f_j}{z - z_j} \bigg/ \sum_{j=1}^{m} \frac{w_j}{z-z_j} = \frac{n(z)}{d(z)} \]

其中 \(w_j\) 是权重，\(m\) 是已经被选择了的插值支撑点。权重将求解一个最小二乘问题得到。

如上只是质心形式的拉格朗日插值的基本过程。如果想达到更大精度，插值算法将再选择一个插值节点，然后重新计算权重。对于初始的质心拉格朗日插值来说，新插值节点的选择是随机的（任意的），AAA算法则是基于一个贪婪准则来选择的。

权重计算和新节点的选择

权重的计算需要求解如下的问题：

\[\min\ \|fd-n\|_{Z^{(m)}}, \ \|w\|_m = 1 \]

新节点将从 \(Z^{(m)}=Z \textbackslash \{z_1, \cdots, z_m\}\) 中选择当前有理逼近 \(r(z)\) 和 \(f(z)\) 残差最大的点，这样才能满足上述的 \(\min\) 取到。换言之总选择目前拟合结果最差的点进入支撑集。

消除可能的伪极点

消除伪极点需要额外求解一个最小二乘问题。计算所有支撑点的留数。选择留数最小的支撑点，去除出支撑集，再重新计算权重。

伪代码流程

initial all parameters
while(step < max):compute the all distance of Zmselect the largest distance zm as new support pointsolve the weight vector w with min problemcompute all residues of zm
if there are Froissart doublets:select the minus of residues and delete from the support setrecompute the weight vector w

三、算法结果

利用单位圆上的100个均匀点逼近如下函数：

\[f(z) = \frac{\tan z}{1 - 16 z^4} \]

如上函数极点为：

\[z_1 = \frac{1}{2} \exp\left( \frac{k}{2}\pi i \right),\ k \in \Z \\ z_2 = \frac{\pi}{2} + k\pi, \ k \in \Z \]

在不启用最后一个去除双峰极点的算法下，获得逼近函数 \(r(z)\) 的极点如下：

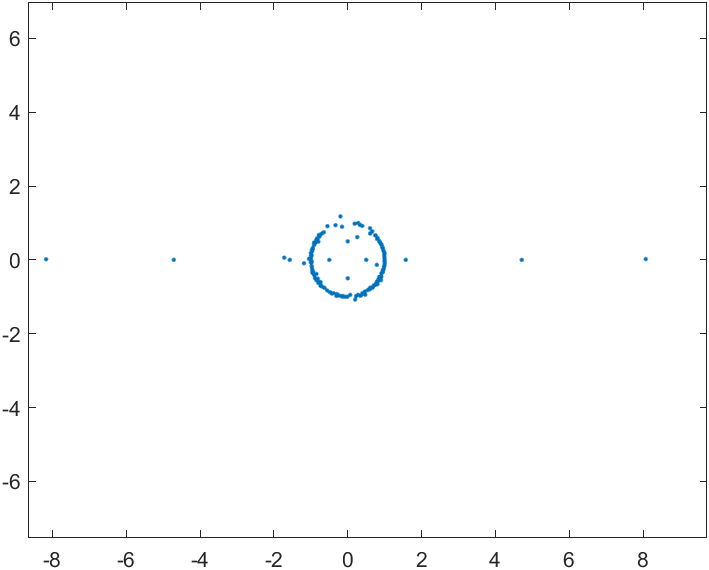
可以发现除了真正的 \(f(z)\) 的极点外，单位圆附近还有许多伪极点。

启用去除伪极点的代码后，重绘 \(r(z)\) 的极点如下：

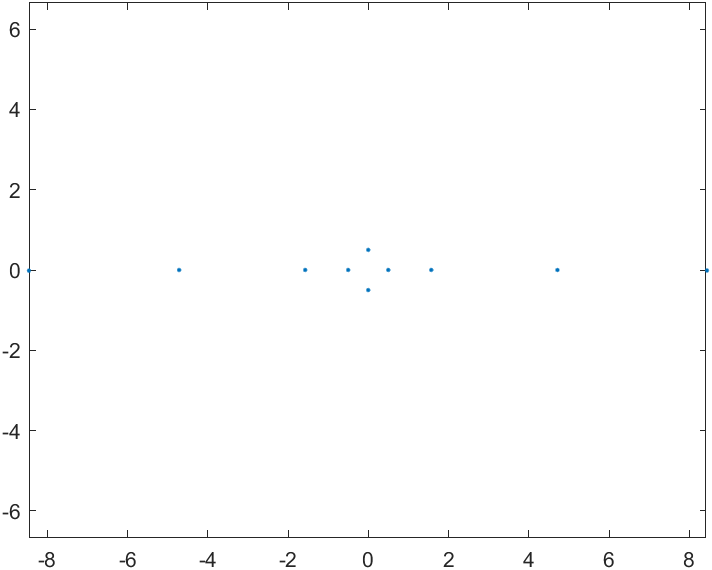
正常。不过，由于只用了单位圆上的数据，在较远处的极点原本应为 \(\pm 5\pi/2\)，外插误差较大。

四、代码

aaa.m

function [r,pol,res,zer,z,f,w,errvec] = aaa(F,Z,tol,mmax) 
% aaa rational approximation of data F on set Z 
%       [r,pol,res,zer,z,f,w,errvec] = aaa(F,Z,tol,mmax) 
%  
% Input:  F = vector of data values, or a function handle 
%         Z = vector of sample points 
%         tol = relative tolerance tol, set to 1e-13 if omitted 
%         mmax: max type is (mmax-1,mmax-1), set to 100 if omitted 
%  
% Output: r = AAA approximant to F (function handle) 
%         pol,res,zer = vectors of poles, residues, zeros 
%         z,f,w = vectors of support pts, function values, weights 
%         errvec = vector of errors at each step
M = length(Z);                              % number of sample points 
if nargin<3, tol = 1e-13; end               % default relative tol 1e-13 
if nargin<4, mmax = 100; end                % default max type (99,99) 
if ~isfloat(F), F = F(Z); end               % convert function handle to vector 
Z = Z(:); F = F(:);                         % work with column vectors 
SF = spdiags(F,0,M,M);                      % left scaling matrix 
J = 1:M; z = []; f = []; C = [];            % initializations 
errvec = []; R = mean(F);for m = 1:mmax                              % main loop [~,j] = max(abs(F-R));                  % select next support point z = [z; Z(j)]; f = [f; F(j)];           % update support points, data values J(J==j) = [];                           % update index vector C = [C 1./(Z-Z(j))];                    % next column of Cauchy matrix Sf = diag(f);                           % right scaling matrix A = SF*C - C*Sf;                        % Loewner matrix [~,~,V] = svd(A(J,:),0);                % SVD w = V(:,m);                             % weight vector = min sing vector N = C*(w.*f); D = C*w;                  % numerator and denominator R = F; R(J) = N(J)./D(J);               % rational approximation err = norm(F-R,inf); errvec = [errvec; err];                 % max error at sample points if err <= tol*norm(F,inf), break, end   % stop if converged 
end
r = @(zz) feval(@rhandle,zz,z,f,w);         % AAA approximant as function handle 
[pol,res,zer] = prz(r,z,f,w);               % poles, residues, and zeros 
[r,pol,res,zer,z,f,w] = ... cleanup(r,pol,res,zer,z,f,w,Z,F);       % remove Frois. doublets (optional)function [pol,res,zer] = prz(r,z,f,w)       % compute poles, residues, zeros 
m = length(w); B = eye(m+1); B(1,1) = 0; 
E = [0 w.'; ones(m,1) diag(z)]; 
pol = eig(E,B); pol = pol(~isinf(pol));     % poles 
dz = 1e-5 * exp(2i*pi*(1:4)/4);             
res = r(bsxfun(@plus,pol,dz))*dz.'/4;       % residues = r( pol + dz ) * dz / 4
E = [0 (w.*f).'; ones(m,1) diag(z)]; 
zer = eig(E,B); zer = zer(~isinf(zer));     % zerosfunction r = rhandle(zz,z,f,w)              % evaluate r at zz 
zv = zz(:);                                 % vectorize zz if necessary 
CC = 1./bsxfun(@minus,zv,z.');              % Cauchy matrix 
r = (CC*(w.*f))./(CC*w);                    % AAA approx as vector 
ii = find(isnan(r));                        % find values NaN = Inf/Inf if any 
for j = 1:length(ii) r(ii(j)) = f(find(zv(ii(j))==z));       % force interpolation there 
end 
r = reshape(r,size(zz));                    % AAA approxfunction [r,pol,res,zer,z,f,w] = cleanup(r,pol,res,zer,z,f,w,Z,F) 
m = length(z); 
M = length(Z); 
ii = find(abs(res)<1e-13);              % find negligible residues 
ni = length(ii); 
if ni == 0, return, end 
fprintf('%d Froissart doublets\n',ni)for j = 1:ni azp = abs(z-pol(ii(j))); jj = find(azp == min(azp),1); z(jj) = []; f(jj) = [];             % remove nearest support points 
endfor j = 1:length(z) F(Z==z(j)) = []; Z(Z==z(j)) = []; 
endm = m-length(ii); 
SF = spdiags(F,0,M-m,M-m); 
Sf = diag(f); 
C = 1./bsxfun(@minus,Z,z.'); 
A = SF*C - C*Sf; 
[~,~,V] = svd(A,0); 
w = V(:,m);                             % solve least-squares problem again 
r = @(zz) feval(@rhandle,zz,z,f,w); 
[pol,res,zer] = prz(r,z,f,w);           % poles, residues, and zeros

runge.m

% Runge's Phenomenon
f = @(x) 1 ./ (1 + 25 * x.^2);n = 12; 
x_interp = linspace(-1, 1, n);x_plot = linspace(-1, 1, 200);
y_plot = f(x_plot);y_interp = zeros(size(x_plot));
for i = 1:nL = ones(size(x_plot)); % Lagrange basis polynomialsfor j = [1:i-1, i+1:n]L = L .* (x_plot - x_interp(j)) / (x_interp(i) - x_interp(j));endy_interp = y_interp + f(x_interp(i)) * L; % f(x_interp) is y_0
end% Plot the true function and the interpolation polynomial
figure;
plot(x_plot, y_plot, 'b'); % Plot true function
hold on;
plot(x_plot, y_interp, 'r--'); % Plot interpolated polynomial
scatter(x_interp, f(x_interp), 20, 'filled', 'k'); % Show interpolation points
legend('True Function', 'Lagrange Interpolation', 'Interpolation Points');
title(['Runge''s Phenomenon with n = ', num2str(n)]);
xlabel('x');
ylabel('f(x)');
grid on;
hold off;

main.m

Z = exp(1i * linspace(0, 2*pi, 1000)); % unityF = @(z) tan(z) ./ (1 - 16 * z.^4);plot(F(Z))
axis('equal')[r,pol,res,zer,z,f,w,errvec] = aaa(F, Z);plot(pol, '.')
axis('equal')