Codeforces Round 985 div2 个人题解(A~E)

news/2024/11/16 1:13:32/文章来源:https://www.cnblogs.com/extractstars/p/18548943

Codeforces Round 985 div2 个人题解(A~E)

Dashboard - Codeforces Round 987 (Div. 2) - Codeforces

火车头

#include <bits/stdc++.h>using namespace std;#define ft first
#define sd second#define yes cout << "yes\n"
#define no cout << "no\n"#define Yes cout << "Yes\n"
#define No cout << "No\n"#define YES cout << "YES\n"
#define NO cout << "NO\n"#define pb push_back
#define eb emplace_back#define all(x) x.begin(), x.end()
#define all1(x) x.begin() + 1, x.end()
#define unq_all(x) x.erase(unique(all(x)), x.end())
#define unq_all1(x) x.erase(unique(all1(x)), x.end())
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3fLL#define RED cout << "\033[91m"     // 红色
#define GREEN cout << "\033[92m"   // 绿色
#define YELLOW cout << "\033[93m"  // 蓝色
#define BLUE cout << "\033[94m"    // 品红
#define MAGENTA cout << "\033[95m" // 青色
#define CYAN cout << "\033[96m"    // 青色
#define RESET cout << "\033[0m"    // 重置typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
// typedef __int128_t i128;typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ll, int> pli;
typedef pair<string, ll> psl;typedef tuple<int, int, int> ti3;
typedef tuple<ll, ll, ll> tl3;
typedef tuple<ld, ld, ld> tld3;typedef vector<bool> vb;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef vector<string> vs;
typedef vector<vi> vvi;
typedef vector<vl> vvl;// std::mt19937_64 rng(std::chrono::steady_clock::now().time_since_epoch().count());template <typename T>
inline T read()
{T x = 0;int y = 1;char ch = getchar();while (ch > '9' || ch < '0'){if (ch == '-')y = -1;ch = getchar();}while (ch >= '0' && ch <= '9'){x = (x << 3) + (x << 1) + (ch ^ 48);ch = getchar();}return x * y;
}template <typename T>
inline void write(T x)
{if (x < 0){putchar('-');x = -x;}if (x >= 10){write(x / 10);}putchar(x % 10 + '0');
}/*#####################################BEGIN#####################################*/
void solve()
{
}int main()
{ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);// freopen("test.in", "r", stdin);// freopen("test.out", "w", stdout);int _ = 1;std::cin >> _;while (_--){solve();}return 0;
}/*######################################END######################################*/
// 链接：

A. Penchick and Modern Monument

在繁华大都市马尼拉的摩天大楼中，菲律宾最新的 Noiph 购物中心刚刚竣工！建筑经理潘奇克下令用 $n$ 根柱子建造一座最先进的纪念碑。

纪念碑支柱的高度可以表示为由 $n$ 个正整数组成的数组 $h$，其中 $h_i$ 表示 $1$ 和 $n$ 之间所有 $i$ 根支柱的高度。

彭契克希望柱子的高度按不递减的顺序排列，即 $h_i \leq h_{i+1}$，对于所有 $i$ 在 $1$ 和 $n-1$ 之间。然而，由于混淆，纪念碑的柱子高度是按不递增的顺序排列的，即 $h_i \geq h_{i+1}$，对于所有 $i$ 在 $1$ 和 $n-1$ 之间。

幸运的是，彭奇克可以修改石碑，并根据需要对石柱进行以下操作：

将石柱的高度修改为任意正整数。形式上，选择一个索引 $1 \leq i \leq n$ 和一个正整数 $x$。然后赋值 $h_i := x$。帮助潘奇克确定最少需要多少次运算才能使纪念碑支柱的高度不递减。

输入
每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ $(1 \leq t \leq 1000)$。测试用例说明如下。

每个测试用例的第一行都包含一个整数 $n$ $(1 \leq n \leq 50)$ — 柱子数量。

每个测试用例的第二行包含 $n$ 个整数 $h_1, h_2, \ldots, h_n$ $(1 \leq h_i \leq n$ 且 $h_i \geq h_{i+1})$ — 支柱的高度。

请注意，给定数组 $h$ 是非递增数组。

输出
对于每个测试用例，输出一个整数，表示使支柱高度不递减所需的最小操作数。

示例
输入

输出

4
1
0

提示
在第一个测试用例中，柱子的初始高度是 $h=[5, 4, 3, 2, 1]$。

在第一次操作中，潘奇克将柱子 $1$ 的高度改为 $h_1 := 2$。
在第二次操作中，他将柱子 $2$ 的高度改为 $h_2 := 2$。
在第三次操作中，他将柱子 $4$ 的高度改为 $h_4 := 4$。
在第四次操作中，他将柱子 $5$ 的高度改为 $h_5 := 4$。
经过这些操作后，柱子的高度为 $h=[2, 2, 3, 4, 4]$，这符合不递减的要求。可以证明，彭奇克在少于 $4$ 次操作内无法使柱子的高度不递减。

在第二个测试用例中，彭奇克可以通过将柱子 $3$ 的高度改为 $h_3 := 2$ 来使柱子的高度不递减。

在第三个测试用例中，柱子的高度已经是非递减的，因此不需要任何操作。

解题思路

由于数组是不递增给出，因此我们最多保留一种原数组的数字，所以找出最多数量的数字进行保留即可。

代码实现

void solve()
{int n;cin >> n;map<int, int> mp;int mx = 0;for (int i = 0; i < n; i++){int x;cin >> x;mp[x]++;mx = max(mx, mp[x]);}cout << n - mx << "\n";
}

B. Penchick and Satay Sticks

Penchick 和他的朋友 Kohane 正在印度尼西亚游览，他们的下一站是泗水！

在泗水熙熙攘攘的小吃摊上，Kohane 买了 $n$ 根沙爹，并把它们排成一排，其中第 $i$ 根沙爹的长度为 $p_i$。已知 $p$ 是长度为 $n$ 的排列组合。

彭奇克想把沙爹棒按长度递增的顺序排列，这样每个 $1 \leq i \leq n$ 都有 $p_i = i$。为了好玩，他们制定了一条规则：他们只能交换长度相差 $1$ 的相邻沙爹棒。从形式上看，他们可以执行以下任意次数（包括零次）的操作：

选择一个索引 $i$ $(1 \leq i \leq n-1)$，使得 $|p_{i+1} - p_i| = 1$；
交换 $p_i$ 和 $p_{i+1}$。
判断是否可以通过上述操作对排列 $p$ 进行排序，从而对沙爹棒进行排序。

输入
每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ $(1 \leq t \leq 2 \cdot 10^5)$。测试用例说明如下。

每个测试用例的第一行都包含一个整数 $n$ $(1 \leq n \leq 2 \cdot 10^5)$ — 沙爹棒的数量。

每个测试用例的第二行包含 $n$ 个整数 $p_1, p_2, \ldots, p_n$ $(1 \leq p_i \leq n)$ — 表示沙爹棒长度的排列 $p$。

保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。

输出
对于每个测试用例，如果可以通过执行操作对排列 $p$ 进行排序，则输出 "YES"。否则，输出 "NO"。

可以用任何大小写（大写或小写）输出答案。例如，字符串 "yEs"、"yes"、"Yes" 和 "YES" 将被视为肯定回答。

示例
输入

输出

YES
NO

提示
在第一个测试用例中，我们可以通过在索引 $1$ 执行操作对排列 $p=[2,1,3,4]$ 进行排序（$|p_2 - p_1| = |1 - 2| = 1$），结果为 $p=[1,2,3,4]$。

在第二个测试用例中，可以证明无法通过执行操作对排列 $p=[4,2,3,1]$ 进行排序。以下是可以对该排列执行的一系列操作示例：

选择 $i=2$（$|p_3 - p_2| = |3 - 2| = 1$）。结果为 $p=[4,3,2,1]$。
选择 $i=1$（$|p_2 - p_1| = |3 - 4| = 1$）。结果为 $p=[3,4,2,1]$。
选择 $i=3$（$|p_4 - p_3| = |1 - 2| = 1$）。结果为 $p=[3,4,1,2]$。
不幸的是，经过这些操作后，排列 $p$ 仍然未排序。

解题思路

观察发现，如果一个数距离它的原位置大于 $1$ ,即 $|p_i-i| \gt 1$ 则一定无法交换到符合条件

代码实现

void solve()
{int n;cin >> n;int mx = 0;for (int i = 1; i <= n; i++){int x;cin >> x;mx = max(mx, abs(x - i));}if (mx > 1)NO;elseYES;
}

C. Penchick and BBQ Buns

Penchick 喜欢两样东西：方块数字和港式烧腊包！在他生日的时候，Kohane 想送他一份礼物：$n$ 个从左到右排列的烧腊包。烧腊包的馅料有 $10^6$ 种，编号从 $1$ 到 $10^6$。为了确保彭奇克会喜欢这份礼物，Kohane 有几个目标：

每种馅料都不能使用一次；也就是说，每种馅料要么完全不出现，要么至少出现两次。
任何两个包子 $i$ 和 $j$ 的馅料相同，它们之间的距离 $|i−j|$ 必须是一个完美的正方形。

请帮助 Kohane 找到选择包子馅的有效方法，或确定是否不可能满足她的目标！

输入
每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ $(1 \leq t \leq 2 \cdot 10^5)$。测试用例说明如下。

每个测试用例的唯一一行包含一个整数 $n$ $(1 \leq n \leq 2 \cdot 10^5)$ — 烧烤包的数量。

保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

输出
对于每个测试案例，如果没有有效的馅料选择，则输出 $-1$。否则，输出 $n$ 个整数，其中第 $i$ 个整数代表第 $i$ 个烧烤包的馅料。如果有多个解，打印任意一个解。

示例
输入

2
3
12

输出

-1
1 2 3 6 10 2 7 6 10 1 7 3

提示
在第一个测试用例中，选择的馅料 "1 1 1" 是不允许的，因为包子 $1$ 和 $3$ 的馅料相同，但它们之间的距离是 $2$，这不是一个完美的平方。选择的馅料 "1 1 2" 也不允许，因为馅料 $2$ 只使用了一次。

在第二个测试用例中，解决方案是有效的，因为没有馅料只使用了一次，且任何两个相同馅料的包子之间的距离都是一个完美的平方。例如，包子 $1$ 和 $10$ 都有馅料 $1$，它们之间的距离为 $9=3^2$。类似地，包子 $5$ 和 $9$ 都有馅料 $10$，它们之间的距离为 $4=2^2$。

解题思路

对于 $n$ 为偶数，我们不难发现，我们只需要形如 "1 1 2 2 3 3 4 4 5 5 ..." 的样子进行构造即可。

对于 $n$ 为奇数，我们一定需要有一种馅料需要放在至少三个位置。

设这三个位置为 $i,j,k ,i \lt j \lt k$ 则 $(j-i)+(k-j)=(k-i)$ 。由于 $(j-i),(k-j),(k-i)$ 都为完全平方数，我们不难想到勾股定理。最小的勾股数为 $9,16,25 $ 带入可得 $j-i=9,k-j=16,k-i=25$ 将 $k$ 设为符合条件的最小奇数 $27$ 即得 $i=2,j=11,k=27$。

易构造出长度为27的数组如下

2, 1, 3, 3, 2, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 1, 10, 10, 11, 11, 12, 12, 13, 13, 1

因此，我们只需要在 $n$ 为奇数时在最前面填充以上数组，剩余的按偶数情况处理即可。

代码实现

void solve()
{int n;cin >> n;int now = 1;vi v = {2, 1, 3, 3, 2, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 1, 10, 10, 11, 11, 12, 12, 13, 13, 1};bool flag = false;if (n & 1){if (n < 27){cout << "-1\n";return;}else{flag = true;now = 14;n -= 27;for (int i = 0; i < 27; i++){cout << v[i] << " ";}}}for (int i = 1; i <= n; i += 2){cout << now << " " << now++ << " ";}cout << "\n";
}

D. Penchick and Desert Rabbit

彭契克致力于挑战自己的极限，他挑战自己在阿拉伯沙漠的正午阳光下生存！

当彭奇克沿着一片线状绿洲跋涉时，发现一只沙漠兔正准备沿着一排棕榈树跳跃。这里有 $n$ 棵树，每棵树的高度用 $a_i$ 表示。

如果以下条件中有一个为真，兔子就可以从第 $i$ 棵树跳到第 $j$ 棵树：

$j < i$ 且 $a_j > a_i$
$j > i$ 且 $a_j < a_i$

对于从 $1$ 到 $n$ 的每棵树 $i$，确定兔子从第 $i$ 棵树开始所能到达的最大高度。

输入
第一行包含测试用例的数量 $t$ $(1 \leq t \leq 5 \cdot 10^5)$。测试用例说明如下。

每个测试用例的第一行包含一个整数 $n$ $(1 \leq n \leq 5 \cdot 10^5)$ — 树的数量。

每个测试用例的第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$ $(1 \leq a_i \leq n)$ — 树的高度。

保证所有测试用例中 $n$ 的总和不超过 $5 \cdot 10^5$。

输出
对于每个测试用例，输出 $n$ 个整数。第 $i$ 个整数应该包含兔子从第 $i$ 棵树开始能到达的所有树的最大高度。

示例
输入

5
4
2 3 1 4
5
5 4 3 2 1
4
2 1 1 3
4
1 1 3 1
8
2 4 1 6 3 8 5 7

输出

3 3 3 4 
5 5 5 5 5 
2 2 2 3 
1 1 3 3 
8 8 8 8 8 8 8 8

提示
在第一个测试用例中，树的初始高度为 $a=[2,3,1,4]$。

如果兔子从第一棵树开始，它可以跳到第三棵树，因为 $3 > 1$ 且 $1 < 2$。然后，兔子可以跳到第二棵树，因为 $2 < 3$ 且 $3 > 1$。可以证明兔子无法到达第四棵树；因此，兔子可以到达的树的最大高度为 $a_2=3$。

如果兔子从第四棵树开始，它不需要跳跃，因为它已经在最高的树上。

在第二个测试用例中，无论从哪棵树开始，兔子都可以跳到第一棵树。

在第五个测试用例中，如果兔子从第五棵树开始，它可以跳到第四棵树。然后兔子可以跳到第七棵树，最后到达第六棵树。因此，兔子可以到达的树的最大高度为 $8$。

解题思路

如果只考虑向前跳即 $i\gt j$ ，则答案为前缀最大值。

考虑向后跳，我们一定是跳到小于自己的最远的地方，然后再向前跳到前缀最大值，用数组数组为会后缀的前缀最大值即可。

代码实现

template <typename T>
struct Fenwick
{int n;       // 数组大小vector<T> a; // 存储树状数组的数组// 构造函数，初始化树状数组Fenwick(int n_ = 0){init(n_);}// 初始化树状数组void init(int n_){n = n_;               // 设置大小a.assign(n + 1, T{}); // 初始化数组，所有元素为0}// 在索引 x 上添加值 vvoid add(int x, const T &v){for (int i = x; i <= n; i += i & -i){                        // 从 x 开始更新a[i] = max(a[i], v); // 更新当前节点}}// 计算前缀和，从 0 到 xT query(int x){T ans{}; // 初始化结果为 0for (int i = x; i > 0; i -= i & -i){                         // 从 x 向上遍历ans = max(ans, a[i]); // 累加当前节点的值}return ans; // 返回前缀和}
};void solve()
{int n;cin >> n;vi a(n + 1);Fenwick<int> fen(n);vi pre(n + 1);for (int i = 1; i <= n; i++){cin >> a[i];pre[i] = max(pre[i - 1], a[i]);}vi ans(n + 1);for (int i = n; i >= 1; i--){ans[i] = max(pre[i], fen.query(pre[i] - 1));fen.add(a[i], ans[i]);}for (int i = 1; i <= n; i++){cout << ans[i] << " \n"[i == n];}
}

E. Penchick and Chloe's Trees

离 Penchick 和 Chloe 前往新加坡的时间只剩下几个小时了，他们迫不及待地想去看看新加坡植物园的参天大树！为了抑制激动的心情，Penchick 制作了一棵扎根树，让 Chloe 和他自己忙个不停。

彭奇克有一棵有根树，包含 $n$ 个顶点，编号从 $1$ 到 $n$，顶点 $1$ 是根，克洛伊可以选择一个非负整数 $d$ 来创建一棵深度为 $d$ 的完美二叉树。

由于彭契克和克洛伊是好朋友，克洛伊希望自己的树与彭契克的树同构。为了满足这个条件，克洛伊可以在自己的树上执行以下任意次数的操作：

选择边 $(u,v)$，其中 $u$ 是 $v$ 的父节点。删除顶点 $v$ 和所有连接到 $v$ 的边，然后将 $v$ 之前的所有子代直接连接到 $u$。具体来说，在 $v$ 为叶子的边 $(u,v)$ 上进行操作将删除顶点 $v$，而不会添加任何新的边。

由于构建完美二叉树非常耗时，克洛伊希望选择最小值 $d$，这样深度为 $d$ 的完美二叉树就可以通过上述操作与彭契克的树同构。

输入
每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ $(1 \leq t \leq 10^5)$。测试用例说明如下。

每个测试用例的第一行都包含一个整数 $n$ $(2 \leq n \leq 10^6)$ — Penchick 树的顶点数。

每个测试用例的第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$ $(1 \leq p_i \leq i-1)$ — 顶点 $i$ 的父节点。

保证所有测试用例中 $n$ 的总和不超过 $10^6$。

输出
对于每个测试用例，每行输出一个整数：克洛伊完美二叉树的最小深度。

示例
输入

5
6
1 2 2 1 1
15
1 1 2 2 3 3 4 4 5 5 6 6 7 7
5
1 2 2 2
7
1 1 2 1 1 2
10
1 1 1 2 2 2 4 3 3

输出

提示
对于第一个测试用例，创建一棵深度为 $2$ 的完美二叉树。

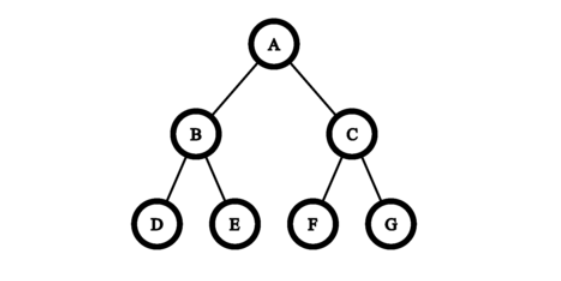
考虑在边 $AC$ 上执行操作。然后边 $AC$、$CF$ 和 $CG$ 被移除，并添加边 $AF$ 和 $AG$。

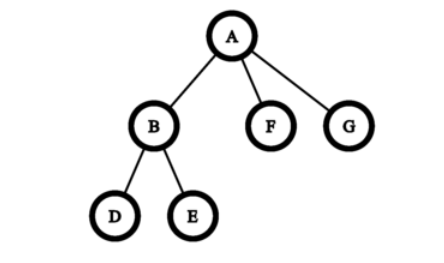
结果树与输入中给出的树同构。可以证明，在深度小于 $2$ 的二叉树上执行的操作序列无法导致与输入中给出的树同构的树。

在第二个测试用例中，树已经与深度为 $3$ 的完美二叉树同构。

解题思路

观察发现，对于一个节点，如果其子节点数量为 $2^n$ 个，我们至少需要向拓展 $n$ 层，然后删掉其它中间节点才能得到该节点。

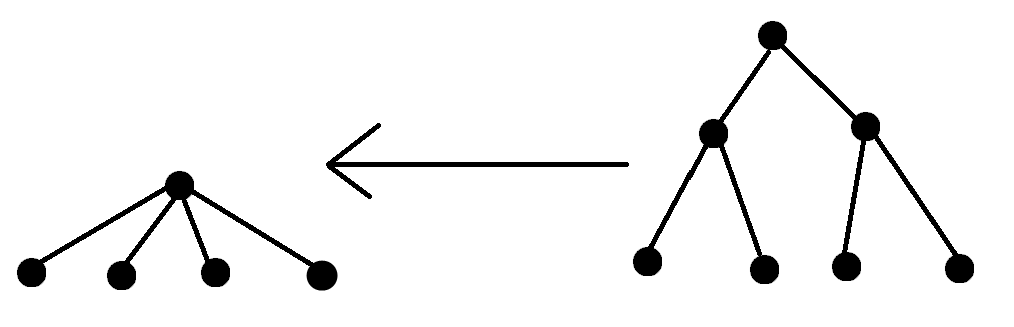
因此，我们可以很容易的推导出，如果一个节点的存在两个子节点需要层深相同，那么就可以将这两个子节点所需的层深合并然后加一。将所有子节点所需层深进行合并后，即可获得得到该节点所需的层深。

代码实现

void solve()
{int n;cin >> n;vector<vector<int>> adj(n + 1);for (int i = 2, x; i <= n; i++){cin >> x;adj[x].pb(i);}auto dfs = [&](auto &self, int u) -> int{set<int> st;if (adj[u].empty())return 0;for (int v : adj[u]){int d = self(self, v);while (st.count(d)){st.erase(d);d++;}st.insert(d);}int res = *(st.rbegin());// 对于链的情况要特判一下，防止忽略// 对于一个节点链接了多种不同深度的节点说明其至少还需要向下再走一层去提供其它节点if (st.size() >= 2 || adj[u].size() == 1)res++;return res;};cout << dfs(dfs, 1) << '\n';
}

这场开晚了，本来想着打小号的，结果开着大号看榜不小心交了一发，只能打大号了。再加上C题输错了，把$j-i=4$ 看成 $=4$ 直到赛后才发现问题出在哪里。人麻了，直接掉青了。不过也没关系，下场刚好div3，刚好可以上分。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/834363.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！