在数学和力学甚至机械专业中,质量-弹簧-阻尼系统是基础、经典的模型。其数学模型表示为:
$$
m\ddot{x} +c\dot{x} +kx = 0 \qquad(1)
$$
有限元模型比较简单,就是两个质量点+弹簧

假设上述式子的初值为
$$
\begin{cases}
u(0)=0.2
\
\dot{u}(0)=0
\end{cases}
$$
各项系数为
| 变量 | 数值 |
|---|---|
| m | 10 |
| k | 1000 |
| c | 20 |
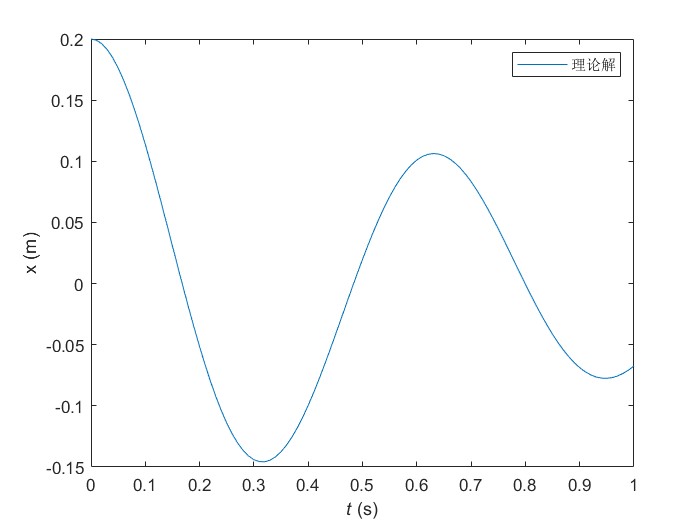
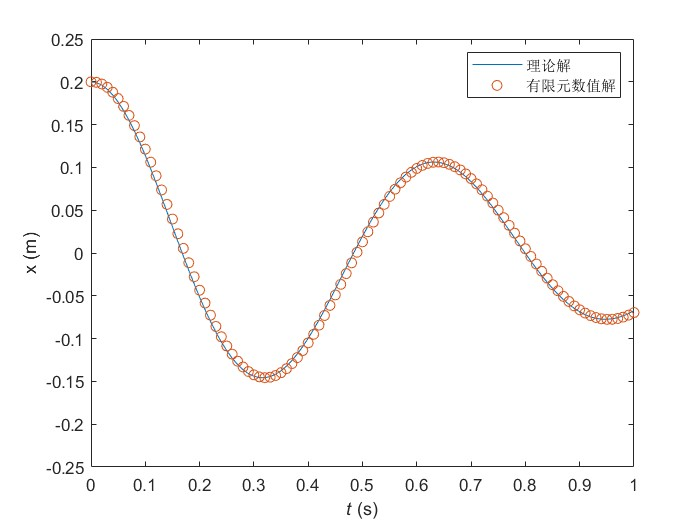
先通过MATLAB调用自带的ode45函数解一下上述这个式子,可以得到方程的理论解
MATLAB程序就贴在这里了
clear;
clc;
global k m c %方程的系数
%%
k=1000;
m=10;
c=20;%% 调用MATLAB自带函数ODE45求解方程,并将结果分别存放在t和y矩阵(向量)中
[t,y]=ode45(@test_theory,0:0.01:1,[0.2 0]);%% 画出质量点位移与时间的关系
plot(t,y(:,1))
hold on%% 设置坐标轴名以及图例
legend("理论解")
xlabel('{\itt} (s)');
ylabel('x (m)');%% 将二阶微分方程改成写一阶微分方程组
function dy=test_theory(~,y)
global k m c
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=-c/m*y(2)-k/m*y(1);
end
本案例不致力于记录如何解方程(1),此外,之前记录过如何关于如何解方程(1)。
其实,对于本案例中的微分方程,有限元也能给出相对精确的数值解,这一点是毋庸置疑的,因为我最近工作中要用到nastran这个有限元求解器,因此,就尝试了一下用nastran来求解上述微分方程。当然,用有限元软件进行求解的话,就得将上述方程“改写”成具体的模型。
这个模型在有限元软件中就是相对简单的模型了,即,两个点+一个弹簧,其中一个点模拟固定约束位置,另一个点则被赋予质量,弹簧则连接这两个点。那么方程中m和k的问题就轻松解决了。阻尼c该如何模拟呢?阻尼在现实的模型中也是肯定存在的,对于本案例的阻尼,是相对简单的,我们总是能在nastran中找到相应的参数,给参数赋予合适的数值,就能完美解决方程中阻尼的问题。
关于阻尼,我目前还是一知半解,对于复杂的装配体模型,不能十分“敏锐”地给出阻尼值,这块对我来说真的是十分困难,也是一直困扰我的存在,我承认这是我的短板,我还不能完全理解阻尼是如何对数值结果产生影响的。先在这里标记一下阻尼这个话题吧,希望以后看到阻尼相关的文章或者案例,能让我对“阻尼”再有清晰的认知吧。
回到这个案例,这里的阻尼就是比较直观的,是与速度相关的,对结果产生能量耗散的东西。先抛开阻尼系数的合理性,我们能看到,由于阻尼的存在,振幅在振动的过程中是越来越小的,说明系统的能量是耗散了的。
在频响分析中,阻尼是随频率有关的,在瞬态分析中,阻尼可能与速度相关,也可能与材料相关。nastran中根据不同的分析类型,可通过多种方式模拟阻尼。针对本案例(质量-弹簧-阻尼系统),模拟阻尼的手段有四种,可以是四种的结合,也可以单独设置进行模拟。先看一下阻尼的介绍:


$B$ 是阻尼矩阵,在patran中阻尼被四部分影响。
$B^1$ 是通过定义阻尼单元,直接定义结构的阻尼;
$B^2$ 目前不知道是什么含义,手册上解释说是B2PP直接输入的矩阵+传递函数。
$G$ 是整体结构阻尼系数;
$W_3$ 是圆频率(角频率)$\omega$,其中 $\omega = 2 \pi f$
$K$ 是整体刚度矩阵;
$W_4$ 将结构阻尼转换为等效粘性阻尼。
今天记录一下其中三种模拟阻尼的手段,第四种算是给自己挖的一个坑吧,日后有需要的话再填。
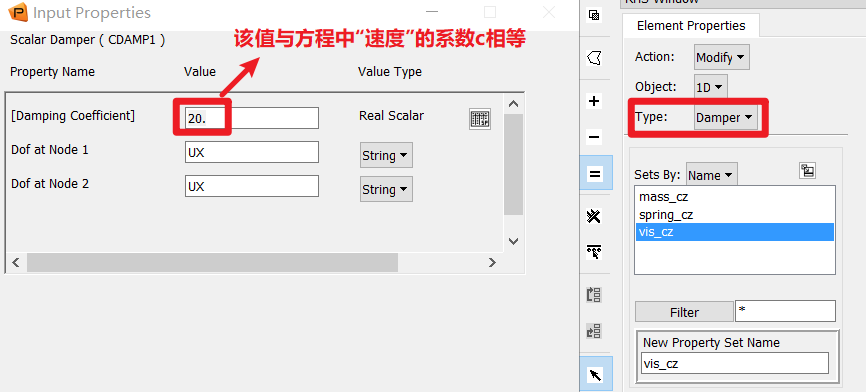
1.仅使用阻尼单元$B^1$
这种方式和弹簧类似,即两个质量点被弹簧和阻尼两个单元连接。
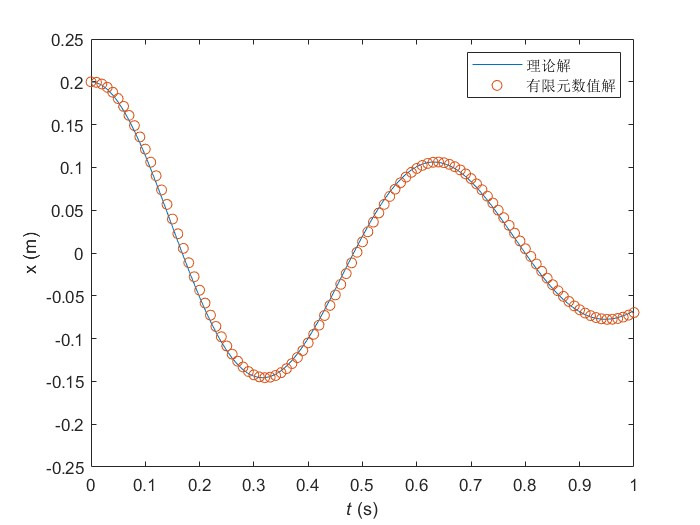
结果对比
2.仅使用整体结构阻尼&整体刚度&圆频率:$\frac{G}{W_3}[K] $
这里的$G$是整体阻尼系数,$W_3$是结构的圆频率$\omega$,$[K]$是结构的刚度,即1000。$G$、$W_3$、$\omega$与式(1)中的$c$的关系为:
$$
c=\frac{G}{W_3}[K]
$$
这种方法需要提前计算出圆频率
设置方法:
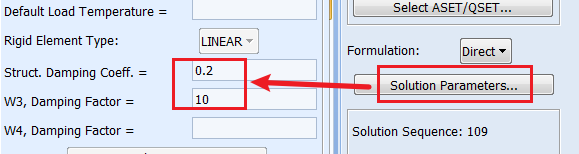
结果对比
3.仅使用单元刚度&单元阻尼&等效粘性阻尼:$\frac{1}{W_4} \sum G_E[K_E] $
本案例中的单元刚度矩阵$K_E$就是$K$,单元阻尼系数$G_E$就是弹簧单元的阻尼系数,$W_4$将结构阻尼转换为等效粘性阻尼。那么,阻尼就可以表示为:
$$
c=\frac{1}{W_4} \sum G_E[K_E]
$$
这种方法要设置单元阻尼:
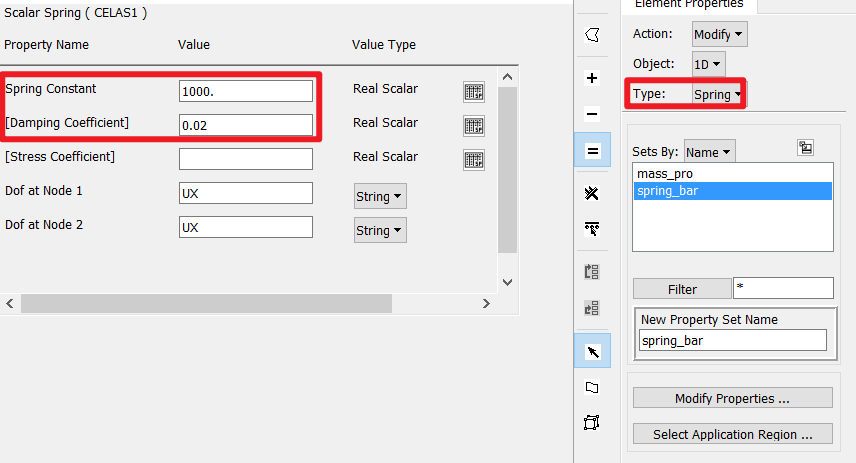
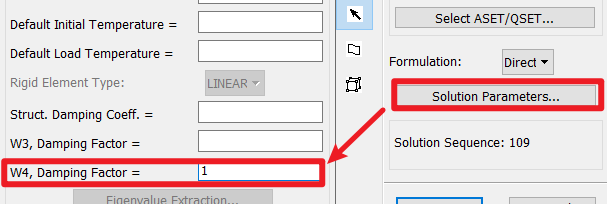
结果对比
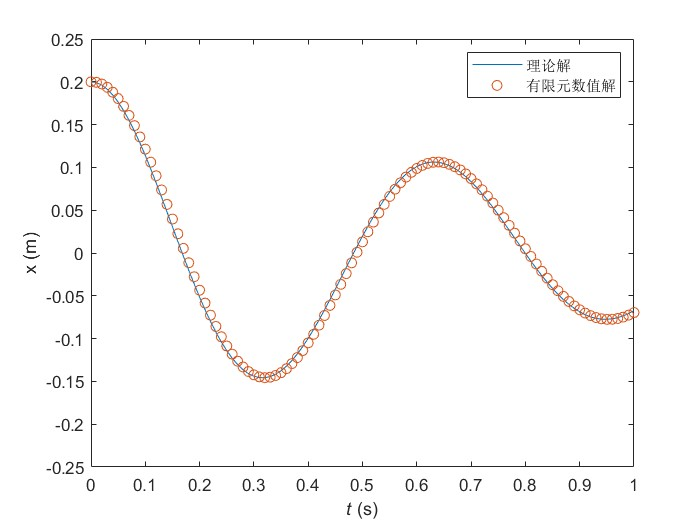
从对比结果上来看,这三种方式得到的结果都能和理论解完美吻合,这也能够满足我们的期望,挺好的,哈哈哈哈!
欢迎大家关注同名微信公众号:一页寄相思

三个案例的地址:
链接:https://pan.baidu.com/s/1OAxUiejGAmYlMdSDD5QQVA?pwd=sclh
提取码:sclh