组合数学基础 - 学习记录

news/2024/11/19 8:45:57/文章来源:https://www.cnblogs.com/lzl20220405/p/18554144

组合数学基础 - 学习笔记

代码集合

1. 加法 / 乘法原理

加法原理

指若有 $n$ 类选择完成工程，每类选择有 $a_i$ 个方法，总完成方法数为 $a_1+a_2+ \cdots +a_n$

乘法原理

指若有 $n$ 个步骤完成工程，每个步骤有 $a_i$ 种方法，总完成方法数为 $a_1 \times a_2 \times \cdots \times a_n$

P3197

正面不好想，从反面入手；每个房间的犯人有 $m$ 种选择，由乘法原理，总共有 $m^n$ 种情况；若每相邻两个房间犯人的信仰均不同，从前往后考虑，第一个房间有 $m$ 种选择，后面每个房间都需要与前一个房间不同，有 $m-1$ 种选择，因此共有 $m \times (m-1)^{n-1}$ 种情况

答案即为 $m^n-m \times (m-1)^{n-1}$，快速幂即可，实现时注意取模可能会出现负数

2. 排列组合

排列数

指从 $n$ 个元素中选 $m (m \le n)$ 个，按照一定顺序 排列的方法数，用符号 $A^{m}_{n}$ 表示

从 $n$ 个元素中选 $m$ 个按顺序排列，第 $1$ 个位置有 $n$ 种选择，第 $2$ 个位置有 $n-1$ 种选择 (不能选择第 $1$ 个位置上选过的)，……，第 $m$ 个位置上有 $n-m+1$ 个选择；因此，$A^{m}_{n} = n \times (n-1) \times \cdots \times (n-m+1)$

在原式上下同乘 $(n-m)!$ (! 表示阶乘)，就得到了 $A^{m}_n$ 的计算公式的另一表达形式

\[A^{m}_{n} = n \times (n-1) \times (n-2) \times \cdots \times (n-m+1) = \frac{n!}{(n-m)!} \]

组合数

组合数与排列数略有不同，仍然是从 $n$ 个元素中选 $m(m \le n)$ 个，区别在于它 不考虑顺序；组合数用符号 $C^{m}_{n}$ 或 $\dbinom{n}{m}$ 表示

设选出 $m$ 个元素，其不同顺序的排列 (就是 全排列 个数) 显然为 $m!$；因此重复的量为 $m!$，组合数的计算公式即为

\[C^{m}_{n} = \frac{A^{m}_{n}}{m!} = \frac{n!}{m!(n-m)!} \]

特别的，我们规定当 $m>n$ 时，$A^{m}_{n} = C^{m}_{n}=0$

组合数性质

\[C^{m}_{n} = C^{m}_{n-m}\tag1 \]

这是显然的，从 $n$ 个元素中挑 $m$ 个元素拿出来等价于从 $n$ 个元素中挑 $n-m$ 个元素放在原地

\[C^{m}_{n} = \frac{n!}{m!(n-m)!} = \frac{n}{m} \times \frac{(n-1)!}{(m-1)![(n-1)-(m-1)]!} = \frac{n}{m} \times C^{m-1}_{n-1}\tag2 \]

小组合数简单递推式

\[C^{m}_{n} = C^{m}_{n-1}+C^{m-1}_{n-1}\tag3 \]

组合数递推式，是 $(2)$ 的变式，证明如下

\[C^{m}_{n} = \frac{n}{m} \times C^{m-1}_{n-1} = (1 + \frac{n-m}{m}) \times C^{m-1}_{n-1} = \frac{n-m}{m} \times C^{m-1}_{n-1} + C^{m-1}_{n-1}\\ = \frac{n-m}{m} \times \frac{(n-1)!}{(m-1)!(n-m)!} + C^{m-1}_{n-1} = \frac{(n-1)!}{m!(n-m-1)!} + C^{m-1}_{n-1} = C^{m}_{n-1}+C^{m-1}_{n-1} \]

如何理解这个柿子？考虑其组合意义，选择 $n$ 中的一个元素为“特殊元素”；当选出的 $m$ 个元素包含特殊元素时，只需另外从非特殊的 $n-1$ 个元素中选 $m-1$ 个元素，方法数为 $C^{m-1}_{n-1}$；当选出的不包含特殊元素时，即从非特殊的 $n-1$ 个元素中选择 $m$ 个，方法数为 $C^{m}_{n-1}$

杨辉三角

杨辉三角是二项式系数在三角形上的几何体现 (二项式系数指 $(a+b)^n$ 各项的系数，二项式定理后面再讲)，同时也形象地表现出了组合数递推式

C(0,0)=1
C(0,1)=1 C(1,1)=1
C(0,2)=1 C(1,2)=2 C(2,2)=1
C(0,3)=1 C(1,3)=3 C(2,3)=3 C(3,3)=1
C(0,4)=1 C(1,4)=4 C(2,4)=6 C(3,4)=4 C(4,4)=1
……

我们发现第 $i$ 行 $j$ 列的数就是 第 $\bm{i-1}$ 行 $\bm{j-1}$ 列的数与第 $\bm{i-1}$ 行 $\bm{j}$ 列的数之和，这就是组合数递推式

P2822

如果我们在每一步都暴力阶乘求解组合数，时间开销无法接受；题目问的是从 $0$ 开始一个范围内所有的组合数，因此可以使用组合数递推式配合前缀和求出每一行所有满足要求的组合数的数量

注意需要取模，可以边求边模，模之后为 $0$ 则代表当前组合数符合要求，此时更新前缀和即可

Lucas 定理

Lucas 定理用于求解大组合数取模问题，模数 $p$ 必须为素数，定理内容如下 (证明略)

\[C^{m}_{n} \bmod p = C^{\lfloor m/p \rfloor}_{\lfloor n/p \rfloor} \times C^{m \bmod p}_{n \bmod p} \bmod p \]

使用定理后可以直接求解 $\displaystyle C^{m \bmod p}_{n \bmod p}$，对于 $C^{\lfloor m/p \rfloor}_{\lfloor n/p \rfloor}$ 可以继续递归求解

使用 Lucas 定理时，模数 $p$ 的范围不能太大，一般在 $1e5$ 左右；递归到 $m=0$ 时返回 $1$ 即可

P3807

卢卡斯定理模板题，直接套定理即可，需要用常见技巧 预处理阶乘，不然会 TLE

插板法

~~死去的小奥突然开始攻击我~~

插板法可以求解相同元素分组问题与不定方程解数问题

1. 正整数解个数

求将 $n$ 个完全相同的元素划分为 $k$ 组，每组至少有 $1$ 个元素的方法数；$n$ 个元素产生了 $n-1$ 个"空"，划分为 $k$ 组需要放 $k-1$ 个板子，因此答案为 $C^{k-1}_{n-1}$

问题等价于求 $x_1+x_2+\cdots+x_k=n$ 的正整数解组数

2. 非负整数解个数

求将 $n$ 个完全相同的元素划分为 $k$ 组，每组至少有 $0$ 个元素的方法数；按照"板子可以插在一起"这种思路不太好想，可以考虑将 全部 $\bm{k}$ 组每组增加一个元素，把非负整数解变成正整数解；这样问题转化为将 $n+k$ 个元素划分为 $k$ 组的正整数解，答案为 $C^{k-1}_{n+k-1} = C^{n}_{n+k-1}$

问题等价于求 $x_1+x_2+...+x_k=n$ 的非负整数解数

3. 不同下界整数解个数

求将 $n$ 个完全相同的元素划分为 $k$ 组，每组至少有 $a_k (\sum a_k \le n)$ 个元素的方案数；仿照上个情况的思想，将第 $k$ 组减少 $a_k$，将问题转化为将 $n-\sum a_k$ 个元素划分为 $k$ 组的非负整数解，答案为 $C^{k-1}_{n-\sum a_k+k-1} = C^{n-\sum a_k}_{n-\sum a_k+k-1}$

问题等价于求 $x_1+x_2+\cdots+x_k=n$ 的解数，其中 $x_i \ge a_i$

4. 不相邻的排列个数

求从 $1 \sim n$ 选出 $k$ 个互不相邻的整数的方案数；考虑先把 $k$ 个元素拿出来，再在这些元素中间添加一些元素使得其不相邻，拿出来的元素中间形成了 $k-1$ 个 下界为 $\bm{1}$ 的空，头尾各有一个 下界为 $\bm{0}$ 的空，总共有 $k+1$ 个空，答案为 $C^{k+1-1}_{n-k+1+1-1} = C^{k}_{n-k+1}$

P1771

求不定方程正整数解数模板题

P5520

可以直接套用 $4.$ 的公式；注意樱花树幼苗互不相同，因此答案需要多乘上 $m!$，为 $C^{m}_{n-m+1} \times m! = A^{m}_{n-m+1}$，不需要计算逆元了，直接边乘边模即可

3. 错排列与圆排列

错排列

对于 $1 \sim n$ 的排列 $P$，若 任意 $\bm{P_i}$ 都满足 $\bm{P_i \ne i}$，则称其为错排列；举个栗子，三元错排列有 $\{2, 3, 1\}$ 与 $\{3, 1, 2\}$

错排问题 (或称邮差问题)，指给定 $n$，求 $n$ 元错排列 $D_n$ 的个数；已知 $D_1=0, D_2=1$，仿照组合数递推式的推导方法，我们考虑其递推，有两种情况

1. 前 $\bm{n-1}$ 个元素全部错排

此时前 $n-1$ 个元素全部满足要求，只需处理不合法的第 $n$ 个元素；我们希望第 $n$ 个元素改变位置，那么可以将其 与前面的元素交换，容易发现任意交换都满足要求，因此方案数为 $(n-1) \times D_{n-1}$

2. 前 $\bm{n-1}$ 个元素有 $\bm{1}$ 个在其本来位置上，另外 $\bm{n-2}$ 个元素全部错排

设前 $n-1$ 个元素中在其本来位置上的元素为 $i$，此时我们 交换第 $\bm{i}$ 个与第 $\bm{n}$ 个元素，也能得到合法的方案；由于不合法的元素 $i$ 可以任取，方案数即为 $(n-1) \times D_{n-2}$

最终，我们得到了错排问题递推式

\[D_n = (n-1) \times (D_{n-1}+D_{n-2})\tag1 \]

其实错排问题还有其他递推式，常见的还有

\[D_n = nD_{n-1} \times (-1)^n\tag2 \]

下面给出证明，考虑作差，带入 $(1)$ 式，即得证

\[D_n-nD_{n-1} = (n-1) \times (D_{n-1}+D_{n-2}) - nD_{n-1}\\ = -[D_{n-1}-(n-1)D_{n-2}]\\ = (-1)^2[D_{n-2}-(n-2)D_{n-3}]\\ = ... = (-1)^{n-2}[D_2-2D_1] = (-1)^n \]

最后再不加证明地给出一个错排数通项公式

\[D_n = \lfloor \frac{n!}{e} \rfloor\tag3 \]

P4071

错排问题稍加变化，题意为求 $1 \sim n$ 的排列中恰好有 $m$ 个数在自己本来的位置上的方案数；首先先选出在自己位置上的 $m$ 个数，由于顺序固定，有 $C^{m}_{n}$ 种选法；对于剩下的 $n-m$ 个数，我们可以按照大小关系类似地视为 $1 \sim n-m$ 的错排列数，即 $D_{n-m}$

那么所求即为 $C^{m}_{n} \times D_{n-m}$；实现时，预处理阶乘 + 费马小定理求逆元求组合数，再按照上文提到的递推公式求错排列数即可

圆排列

$n$ 个元素排列成一个环形的不同方法数记为 $Q^n_{n}$，我们称两个圆排列相同当且仅当 所取元素相同 且元素 在环上的排列顺序一致

考虑直线排列与圆排列的关系，假设我们已经知道了所有要填入的元素及排列顺序，一共有 $n$ 个位置；首先在圆上按顺序填好元素，接下来我们可以通过多次旋转使得元素保持排列顺序不变；容易发现最多能够不重复地转 $n$ 次，因此一个圆排列实际上对应 $n$ 种不同的直线排列

圆排列 $Q^{n}_{n}$ 的计算公式即为

\[Q^{n}_{n} = \frac{A^{n}_{n}}{n} = (n-1)! \]

我们可以对结论进行推广，即 部分圆排列，求从 $n$ 个元素中选 $m$ 个排成环形的不同方法数，记为 $Q^{m}_{n}$

依照上面的思路，此时一个部分圆排列对应 $m$ 个直线排列，部分圆排列 $Q^{m}_{n}$ 的计算公式即为

\[Q^{m}_{n} = \frac{A^{m}_{n}}{m} = \frac{n!}{m \times (n-m)!} = \frac{n!(m-1)!}{m!(n-m)!} = C^{m}_{n} \times (m-1)! \]

CF1957E

题意为求 $\displaystyle \sum^{n}_{i=1} \sum^{i}_{j=1} C(i, j)$，其中 $C(i, j)$ 表示从 $i$ 个元素中选 $j$ 个的不同圆排列数

根据上文所述公式，有 $\displaystyle C(i, j) = C^{j}_{i} \times (j-1)!$；注意到式子中带有 $\bmod j$，因此我们考虑求和换序，将原式变形为求 $\displaystyle \sum^{n}_{j=1} \sum^{n}_{i=j} (C^{j}_{i} \times (j-1)! \bmod j)$

确定 $j$，根据数据范围，不难得知我们需要在不劣于 $O(\log n)$ 的时间复杂度内求出 $\sum^{n}_{i=j} (C^{j}_{i} \times (j-1)! \bmod j)$，考虑将其拆为两部分求解

首先考虑 $(j-1)! \bmod j$；当 $j$ 非素数时，令 $j = a \times b\ (2 \le a,b \le \frac{j}{2})$，我们进行分类讨论：

$a \ne b$，显然 $a$ 与 $b$ 都被包含在 $(j-1)!$ 内，此时贡献为 $0$
$a = b$ 且 $a \times 2 \ne j$，显然 $2 \times a$ 与 $b$ 都被包含在 $(j-1)!$ 内，此时贡献依然为 $0$
$a = b$ 且 $a \times 2 = j$，此时 $a=b=2, j=4$；由于 $3! \bmod 4 = 2$，此时贡献为 $2$

对于 $j$ 非素数的情况，只有 $j=4$ 时会对答案产生贡献，因此当 $j=4$ 时直接暴算所有 $C^{4}_{i}$ 即可

当 $j$ 为素数时，该式子即为 Wilson 定理，此时有$(j-1)! \bmod j = -1$，下面考虑此时如何计算 $\sum^{n}_{i=j} C^{j}_{i} \bmod j$；注意到组合数上恰有一个 $j$，是模数的倍数，这提醒我们可以使用 Lucas 定理进行简化；由 Lucas 定理，$\displaystyle C^{j}_{i} \bmod j = C^{1}_{ \lfloor i/j \rfloor} \times C^{0}_{i \% j} \bmod j = \lfloor i/j \rfloor \bmod j$

因此，对于 $i \in [k \times j, (k+1) \times j - 1]$，其贡献均为 $k$；我们可以枚举每个 $k$，将对应区间加上 $(-k \bmod j)$；进一步，我们可以将区间加转为差分解决，最终进行两次前缀和即可 (差分与求 $\sum j$ 各需要一次前缀和)

4. 抽屉原理 (鸽笼原理)

将 $n+1$ 个元素划分为 $n$ 组，则必然有一组至少有 $2$ 个元素；对其进行推广，将 $n$ 个元素划分为 $k$ 组，则必然有一组元素至少有 $\lceil \frac{n}{k} \rceil$ 个

UVA11237

首先将给定的 $a_i$ 全部模上 $c$，问题转化为构造一个位置集合 $S$ 使得 $(\sum_{i \in S} a_i) \bmod c = 0$；求得 $a_i$ 的前缀和 $s_i$，显然若 $s_i=0$，则 $S=\{1,2,3,\cdots,i\}$ 即满足要求；除掉 $s_i=0$ 的情况，$s_i$ 的所有可能取值有 $c-1$ 种，又因为题目保证 $c \le n$，根据抽屉原理，必然至少有一对 $\bm{s_i}$ 的取值相同；设其为 $s_p, s_q (p \le q)$，则 $S=\{p+1,p+2,\cdots, q\}$ 满足要求

综上，一定可以证明存在一些连续的位置满足要求，直接从前往后扫一遍即可

5. 二项式定理

二项式定理与二项展开式系数相关，定理内容为

\[(a+b)^n = \sum^{n}_{i=0} C^{i}_{n}a^{n-i}b^i \]

二项式定理证明

组合相关证明：

打开 $(a+b)^n$ 为 $(a+b) \times (a+b) \times ... \times (a+b)$，一共有 $n$ 项；每一项我们可以选择贡献 $a$ 或贡献 $b$，若要凑出 $a^{n-i}$，需要从 $n$ 项中选择 $n-i$ 个，方法数为 $C^{n-i}_{n}=C^{i}_{n}$；因此，$a^{n-i}b^i$ 项的系数为 $C^{i}_{n}$

数学归纳法证明：

在 $n=1$ 时，$(a+b)^1 = C^0_1a^1b^0+C^1_1a^0b^1$ 显然成立

不妨设 $n=m$ 时定理成立，即有

\[(a+b)^m = \sum^{m}_{i=0} C^{i}_{m}a^{m-i}b^i \]

在 $n=m+1$ 时，有

\[(a+b)^{m+1} = (a+b) \times (a+b)^{m}\\ = (a+b) \times \sum^{m}_{i=0} C^{i}_{m}a^{m-i}b^i \]

将 $a$ 与 $b$ 合并进去

\[= a \times \sum^{m}_{i=0} C^{i}_{m}a^{m-i}b^i + b \times \sum^{m}_{i=0} C^{i}_{m}a^{m-i}b^i\\ = \sum^{m}_{i=0} C^{i}_{m}a^{m-i+1}b^i + \sum^{m}_{i=0} C^{i}_{m}a^{m-i}b^{i+1} \]

分离出 $C^0_m$ 与 $C^m_m$ 两项，对其进行变形

\[= C^0_ma^{m+1}b^0 + \sum^{m}_{i=1} C^{i}_{m}a^{m-i+1}b^i + \sum^{m-1}_{i=0} C^{i}_{m}a^{m-i}b^{i+1} + C^m_ma^0b^{m+1}\\ = C^0_{m+1}a^{m+1}b^0 + \sum^{m}_{i=1} C^{i}_{m}a^{m-i+1}b^i + \sum^{m-1}_{i=0} C^{i}_{m}a^{m-i}b^{i+1} + C^{m+1}_{m+1}a^0b^{m+1}\\ = C^0_{m+1}a^{m+1}b^0 + \sum^{m}_{i=1} C^{i}_{m}a^{m-i+1}b^i + \sum^{m}_{i=1} C^{i-1}_{m}a^{m-i+1}b^{i} + C^{m+1}_{m+1}a^0b^{m+1} \]

根据组合数递推式 $C^m_n = C^m_{n-1}+C^{m-1}_{n-1}$，对求和柿子进行合并

\[= C^0_{m+1}a^{m+1}b^0 + \sum^{m}_{i=1} C^{i}_{m+1}a^{m+1-i}b^i + C^{m+1}_{m+1}a^0b^{m+1}\\ = \sum^{m+1}_{i=0} C^{i}_{m+1}a^{m+1-i}b^i \]

证毕

二项式定理推论

\[C^{0}_{n} + C^{1}_{n} + ... + C^{n}_{n} = \sum^{n}_{i=0} C^i_n = 2^n\tag1 \]

为 $a=b=1$ 时，即取 $(1+1)^n$ 时的特殊情况

\[\sum^{n}_{i=0} (-1)^iC^i_n = [n=0]\tag2 \]

为 $a=1,b=-1$ 时，即取 $(1+(-1))^n$ 时的特殊情况，注意 $n=0$ 时原式值为 $1$

二项式定理例题

P1313

二项式定理板子题；由二项式定理，$(ax+by)^k$ 中 $x^ny^m$ 项的系数即为 $C^m_k a^{k-m} b^m$

CF1332E

容易发现，只要所有格子的奇偶性相同，一定可以达到目标，与格子上有多少方块无关；本质上，我们 只需要考虑奇偶性

题目中操作 $1$ 只能使相邻的两格奇偶同时变化；实际上可以对该操作进行推广，任取两格 $p, q$ 与这两格间的一条路径 $p \rightarrow a_1 \rightarrow a_2 \rightarrow \cdots \rightarrow a_n \rightarrow q$ (格子 $p$ 与 $a_1$，$a_i$ 与 $a_{i+1}$，$a_n$ 与 $q$ 均相邻)，依次对路径上相邻的两格进行一次操作 $1$，即依次操作 $(p, a_1), (a_1, a_2), \cdots, (a_n, q)$；最终 $a_1, a_2, \cdots, a_n$ 上的值都恰好 $+2$，奇偶性不变，$p, q$ 上的值都恰好 $+1$，奇偶同时变化；因此，操作 $1$ 可以更改为选择任意两格使其奇偶性同时变化

我们对 $n \times m$ 的奇偶性进行分讨

$n \times m$ 为奇数；不妨设格子中填入了 $k_1$ 个奇数，$k_2$ 个偶数，有 $k_1 + k_2 = n \times m$，因此 $k_1$ 与 $k_2$ 必然有一个为偶数；这样我们可以把这偶数个奇数 (或偶数个偶数) 全部通过操作 $1$ 变成偶数 (或奇数)，再通过操作 $2$ 达到目标；因此，此时随便一种填法都满足要求，方案数为 $(R-L+1)^{nm}$
$n \times m$ 为偶数；仍然设格子中填入了 $k_1$ 个奇数，$k_2$ 个偶数，有 $k_1 + k_2 = n \times m$；注意到操作 $1$ 与操作 $2$ 不改变所有格子上方块数之和的奇偶性，而最终方块数之和必然为偶数，因此若 $k_1 \bmod 2 =1$，显然是不成立的；若 $k_1 \bmod 2 = 0$，则我们可以使用操作 $1$ 将所有的奇数变为偶数，即成立

因此，当 $n \times m$ 为奇数时可以 任意填入，方案数为 $(R-L+1)^{nm}$

当 $n \times m$ 为偶数时 必须填入偶数个奇数，在 $n \times m$ 个格子中选择 $k$ 个格子的方案数为 $C^k_{nm}$，设 $[L, R]$ 中有 $p$ 个奇数、$q$ 个偶数 ( $p+q = R-L+1$ )，则单次方案数为 $C^k_{nm} p^kq^{nm-k}$，将所有 $k$ 为奇数的方案累加即为总方案数

我们观察到这个柿子很像二项式定理，问题是 $k$ 一次会 $+2$ 而非 $+1$；我们考虑补全式子再减去多的部分，容易联想到二项式定理推论 $(2)$，答案即为

\[\frac{\sum^{nm}_{k=0} C^k_{nm}p^kq^{nm-k} - \sum^{nm}_{k=0} (-1)^kC^k_{nm}p^kq^{nm-k}}{2}\\ = \frac{(p+q)^{nm} - (p-q)^{nm}}{2} \]

直接快速幂即可，时间复杂度 $O(\log(nm))$

6. 容斥原理

设有 $n$ 种不同的属性，拥有第 $i$ 种属性的元素集合为 $S_i$，则有

\[\begin{aligned} \left|\bigcup_{i=1}^{n}S_i\right|=&\sum_{i}|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j\cap S_k|-\cdots\\ &+(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^{m}S_{a_i}\right|+\cdots+(-1)^{n-1}|S_1\cap\cdots\cap S_n| \end{aligned} \]

其中 $\cap$ 表示集合交运算，$\cup$ 表示集合并运算

另一种表达为

\[\left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right| \]

可以理解为逐层去掉重复的部分，再补回多减的部分

容斥原理证明

对于任一元素 $P_i$，设其出现在了集合 $S_1, S_2, \cdots S_m$ 中，则其被统计的次数为

\[C^1_m-C^2_m+\cdots+(-1)^{m-1}C^m_m \]

为什么呢？相当于我们分别统计 $|S_i|, |S_i \cap S_{j}|, \cdots$ 产生的贡献，元素在其中任一个集合交结果中的出现次数都是 $1$，则不考虑正负系数情况下贡献也是 $1$，因此可以直接统计怎么选

观察到柿子很像二项式定理推论 $(2)$，尝试进行变形

\[C^1_m-C^2_m+\cdots+(-1)^{m-1}C^m_m\\ = C^0_m - \sum^{m}_{i=0} (-1)^iC^i_m\\ = 1 - (1-1)^m = 1 \]

则每个元素刚好被统计一次，证毕

容斥原理推论

设全集为 $U$，若求全集中不具有任一性质的元素的个数，则有筛法公式

\[\left|\bigcap_{i=1}^{n} \overline{S_i} \right| = \left|U\right|-\left|\bigcup_{i=1}^{n}S_i\right|\tag1 \]

其中 $\overline{S}$ 表示集合 $S$ 的补集 (补集 $\overline{S}$ 是由 $U$ 中所有不属于 $S$ 的元素组成的集合)

若求集合的交，可以用 全集减去补集的并集，证明显然

\[\left|\bigcap_{i=1}^{n}S_i\right| = \left|U\right| - \left|\bigcup_{i=1}^{n}\overline{S_i}\right|\tag2 \]

公式 $(1), (2)$ 右侧均可以使用容斥原理进一步变形

容斥原理例题

P1450

其实这题乍一看很像插板，但是实际上这题 限制了上界而非下界，第 $i$ 种硬币最多能取 $d_i$ 个，因此考虑容斥

我们令属性 $P_i$ 表示限制第 $i$ 种硬币取的数量 $\le d_i$，同时其他硬币取的数量可以为任意非负整数；记集合 $S_i$ 包含所有拥有属性 $P_i$ 的选择方法，答案即为

\[\left|\bigcap_{i=1}^{n}S_i\right| \]

可以先用容斥原理推论 $(2)$ 将其变形为

\[\left|\bigcap_{i=1}^{n}S_i\right| = \left|U\right| - \left|\bigcup_{i=1}^{n}\overline{S_i}\right| \]

其中 $\overline{S_i}$ 拥有的属性即为：限制第 $i$ 种硬币最少取 $d_i+1$ 个，同时其他硬币取的数量可以为任意非负整数；这可以应用插板法的思想 —— 减去多出的下界 来解决

另外对于求容斥中一些集合 $\overline{S_{a_i}}$ 的交，可以转化为以下不定方程的解数

\[\sum^4_{i=1} C_id_i = S - \sum^k_{i=1}C_{a_i}(d_{a_i}+1) \]

其中 $S$ 为要达到的目标；而 $S - \sum^k_{i=1}C_{a_i}d_{a_i}$ 为一个可以算出来的值，显然这是可以预处理的，这样就做完了

预处理时间复杂为 $O(4S)$，询问时间复杂度为 $O(2^4n)$，总时间复杂度为 $O(4S+2^4n)$

P5664

简要题意为给定一个 $n$ 行 $m$ 列的矩阵 $a[i][j]$ ，在其中选取 $k$ 行，每行只能取一个元素，每列最多取 $\lfloor \frac{k}{2} \rfloor$ 个元素；一种选法的贡献为所有被选的元素之积，最终求所有选法的贡献和

每列最多取 $\lfloor \frac{k}{2} \rfloor$ 个元素的限制其实不是特别好处理，考虑反面；我们观察到 最多只有一列 能够超出限制，因此直接枚举该列即可，将其记为 $col$

不妨设选择的方案中在 $col$ 列上选了 $res_1$ 个，其他列上选了 $res_2$ 个；如何判断当前列超出限制？由于此时总数 $k$ 即为 $res_1+res_2$，因此直接判断是否有 $res_1>res_2$ 即可

考虑 $dp$；由于我们 只关心 $\bm{res_1}$ 与 $\bm{res_2}$ 的大小关系，令 $dp[i][j]$ 表示当前考虑到第 $i$ 行，$res_1 - res_2 = j$ 的总方法数；对于第 $i$ 行，我们有三种处理方式：

不在这一行选择任何元素；此时 $dp[i][j] += dp[i-1][j]$
在这一行的第 $col$ 列选择元素，上一行的 $res_1 - res_2$ 应该减少 $1$；此时 $dp[i][j] += dp[i-1][j-1] \times a[i][col]$
在这一行的其他列选择元素，上一行的 $res_1 - res_2$ 应该增加 $1$；此时 $dp[i][j] += dp[i-1][j+1] \times (\sum_{t \ne col} a[i][t])$

初始条件即什么都不选时，$dp[0][0]=1$

实现时，$\sum_{t \ne col} a[i][t]$ 可以预处理，另外注意 $res_1-res_2$ 可能小于 $0$，可以将第二维全部向右偏移 $n$；统计答案时累加所有第二维为正的结果即可，即 $\sum^{n+n}_{i=n+1} dp[n][i]$

对于总贡献，我们也能够采用类似的 $dp$ 策略，设 $total[i][j]$ 表示到第 $i$ 行总共选择了 $j$ 个数的方法数；类似的，转移为 $total[i][j] += total[i-1][j]$ 或 $total[i][j] += total[i-1][j-1] \times \sum^{n}_{t=1} a[i][t]$；

初始条件为 $dp[i][0]=1$，表示到第 $i$ 行全部都不选

实现时，求和仍然可以预处理，统计答案时累加即可，即为 $\sum^{n}_{i=1} total[n][i]$

P2567

相比上一题，这道的容斥味就很浓了

首先，我们预处理出所有 互不为倍数 的幸运号码，为下一步容斥做准备；为什么要求互不为倍数？因为如果一个数既是幸运号码又是近似幸运号码，我们只需统计其作为近似号码的贡献，避免重复；实现时直接用 bfs 即可，总情况不超过 $2^{10}$

实际上，去掉不符合条件的数后一共有 $943$ 个幸运号码；如果按照硬币购物的思路，我们需要从 $1$ 枚举到 $2^{943}$，显然是不可取的；观察到这些情况中有不少是不会产生贡献的，具体的，设我们统计 $a_1, a_2,\cdots, a_n$ 这些幸运号码在 $[a, b]$ 中的公倍数个数，若 $lcm(a_1, a_2, \cdots, a_n) > b$ 显然就不会有任何贡献

因此，我们考虑改用 dfs；仍然维护当前的 $pos$ (走到哪一步)，$lcm(a_i)$ (所有已选幸运号码的公倍数) 与 $cnt$ (表示已经选了多少个幸运号码)，当走到结尾时，贡献即为 $\displaystyle \lfloor \frac{b}{lcm(a_i)} \rfloor - \lfloor \frac{a-1}{lcm(a_i)} \rfloor$

别忘了在公倍数 $ > b$ 时进行剪枝；实现时，我们可以先将幸运号码 从大到小排序，使不合法情况尽早出现。另外注意 $lcm$ 可能爆 long long，可以开 int128 或者变 long double 解决

~~时间复杂度不会算~~，但是由于 $lcm$ 的增长速度很快，应该没什么问题

P5123

观察到位置数只有 $5$，因此我们考虑对于每一头牛，对其与之前的牛的重复号码位置进行容斥

仍然使用类似硬币购物的思路，用一个取值范围为 $[1, 2^5-1]$ 的二进制数代表每位选/不选，判断每位是否为 $1$ 即可

那么我们如何判断选出的数与之前产生重复？有一种很暴力的想法就是开五个套起来的 map，第 $i$ 个套 $i$ 层，处理选择 $i$ 个数的情况；但这么做很麻烦，其实有一个更好的办法：哈希。注意，由于统计答案时本质上是无序的，但选择的顺序会影响哈希的结果，因此需要 先对给出的号码进行排序

实现时，可以使用多项式哈希或者直接转成字符串再哈希；若使用多项式哈希记得把进制数开大点，同时建议使用自然溢出，~~我被卡了好几次~~

P5505

我们设属性 $P_i$ 表示：有 $i$ 名同学一定没有特产，其余 $n-i$ 名同学可能有特产也可能没有特产的方法数；设集合 $S_i$ 包含所有满足属性 $P_i$ 的分配方法

显然 $S_0$ 会包含 $S_1$，$S_1$ 会包含 $S_2$，$\cdots$，$S_i$ 会包含 $S_{i+1}$；因此我们考虑使用容斥去掉它们之间重叠的部分

那么假设确定一定没有被分到特产的同学数 $p$，如何求出 $\left|S_p\right|$？这本质上就是 插板法。设 $k = n-p$，我们先选出 $k$ 个可能能够分到特产的同学，有 $C^{k}_{n}$ 种选法；接下来等价于对于所有 $i (1 \le i \le m)$ 种特产求不定方程 $x_1 + x_2 + \cdots + x_k = a_i$ 的 非负整数解数，根据插板法即为 $C^{k-1}_{a_i+k-1}$；而每种特产间相互独立，总方案数即为 $\displaystyle C^k_n \times \prod^{m}_{i=1} C^{k-1}_{a_i+k-1}$

回到总体上，类比容斥原理，其实这里的 $\left|S_p\right|$ 类似于所有选 $p$ 个集合交起来的结果之和，即 $\displaystyle \sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^pS_{a_i}\right|$；因此最终的答案即为 $\displaystyle \sum^{n-1}_{i=0} (-1)^i \left|S_i\right|$

实现时，预处理出阶乘即可，另外注意取模不要取成负数；时间复杂度 $O(nm)$

7. 卡特兰数

卡特兰数定义为一个数列 $H_n$，其中 $H_0 = H_1 = 1$，有如下的递推公式与组合公式

递归定义：

\[H_n = \sum^{n-1}_{i=0} H_{i}H_{n-1-i}\tag1 \]

递推公式：

\[H_n = \frac{H_{n-1} \times (4n-2)}{n+1}\tag2 \]

组合公式 $(1)$：

\[H_n = \frac{C^n_{2n}}{n+1}\tag1 \]

组合公式 $(2)$：

\[H_n = C^n_{2n} - C^{n-1}_{2n}\tag2 \]

卡特兰数证明

由递归定义推到组合公式需要用到生成函数等知识，具体证明过程可以参考神奇的卡塔兰(Catalan)数

两组合公式间互推是比较简单的，如下

\[C^{n}_{2n} - C^{n-1}_{2n} = \frac{(2n)!}{n! \times n!} - \frac{(2n)!}{(n-1)! \times (n+1)!} = \frac{(2n)!}{n! \times n!} \times (1 - \frac{n}{n+1}) = \frac{C^n_{2n}}{n+1} \]

由组合公式，可以进而证明递推公式

\[\frac{H_{n-1} \times (4n-2)}{n+1}\\ = \frac{C^{n-1}_{2(n-1)} \times (4n-2)}{n \times (n+1)}\\ = \frac{(2n-2)! \times (4n-2)}{(n-1)! \times (n-1)! \times n \times (n+1)}\\ = \frac{(2n)! \times 2}{(n-1)! \times (n+1)! \times 2n}\\ = \frac{(2n)!}{n! \times (n+1)!} = H_n \]

反过来，递推公式一直迭代下去也可以得到组合公式

\[H_n = \frac{4n-2}{n+1} \times H_{n-1}\\ = \frac{4n-2}{n+1} \times \frac{4(n-1)-2}{n-1+1} \times H_{n-2}\\ = \cdots\\ = H_0 \times \prod^{n}_{i=1} \frac{4i-2}{i+1}\\ = 2^n \times \frac{1 \times 3 \times \cdots \times (2n-1)}{(n+1)!}\\ = \frac{(2n)!}{n! \times (n+1)!} = \frac{C^n_{2n}}{n+1} \]

那么这些公式就都是等价的

卡特兰数应用

1. 不相交弦问题

给定圆上的 $2n$ 个点，求使得将其两两连接得到的 $n$ 条线段不相交的方法数

连接一对点，实际上会将整个圆切成两半，接下来连接的每对点必然处于同一部分中；因此这就是一个完全相同的子问题，递归式为 $dp_n = \sum^{n-1}_{i=0} dp_{i}dp_{n-1-i}$，其中 $i$ 与 $n-1-i$ 的意义为切开后两边的点对数

注意到这是卡特兰数的递归定义，因此答案即为 $H_n$

板子题：P1375

1.1 二叉树计数

给定 $n$ 个点，求可以构造多少个不同的二叉树

类似的，选择一个点为根会把整棵树切成左子树和右子树，变为完全相同的问题；设左子树有 $i$ 个节点，右子树有 $n-1-i$ 节点，则有 $dp_n = \sum^{n-1}_{i=0} dp_{i}dp_{n-1-i} = H_n$

1.2 凸多边形的三角划分

给定一个凸 $n+2$ 边形，求用 $n-1$ 条不相交的直线连接起各对顶点，且这些直线互不穿过，将多边形划分成 $n$ 个三角形的方法数

同样的，我们选取一条边，枚举其往哪个顶点 (与当前边的两顶点互异) 连边；这会将原多边形划分为一个 $i+2$ 边形与一个 $n-1-i+2$ 边形，去掉 $+2$，实际上就是卡特兰数

为什么 $(i+2)+(n-1-i+2) \ne n+2$？这是由于我们去掉了原多边形的一条边，又在多边形内部连了两条边，因此比之前增加了一条边

2. $\bm{\pm1}$ 数列问题

求有多少个由 $n$ 个 $+1$ 与 $n$ 个 $-1$ 构成的任意前缀和总是非负数的数列 $a_1, a_2, \cdots, a_{2n}$

我们考虑其反面情况，即求有多少个这种数列使得其存在前缀和是负数；不妨用 最靠前的 不合法位置来统计，即取一个 $m (1 \le m \le 2n)$，使得 $\sum^{m}_{i=1} a_i < 0$ 且对于任意 $1 \le k < m$，满足 $\sum^{k}_{i=1} a_i \ge 0$

问题即转化为求所有满足如下条件的数列数量：

\[\begin{cases} \ a_1+a_2+\cdots+a_m < 0\\ \ a_1+a_2+\cdots+a_{2n} \ge 0\\ \end{cases} \]

我们注意到，由于 $m$ 是最靠前的不合法位置，那么一定有 $a_1+a_2+\cdots+a_m = -1$，这也可以推出 $a_{m+1}+a_{m+2}+\cdots+a_{2n} = 1$；因此，我们考虑 构造另一个长度为 $\bm{2n}$ 的数列 $\bm{b}$，满足当 $1 \le i \le m$ 时有 $b_i = -a_i$，当 $m < i \le 2n$ 时有 $b_i = a_i$

容易发现构造出的 $b$ 数列是和不合法的 $a$ 数列 一一对应 的；观察其性质，易得 $b_i \in \{1, -1\}$ 且 $\sum^{2n}_{i=1} b_i = 2$，由此可以进一步推出 $b$ 中有 $n+1$ 个 $1$、$n-1$ 个 $-1$；

因此，$b$ 数列的数量 (即不合法的 $a$ 数列的数量) 为 $C^{n-1}_{2n}$；又由于总共有 $C^n_{2n}$ 种情况，满足要求的 $a$ 数列就一共有 $C^{n}_{2n} - C^{n-1}_{2n}$ 种

这就是卡特兰数的组合公式，所以求的仍然是 $H_n$

板子题：P1722

2.1 合法栈序列数量

有 $n$ 个元素，初始时栈为空，每次操作可以选择 push 或 pop，求合法的操作序列数

将 push 操作看作 $+1$，pop 操作看作 $-1$ 即可

板子题：P1044

2.2 买票问题

有 $2n$ 个人来买票，$n$ 个人持有面值为 $k$ 的钱，另外 $n$ 个人持有面值为 $2k$ 的钱；一张票 $k$ 块钱，限定每人只能买一张；售票处开始时没有钱，求有多少种排队方式使得售票处在任何时候不会找不出钱

将持有 $k$ 块钱的人买票看作 $+1$，持有 $2k$ 块钱的人买票看作 $-1$ 即可

板子题：P1754

2.3 格路计数

有一网格图，每一步只能向上走或向右走，求从点 $(0, 0)$ 走到 $(n, n)$ 且不穿过直线 $y=x$ 有多少种走法

将向上走看作 $-1$，向右走看作 $+1$，等价于 $\pm 1$ 序列问题

其实也有另一种理解方法：考虑反面，用第一次解除 $y=x+1$ 的点 $P$ 统计每条不合法路径，可以将点 $P$ 到终点的路径按照 $y=x+1$ 翻转，这样每条不合法路径的终点都是点 $(n-1, n+1)$

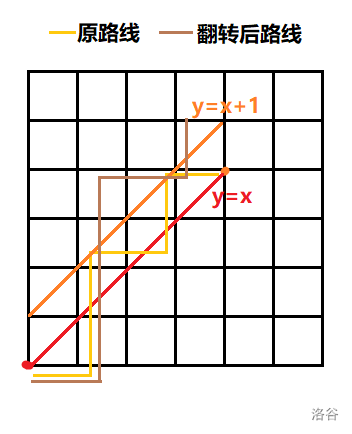
格路计数图片

从 $n-1+n+1 = 2n$ 次向前/向上中选择向前走的 $n-1$ 次，不合法路径的条数即为 $C^{n-1}_{2n}$；类似的，总路径数为 $C^{n}_{2n}$，答案即为 $C^{n}_{2n} - C^{n-1}_{2n} = H_n$

卡特兰数例题

P2532

我们需要选取 $N$ 个钢材搭建高度为 $N$ 的阶梯，注意到一个钢材不可能包含整个阶梯 $\ge 2$ 阶，因此 恰好一个阶梯包含一阶

我们尝试将原问题划分为同样的子问题，考虑枚举 含有整个阶梯左下角 的钢材的右上角在哪上，因为它能够完全分开上下两部分；注意到分开后恰形成了两个完全相同的子问题，于是递推式即为 $dp_i = \sum^{n-1}_{i=1} dp_idp_{n-1-i}$，可以结合下图理解

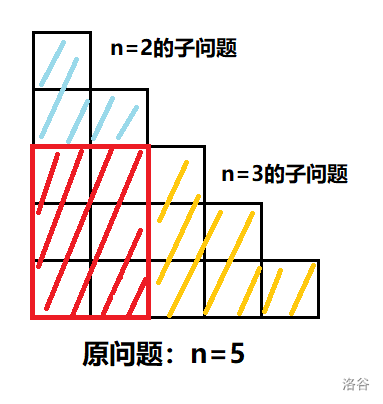
P2532 图片

初值显然有 $dp_1 = 1$，答案实际上就是卡特兰数 $H_n$

P1641

考虑转化为格路计数

由于 $1$ 的数量必须大于等于 $0$ 的数量，我们设填入 $1$ 代表向前走一步，填入 $0$ 代表向上走一步；因此题目转化为，从出发点 $(0,0)$ 走到终点 $(n, m)$ 不穿过直线 $y=x$ (也就是不碰到直线 $y=x+1$) 的方案数

使用类似的处理方法，我们考虑反面，将第一次穿过 $y=x$ 及以后的路径按照直线 $y=x+1$ 翻转；根据几何知识，这样的路径的终点均为 $(n+1, m-1)$，与原来的不合法路径一一对应

因此不合法路径有 $C^{n+1}_{n+m}$ 条，总共有 $C^{n}_{n+m}$ 条，答案即为 $C^{n}_{n+m} - C^{n+1}_{n+m}$

P3200

事实上打表容易发现答案就是卡特兰数

证明放在后面，先说实现；这题有个很坑的点在于不保证 $p$ 为质数，有可能没有逆元。那么怎么求卡特兰数？一种很朴素的想法是分解质因数 + EXCRT；这有点麻烦，事实上我们可以更加直接一点：处理出所有出现的质数及其指数，最终快速幂求乘积即可，这样就绕过了除法

具体的，使用组合公式，答案即为 $\displaystyle \frac{C^{n}_{2n}}{n+1} = \frac{(2n)!}{n! \times (n+1)!} = \frac{\prod^{2n}_{i=n+2} i}{n!}$；对于每个乘数分解质因数，维护含有的质数的指数即可

接下来给出答案即为卡特兰数 $H_n$ 的证明；分析性质，容易得出奇数项递增、偶数项递增 (废话)，且 所有偶数项上的数都比其前面所有的数大，也就是 大于等于其下标

考虑从小到大依次填入 $1-2n$；由于填入的数严格递增，奇数项与偶数项间不能出现"空着"的位置，即每个数只能填入最靠前的空着的奇数项或偶数项，同时也要满足前面推出的对偶数项的限制

可能有点绕，举个栗子：假设已经在第 $1$ 位填入 $1$、第 $2$ 位填入 $2$，$3$ 理论上可以填在第 $3$ 位上 (最靠前的奇数位) 也可以填在第 $4$ 位上 (最靠前的偶数位)，但由于 $3<4$，实际上它不能填在第 $4$ 位上

我们尝试更具象地表述这一偶数项的限制；设我们目前填入了 $1-k$，令 $p_1$ 表示前面填入了多少个奇数项，$p_2$ 表示前面填入了多少个偶数项 ( $p_1+p_2=k$ )；显然下标最大的偶数项值为 $val = 2 \times p_2$，那么需要满足 $val \ge p_1+p_2$，也就是 $\bm{p_2 \ge p_1}$！

这个性质我们已经非常熟悉了，就是前面讲过的 $\pm 1$ 问题，放在偶数项上视为 $+1$，放在奇数项上视为 $-1$，因此答案即为 $H_n$

P3978

记 $n$ 个节点形成的不同构二叉树的叶子数量之和为 $f_n$，形成的不同构数量为 $H_n$ (就是卡特兰数)，题意即为给定 $n$，求 $\frac{f_n}{H_n}$

事实上打表容易发现 $f_n = n \times H_{n-1}$

下面给出证明；我们考虑 $n$ 个节点的二叉树与 $n-1$ 个节点的二叉树间的递推关系，显然就是 $n-1$ 个节点的二叉树又添了个节点 (废话)；由于添上一个节点后形成的二叉树必然有叶子 (还是废话)，因此我们一定可以通过 将 $\bm{n}$ 个节点的二叉树删去一个叶子 覆盖所有的 $n-1$ 个节点组成的二叉树

所以 $f_n = H_{n-1}$ ...吗？显然不是；删去一个叶子，得到的 $n-1$ 个节点组成的二叉树可能重复；我们想要通过 $H_{n-1}$ 推到 $f_n$，就得知道第 $i$ 个 $n-1$ 个节点的二叉树重复出现的次数 $p_i$，这样就有 $f_n = \sum^{H_{n-1}}_{i=1} p_i$

那么为什么会造成重复？$n-1$ 个节点组成的二叉树上可能能挂很多个叶子，删掉这些挂上的不同的叶子就引起了重复；这样问题转化为 可以挂多少个叶子

不妨设原 $n-1$ 个节点组成的二叉树上儿子数为 $0$ 的节点个数为 $num_0$，儿子数为 $1$ 的节点个数为 $num_1$，儿子数为 $2$ 的节点个数为 $num_2$；由于树有 $n-1$ 个点 $n-2$ 条边，容易得到以下关系式

\[\begin{cases} num_0 + num_1 + num_2 = n-1\\ 0 \times num_0 + 1 \times num_1 + 2 \times num_2 = n-2 \end{cases} \]

两式相减，得到 $num_0 - num_2 = 1$；原二叉树上儿子数为 $0$ 的点可以挂两个叶子，儿子数为 $1$ 的点可以挂一个叶子，儿子数为 $2$ 的点不能挂叶子；因此总共能挂 $\bm{p_i = 2 \times num_0 + 1 \times num_1 + 0 \times num_2 = num_0 + num_1 + (num_2 + 1) = n}$ 个叶子

那么重复次数 $p_i$ 均为 $n$，即有 $f_n = n \times H_{n-1}$，得证

最终答案即为

\[\frac{f_n}{H_n} = \frac{n \times H_{n-1}}{H_n} = \frac{n \times (n+1) \times C^{n-1}_{2n-2}}{n \times C^{n}_{2n}} = \\\frac{(2n-2)! \times n! \times n! \times (n+1)}{(2n)! \times (n-1)! \times (n-1)!} = \frac{n \times n \times (n+1)}{(2n-1) \times 2n} = \frac{n^2+n}{4n-2} \]

8. 康托展开

给定一个 $\bm{1 \sim n}$ 的排列，将其按照字典序排序，可以使用康托展开求其排名

在一些问题中 (如之前做过的八数码问题) 中，可以用康托展开进行状态压缩，方便判断是否走到过；其实 FA 告诉我说这个东西之前汪老师讲过，因此我就 ~~再讲一遍~~

算法的过程其实还蛮好理解的；设我们当前处理排序后排列的第 $i$ 位 ($1 \le i \le n$)，当前位上的值为 $val[i]$；显然，所有第 $i$ 位为 $1 \sim val[i]-1$ 的其他排列都在当前排列之前，除去第 $i$ 位上的数和之前填好的数，剩余的 $n-i$ 个数可以在后面的 $n-i$ 个位置中随意排列，有 $\bm{(n-i)!}$ 种填法

接下来考虑第 $i$ 位能够填什么；首先，它必须为 $1 \sim val[i]-1$ 中的一个数，这样才能保证在当前排列前面；其次，它不能和之前填好的 $i-1$ 个数 (也就是 $val[1], val[2], \cdots, val[i-1]$) 相同。于是我们需要处理出 在 $\bm{1 \sim val[i]-1}$ 中有多少个数已经在前面被填入了，可以使用 树状数组 解决

设前面有 $k$ 个数已经被填入，贡献即为 $(val[i]-1-k) \times (n-i)!$，从 $1$ 到 $n$ 枚举 $i$，累加贡献即可；注意这样我们求出的是在当前排列前面的排列的数量，最终 还要 $\bm{+1}$

时间复杂度 $O(n \log n)$

P5367

康托展开模板

9. 多重集的排列数与组合数

多重集，顾名思义，本质上是广义的集合，可以包含重复的元素；具体的，设多重集 $S$ 中一共含有 $n$ 个元素，有 $k$ 种不同元素，第 $i$ 种元素的值为 $v_i$、有 $c_i$ 个，则可以表示为 $S = \{c_1 \cdot v_1, c_2 \cdot v_2, \cdots, c_k \cdot v_k\}$

多重集的排列数

对于含有 $n$ 个元素、$k$ 种不同元素的多重集 $S = \{c_1 \cdot v_1, c_2 \cdot v_2, \cdots, c_k \cdot v_k\}$，其所有 $n$ 个元素的 全排列数 即为它们组成的多重集的组合数；这里不能直接简单的用 $n!$ 计算，因为对于每 $c_i$ 个相同元素，这么算实际上 认为它们是互不相同的。本来这些元素只会产生 $1$ 个贡献，这样算会认为它们产生了 $c_i!$ 个贡献；那么真实的结果应该是 $\displaystyle \frac{n!}{\prod^{k}_{i=1} c_i!}$

多重集的组合数

对于含有 $n$ 个元素、$k$ 种不同元素的多重集 $S = \{c_1 \cdot v_1, c_2 \cdot v_2, \cdots, c_k \cdot v_k\}$，在其中选出 $r$ 个元素的方案数即为多重集的组合数

若对于任意 $1 \le i \le k$ 都有 $r \le c_i$，问题即简化为：枚举 $i (1 \le i \le k)$，在第 $i$ 种元素中选择 $x_i$ 个使得 $\sum^{k}_{i=1} x_i = r$ 的方案数；这就是之前讲过的不定方程的非负整数解数，结果即为 $C^{k-1}_{r+k-1}$

考虑进行推广；如果对 $r$ 没有限制，又该如何求解？仍然考虑转化为不定方程解数，即 $\sum^{k}_{i=1} x_i = r$，区别在于这里限制 对于任意 $\bm{1 \le i \le k}$，有 $\bm{x_i \le c_i}$；这其实和硬币购物那题挺像的，由于限制下界容易解决，我们使用容斥原理将上界转化为下界

具体的，设属性 $P_i$ 表示限制 $x_i \le c_i$，且其他 $x_j (i \ne j)$ 都为非负整数；记集合 $S_i$ 包含所有拥有属性 $P_i$ 的选择方法，答案即为

\[\left|\bigcap_{i=1}^{k}S_i\right| \]

同样使用容斥原理推论 $(2)$，变形为

\[\left|\bigcap_{i=1}^{k}S_i\right| = \left|U\right| - \left|\bigcup_{i=1}^{k}\overline{S_i}\right| \]

这里 $\left|U\right|$ 即为原不定方程的非负整数解数，易知为 $C^{k-1}_{r+k-1}$

使用容斥原理展开右侧，我们还需要求一些补集的交；设这些补集为 $a_1, a_2, \cdots, a_p (1 \le p \le k)$，根据插板法，第 $a_i$ 个空的下界为 $c_{a_i}+1$ (注意要 $\bm{+1}$)，其余空的下界为 $0$，我们只需要减去多出的下界，转化为求非负整数解数；那么这些补集的交即为 $C^{k-1}_{r-\sum^{p}_{i=1} (c_{a_i}+1)+k-1}$

最终根据容斥原理计算即可

CF451E

多重集的组合数 (推广) 板子题

这里 $n$ 很小，$s$ 很大，算 $C^{n-1}_{s-\sum^{p}_{i=1} (f_{a_i}+1)+n-1}$ 的时候分子只有 $n-1$ 项，完全可以直接暴算，但注意乘数可能很大，需要提前取模；事实上我们求的所有组合数的分母都是 $(n-1)!$，因此可以 预处理逆元 进行优化