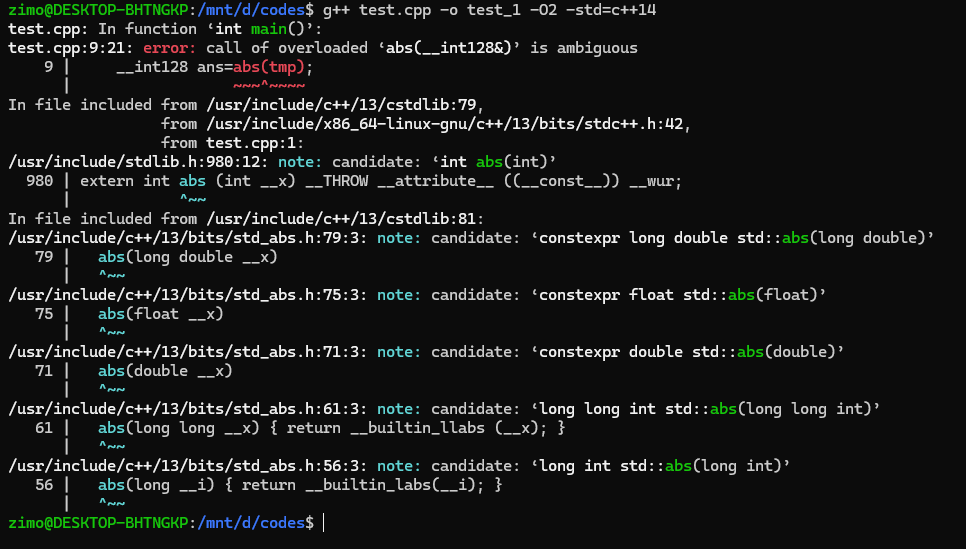
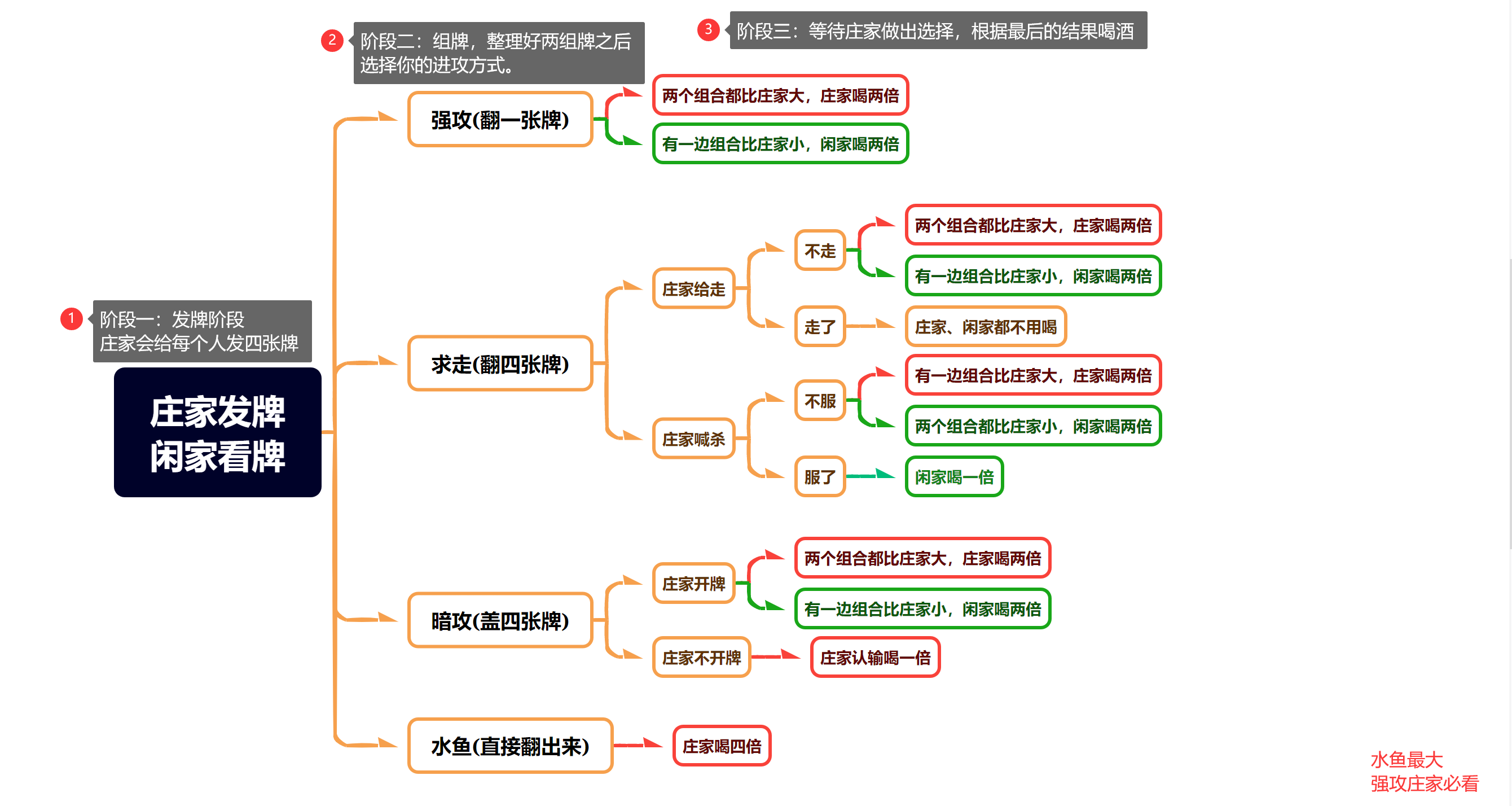
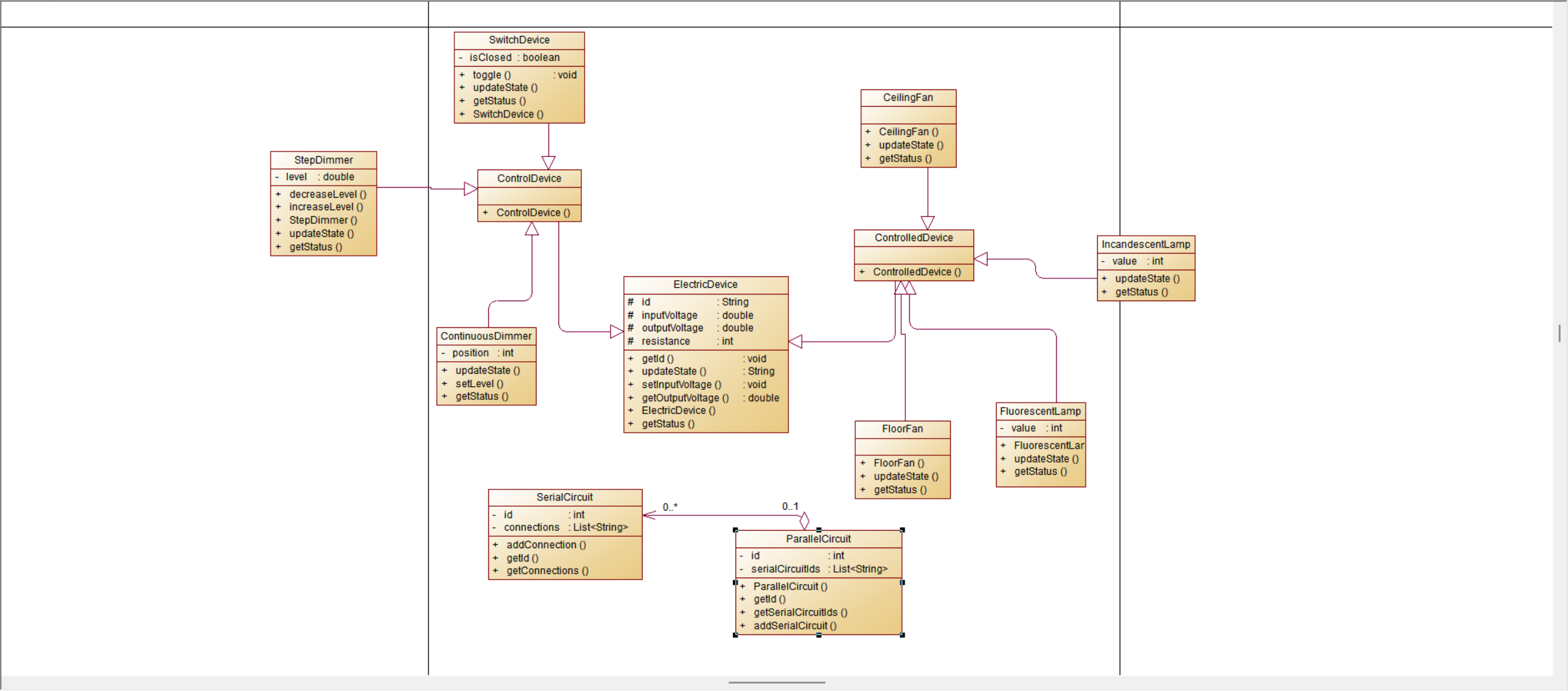
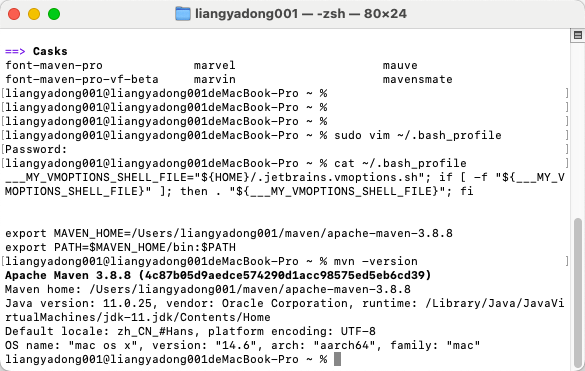
一签三计数,罚坐了。
草莓
简单贪心,随便贪就过了。
点此查看代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALFILE *InFile = freopen("in.in","r",stdin),*OutFile = freopen("out.out","w",stdout);
#else// FILE *InFile = stdin,*OutFile = stdout;FILE *InFile = freopen("guiltiness.in","r",stdin),*OutFile = freopen("guiltiness.out","w",stdout);
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
const int N = 2e5 + 10;
int n,m,a[N],b[N];
inline void solve(){cin>>n>>m;rep(i,1,n-1,1) cin>>a[i];rep(i,1,m-1,1) cin>>b[i];sort(a+1,a+n,greater<int>());sort(b+1,b+m,greater<int>());ll ans = 0;int na = 1,nb = 1,ta = 0,tb = 0;while(na < n && nb < m){if(a[na] >= b[nb]) ans += 1ll*(tb+1)*a[na],na++,ta++;else ans += 1ll*(ta+1)*b[nb],nb++,tb++;}while(na < n) ans += 1ll*(tb+1)*a[na],na++,ta++;while(nb < m) ans += 1ll*(ta+1)*b[nb],nb++,tb++;cout<<ans;
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);solve();
}
三色
弱化版:[ARC074E] RGB Sequence
先考虑\(O(n^3)\)怎么做。
设\(f_{i,j,k}\)表示上一个与\(a_{i}\)颜色不同的位置为\(j\),上一个与\(a_i,a_j\)颜色都不同的位置为\(k\)时的方案数。
发现一定有 \(i>j>k\)(当\(i=1\)时除外,此时\(j=k=0\)),且 \(f_{1,0,0}=3\)。
考虑如何从 \(i\) 转移到 \(i+1\):
- \(a_{i+1}=a_{i}\),那么\(f_{i+1,j,k}+=f_{i,j,k}\)
- \(a_{i+1}=a_{j}\),那么\(f_{i+1,i,k}+=f_{i,j,k}\)
- \(a_{i+1}=a_{k}\),那么\(f_{i+1,i,j}+=f_{i,j,k}\)
考虑如何剔除不合法状态,其实就是将不合法的状态置为 \(0\),将一个形如 \((l,r,x)\) 的限制挂在 \(r\) 上,对\(x\)进行分讨。
- \(x=1\),那么\(j<l\)。
- \(x=2\),那么\(k<l,j\le l\)。
- \(x=3\),那么\(l\le k<j\)。
保留这些合法状态,其他的置为 \(0\) 即可。
点此查看代码
//[ARC074E] RGB Sequence
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALFILE *InFile = freopen("in.in","r",stdin),*OutFile = freopen("out.out","w",stdout);
#elseFILE *InFile = stdin,*OutFile = stdout;// FILE *InFile = freopen("color.in","r",stdin),*OutFile = freopen("color.out","w",stdout);
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
const int N = 5e2 + 10,M = 1e6 + 10,mod = 1e9 + 7;
struct limit{int l,x;};
vector<limit> lim[N];
int n,m,f[N][N][N];
inline void solve(){cin>>n>>m;rep(i,1,n,1) vector<limit> ().swap(lim[i]);rep(i,1,m,1){int l,r,x;cin>>l>>r>>x;lim[r].push_back({l,x});}rep(i,0,n,1) rep(j,0,n,1) rep(k,0,n,1) f[i][j][k] = 0;f[1][0][0] = 3;rep(i,1,n,1){for(auto [l,x]:lim[i]) rep(j,0,i-1,1){int lmt = j-(!!j);rep(k,0,lmt,1){if(x == 1 && l <= j) f[i][j][k] = 0;if(x == 2 && (l <= k || j < l)) f[i][j][k] = 0;if(x == 3 && k < l) f[i][j][k] = 0;}}if(i == n) break;rep(j,0,i-1,1){int lmt = j - (!!j);rep(k,0,lmt,1){if(!f[i][j][k]) continue;f[i+1][j][k] = (f[i+1][j][k] + f[i][j][k])%mod;f[i+1][i][k] = (f[i+1][i][k] + f[i][j][k])%mod;f[i+1][i][j] = (f[i+1][i][j] + f[i][j][k])%mod;}}}int ans = 0;rep(j,0,n-1,1){int lmt = j - (!!j);rep(k,0,lmt,1) ans = (ans + f[n][j][k])%mod;}cout<<ans<<'\n';
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);int T = 1;while(T--) solve();
}考虑正解,将\(j,k\)看做横纵两维,那么转移时要做的操作就是保留一个矩阵,然后将其他位置置为\(0\)。
发现转移时有三种,\((j,k),(i,k),(i,j)\),第一种不用管,滚动数组自动继承,后两种发现都是\(i\),就相当于加入一行。
设\(s_{i}=\sum\limits_{j=1}^nf_{now,i,j}+f_{now,j,i}\),因为矩阵是对称的,这样可以做到\(O(n)\)加入一行。
具体的,用\(a_i\)记录\(f_{now,i}\)这一行中没有删去的,用\(b_i\)记录\(f_{now,,j}\)这一列没有删去的位置,然后用\(p,q\)再分别映射回原位置即可。
时间复杂度\(O(T(n^2+m))\)。
点此查看代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALFILE *InFile = freopen("in.in","r",stdin),*OutFile = freopen("out.out","w",stdout);
#else// FILE *InFile = stdin,*OutFile = stdout;FILE *InFile = freopen("color.in","r",stdin),*OutFile = freopen("color.out","w",stdout);
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
#define eb emplace_back
#define int long long
const int N = 5e3 + 10,M = 1e6 + 10,mod = 1e9 + 7;
struct limit{int l,x;};
vector<limit> lim[N];
int n,m,s[N],t[N];
vector<int> f,p,q,a[N],b[N];
inline void insert(int x,int y,int val){if(!val) return;int sz = f.size();f.eb(val),p.eb(x),q.eb(y);a[x].eb(sz);b[y].eb(sz);s[x] = (s[x] + val + mod)%mod,s[y] = (s[y] + val + mod) % mod;
}
inline void solve(){cin>>n>>m;rep(i,1,m,1){int l,r,x;cin>>l>>r>>x;lim[r].push_back({l,x});}insert(0,0,1);rep(i,0,n,1){int pl = 0,pr = 1e9,ql = 0,qr = 1e9;for(auto [j,x]:lim[i]){if(x == 1) pr = min(pr,j-1);if(x == 2) pl = max(pl,j),qr = min(qr,j-1);if(x == 3) ql = max(ql,j);}rep(j,0,i,1){if(j >= pl && j <= pr) continue;for(int x:a[j]) s[p[x]] = ((s[p[x]] - f[x])%mod + mod)%mod,s[q[x]] = ((s[q[x]] - f[x])%mod + mod)%mod,f[x] = 0;vector<int> ().swap(a[j]);}rep(j,0,i,1){if(j >= ql && j <= qr) continue;for(int x:b[j]) s[p[x]] = ((s[p[x]] - f[x])%mod + mod)%mod,s[q[x]] = ((s[q[x]] - f[x])%mod + mod)%mod,f[x] = 0;vector<int> ().swap(b[j]);}if(i < n){rep(j,0,i,1) t[j] = s[j];rep(j,0,i,1) insert(i,j,t[j]);}}int ans = 0;rep(i,0,n,1){ans = (ans + s[i] + mod)%mod,s[i] = 0;vector<int> ().swap(a[i]);vector<int> ().swap(b[i]);vector<limit> ().swap(lim[i]);}vector<int> ().swap(f);vector<int> ().swap(p);vector<int> ().swap(q);cout<<ans*500000004ll%mod<<'\n';
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);int T;cin>>T;while(T--) solve();
}
博弈
假设最后留下的三个数分别为\(a,b,c\),容易发现三个数的真实值并无影响,不妨设\(a\le b\le c\)。
分三种情况讨论。
-
三个值都相同,即\(a=b=c\)。那么先手直接输。
-
三个值都不相同,即\(a<b<c\),此时先手必胜。
证明:如果\(b=\frac{a+c}{2}\),则先手可以直接操作\(a,c\)到\(b\),则先手必胜。
考虑\(b<\frac{a+c}{2}\)和\(b>\frac{a+c}{2}\),发现这两种情况是等价的,此处只考虑\(b<\frac{a+c}{2}\)。
将其移动,假设\(a\)移动后的点为\(a^\prime\),\(c\)移动后的点为\(c^\prime\),由于\(a^\prime \le b\)时无影响,不考虑,考虑\(a^\prime = b\)的。
假如后手可以移动使得自己为处于必胜态,假设此时\(a^\prime\)的对应点为\(a^{\prime\prime}\),\(c^\prime\)的对应点为\(c^{\prime\prime}\),那么先手就可以直接移动到\(a^{\prime\prime},c^{\prime\prime}\),使得后手无法处于必胜态。
QED.
-
三个值中只有两个相同,发现\(a=b<c\)和\(a<b=c\)等价,不妨设\(a=b<c\)。此时当且仅当\(lowbit(c-a)\)为2的偶数次幂时先手必胜。
证明:先手必胜时当且仅当\((c-a)\bmod 2=0\),否则就会使得后者存在\(a<b<c\)的状态使得后手必胜。
假设\(f_{n}\)表示\(c-a=n\)时先手是否必胜,有\(f_{n}=!f_{\frac{n}{2}}\)。此时可以发现当且仅当\(n\)的最后一位\(1\)为偶数位时,\(f_{n}=true\)。
然后分别求\(a<b<c\)时的值和\(a=b<c\)时的答案即可。求\(a<b<c\)时直接容斥即可,求\(a=b<c\)的有两种做法,\(\log^2n\)的\(map\)做法:直接对于每一位开map;\(\log n\)的trie树上dp做法,具体的,考虑将偶数位的加上,奇数位的减去即可。
点此查看代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALFILE *InFile = freopen("in.in","r",stdin),*OutFile = freopen("out.out","w",stdout);
#else// FILE *InFile = stdin,*OutFile = stdout;FILE *InFile = freopen("game.in","r",stdin),*OutFile = freopen("game.out","w",stdout);
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
const int N = 5e5 + 10;
struct Trie{int tree[N*60][2],tot,siz[N*60];inline void insert(ll x){siz[0]++;int p = 0;rep(i,0,63,1){int k = (x>>i)&1ll;if(!tree[p][k]) tree[p][k] = ++tot,siz[tot] = 0;p = tree[p][k];siz[p]++;}}inline ll solve(ll x){ll res = 0;int p = 0,dep = 0;rep(i,0,63,1){int k = (x>>i)&1ll;if(!tree[p][k]) break;p = tree[p][k];dep++;res += ((dep&1)?1:-1)*siz[p];}return res;}inline void clear(){rep(i,0,tot,1) tree[i][0] = tree[i][1] = 0;tot = 0;siz[0] = 0;}
}T;
int n,ct[N],tot;ll a[N],w[N];
inline ll C(int x){return x<2?0ll:1ll*x*(x-1)/2;}
inline void solve(){cin>>n;rep(i,1,n,1) cin>>a[i];sort(a+1,a+1+n);tot = 0;rep(i,1,n,1){int ed = i;while(ed < n && a[ed + 1] == a[ed]) ed++;ct[++tot] = ed-i+1,w[tot] = a[i];i = ed;}ll sum1 = 0,sum2 = 0,ans = 0;rep(i,1,tot,1){ll c = C(sum2) - sum1;ans += c*ct[i];sum2 += ct[i];sum1 += C(ct[i]);}T.clear();rep(i,1,n,1) T.insert(a[i]);rep(i,1,tot,1){if(ct[i] < 2) continue;ll c = C(ct[i]);ans += c*T.solve(w[i]);}cout<<ans<<'\n';
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);int T;cin>>T;while(T--) solve();
}
后缀数组
60pts:
用FHQ维护那\(m\)个修改操作,时间复杂度 \(m\log n\)。实现是参考文艺平衡树。然后统计所有 \(rk[a[i]+1]<rk[a[i+1]+1]\)的数量,答案是\(2^k\)。
没写。
p