MaskLLM：英伟达出品，用于大模型的可学习`N:M`稀疏化 | NeurIPS24

news/2024/11/20 9:12:52/文章来源:https://www.cnblogs.com/VincentLee/p/18556050

来源：晓飞的算法工程笔记公众号，转载请注明出处

论文: MaskLLM: Learnable Semi-Structured Sparsity for Large Language Models

论文地址：https://arxiv.org/abs/2409.17481
论文代码：https://github.com/NVlabs/MaskLLM

创新性

提出一种可学习的LLM半结构化剪枝方法MaskLLM，旨在充分利用大规模数据集来学习准确的N:M掩码，适用于通用剪枝和领域特定剪枝。
此外，该框架促进了跨不同任务的稀疏模式迁移学习，从而实现稀疏性的高效训练。

内容概述

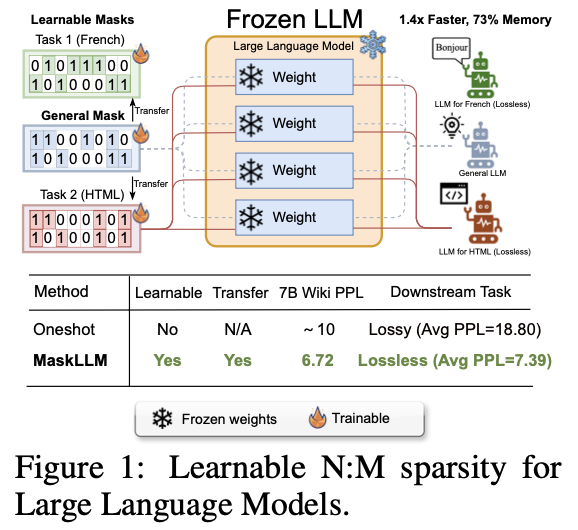
大型语言模型（LLMs）的特点是其巨大的参数数量，这通常会导致显著的冗余。论文提出一种可学习的剪枝方法MaskLLM，在LLMs中建立半结构化（或N:M，在M个连续参数中有N个非零值的模式）稀疏性，以减少推理过程中的计算开销。

MaskLLM通过Gumbel Softmax采样将N:M模式稀疏化显式建模为可学习的分布，可在大规模数据集上的端到端训练，并提供了两个显著的优势：

高质量的掩码，能够有效扩展到大型数据集并学习准确的掩码。
可转移性，掩码分布的概率建模使得稀疏性在不同领域或任务之间的迁移学习成为可能。

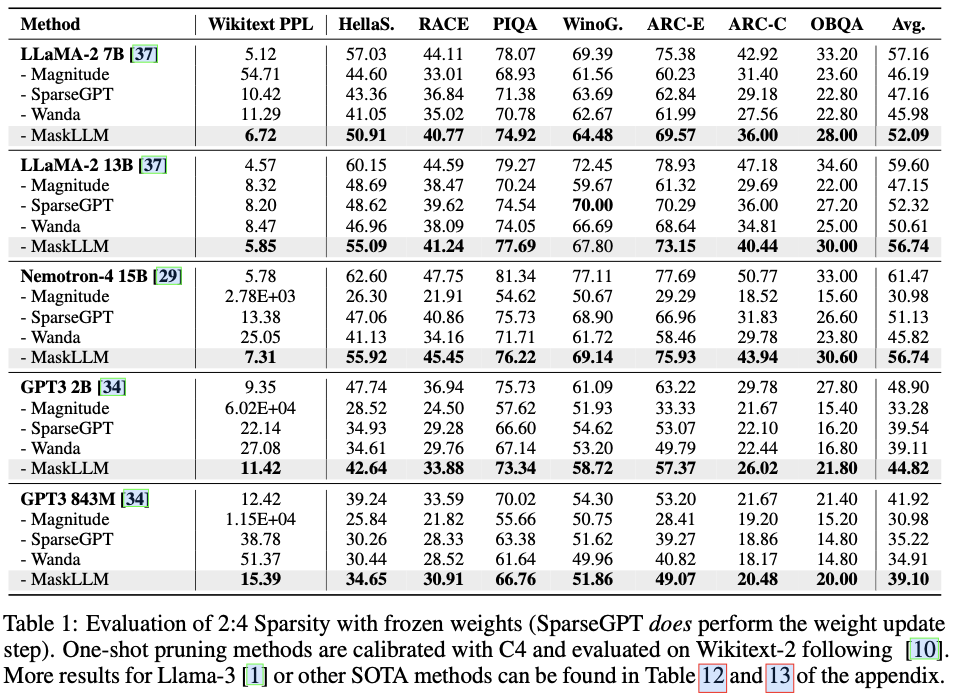
在不同的LLMs上使用2:4稀疏性评估MaskLLM，如LLaMA-2、Nemotron-4和GPT-3，参数规模从843M到15B不等。实证结果显示，相较于最先进的方法有显著改进，MaskLLM通过冻结权重并学习掩码实现了显著更低的6.72困惑度。

MaskLLM

`N:M` 稀疏性

N:M模式稀疏化会对LLM施加限制，即每一组连续的M个参数中最多只能有N个非零值。这个任务可以被转换为一个掩码选择问题，候选集的大小为 \(|\mathbf{S}|=\binom{M}{N} = \frac{M!}{N!(M-N)!}\) ，其中 \(|\mathbf{S}|\) 表示候选集的大小， \(\binom{M}{N}\) 表示潜在N:M掩码的组合数。

对于2:4稀疏性，二进制掩码 \(\mathcal{M}\) 必须恰好包含两个零，从而形成一个离散的候选集 \(\mathbf{S}^{2:4}\) ，其大小为 \(|\mathbf{S}^{2:4}|=\binom{4}{2}=6\) 个候选：

\[\begin{align} \mathbf{S}^{2:4} & = \{\mathcal{M} \in \mathbb{B}^{1\times4} | \sum \mathcal{M} = 2\} = \{\hat{\mathcal{M}}_1, \hat{\mathcal{M}}_2, \hat{\mathcal{M}}_3, \hat{\mathcal{M}}_4, \hat{\mathcal{M}}_5, \hat{\mathcal{M}}_6 \} \\ & = \{[1,1,0,0], [1,0,1,0], [1,0,0,1],[0,1,0,1],[0,1,1,0],[0,0,1,1]\}. \end{align} \]

对于一个LLM，存在大量的参数块，记为 \(\{\mathcal{W}_i\}\) ，每个参数块都需要选择相应的掩码 \(\{\mathcal{M}_i\}\) 。对于剪枝后的性能，为N:M稀疏性定义以下损失目标：

\[\begin{equation} \{\mathcal{M}_i^{*}\} = \underset{\{\mathcal{M}_i | \mathcal{M}_i \in \mathbf{S}^{2:4}\} }{argmin} \mathbb{E}_{x\sim p(x)} \left[ \mathcal{L}_{LM}(x; \{\mathcal{W}_i \odot \mathcal{M}_i\}) \right], \label{eqn:objective} \end{equation} \]

其中 \(\mathcal{L}_{LM}\) 指的是预训练的语言建模损失。操作符 \(\odot\) 表示逐元素乘法，用于掩码部分参数以进行稀疏化。

可学习半监督稀疏性

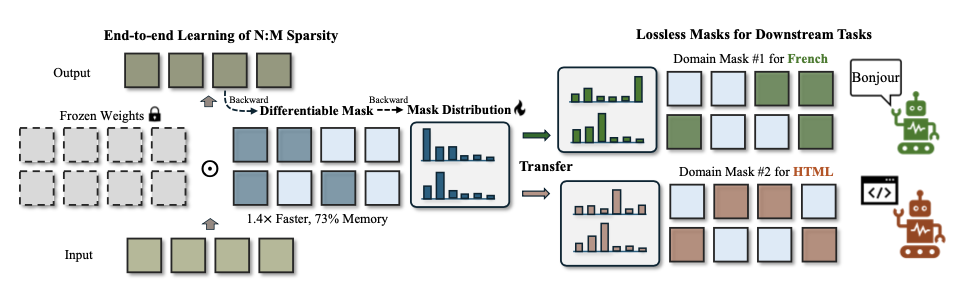
在LLM的背景下，由于掩码选择的不可微分特性和庞大的参数规模，找到最佳掩码组合 \({\mathcal{M}^*}\) 可能极具挑战性。为此，论文将掩码选择转化为一个采样过程。

直接确定参数块的确切最佳掩码是不可行的，因为修剪后的LLM的行为还依赖于其他参数块的修剪。但可以独立地为每个块采样掩码，并在修剪后评估整体模型质量。

定义一个具有类别概率 \(p_1, p_2, \ldots p_{|\mathcal{S}|}\) 的类别分布，满足 \(\sum_{j} p_j=1\) 。在随机采样阶段，如果某个掩码在修剪过程中表现出良好的质量，那么通过增加被采样掩码的概率来调整类别分布是合理的。

通过足够的采样和更新，最终会得到一组分布，其中高概率的掩码更有可能在修剪后保持良好的质量。

从形式上讲，从随机采样的角度建模上述公式中的组合问题：

\[\begin{equation} \{p^{*}(\mathcal{M}_i)\} = \underset{\{p(\mathcal{M}_i)\}}{argmin}\ \mathbb{E}_{x\sim p(x), \mathcal{M}_i \sim p(\mathcal{M}_i)} \left[ \mathcal{L}_{LM}(x; \{\mathcal{W}_i \odot \mathcal{M}_i\}) \right], \label{eqn:objective_sampling} \end{equation} \]

如果能够获得关于该分布的梯度，那么上述目标可以通过梯度下降进行优化，但从类别分布中抽取样本仍然是不可微分的。

可微分掩码采样

Gumbel Max能有效地建模采样操作，将采样的随机性解耦为一个噪声变量 \(\epsilon\)。根据类别分布 \(p\) 抽取样本，生成用于采样的one-hot索引 \(y\) ：

\[\begin{equation} y=\text{onehot}(\underset{i}{argmax} [\log(p_i) + g_i]), \; g_i=-\log(-\log \epsilon_i), \; \epsilon_i\sim U(0, 1), \label{eqn:gumbel_max} \end{equation} \]

其中 \(\epsilon_i\) 是遵循均匀分布的随机噪声，而 \(g_i = -\log(-\log \epsilon_i)\) 被称为Gumbel噪声。Gumbel Max将采样的随机性参数化为一个独立变量 \(g_i\)，可微分采样的唯一问题出在 \({argmax}\) 和one-hot操作。

为了解决这个问题，通过Gumbel Softmax来近似Softmax索引，从而得到一个平滑且可微分的索引 \(\tilde{\mathbf{y}}=[\tilde{y}_1, \tilde{y}_2, \ldots, \tilde{y}_{|\mathbf{S}|}]\) ：

\[\begin{equation} \tilde{y}_i = \frac{\exp((\log(p_i) + g_i) / \tau)}{\sum_j \exp( (\log(p_j) + g_j) / \tau ) }. \label{eqn:gumbel_softmax} \end{equation} \]

温度参数 \(\tau\) 是一个超参数，用于控制采样索引的硬度。当 \(\tau \rightarrow 0\) 时，软索引将更接近于一个one-hot向量，从而导致 \(\tilde{y}_i\rightarrow y_i\) 。

将软索引 \(\tilde{\mathbf{y}}\) 视为行向量，将掩码集合 \(\mathbf{S}\) 视为一个矩阵，其中每一行 \(i\) 指代第 \(i\) 个候选掩码 \(\hat{\mathcal{M}}_i\) ，通过简单的矩阵乘法很容易构造出一个可微分的掩码：

\[\begin{equation} \tilde{\mathcal{M}} = \tilde{\mathbf{y}} \times \mathbf{S}=\sum_{i=1}^{|\mathbf{S}|} \tilde{y}_i \cdot \hat{\mathcal{M}}_i.\label{eqn:diff_mask} \end{equation} \]

这个操作根据软索引生成候选掩码的加权平均，所有操作（包括采样和加权平均）都是可微分的，并且相对于概率 \(p\) 的梯度可以很容易地计算，能够使用可微分掩码 \(\tilde{\mathcal{M}}\) 来优化公式4中的采样问题。

学习LLMs的掩码

基于从基础分布 \(p\) 中采样的可微分掩码，梯度流可以轻松到达概率 \(p_i\) ，使其成为系统中的一个可优化变量。但通常并不直接学习从logits生成概率，而是学习带有缩放因子 \(\kappa\) 的logits \(\pi_i\) ，通过公式 \(p_i = \frac{\exp(\pi_i \cdot \kappa)}{\sum_j \exp( \pi_j \cdot \kappa )}\) 来产生概率。

缩放因子 \(\kappa\) 将用于平衡logits和Gumbel噪声的相对大小，从而控制采样的随机性。在训练过程中，所有参数块 \(\{\mathcal{W}_i\}\) 都与相应的分布 \(\{p_\pi(\mathcal{M}_i)\}\) 相关联，并且以端到端的方式学习到最佳分布。

但在多个大语言模型上的实验发现了一个关于可学习掩码的新问题：由于修剪操作会在网络中产生零参数，梯度可能会消失。

为了解决这个问题，引入了稀疏权重正则化，它在剩余权重中保持适当大的幅度，从而导致以下学习目标：

\[\begin{equation} \min_{\{p_{\pi}(\mathcal{M}_i)\}} \mathbb{E}_{x, \tilde{\mathcal{M}}_i \sim p_{\pi}(\mathcal{M}_i)} \left[ \mathcal{L}_{LM}(x; \{\mathcal{W}_i \odot \tilde{\mathcal{M}}_i\}) \right] - \lambda \sum_i \|\mathcal{W}_i \odot \tilde{\mathcal{M}}_i\|^2_2. \label{eqn:final_objective} \end{equation} \]

由 \(\lambda\) 加权的正则化项鼓励在修剪后保持较大的幅度。

稀疏性的迁移学习

迁移学习是深度学习中最流行的范式之一，而稀疏性的迁移学习则是通过预计算的掩码来构造新的掩码。

论文提出了用于初始化分布的掩码先验（Mask Prior），可以大幅提升训练效率和质量。掩码先验可以通过一次性剪枝的方法获得，例如幅值剪枝、SparseGPT和Wanda。

给定一个先验掩码 \(\mathcal{M}_0\) ，计算其与所有候选掩码的相似度：

\[\begin{equation} \text{sim}(\mathcal{M}_0, \hat{\mathcal{M}}_i) = \mathcal{M}_0 \hat{\mathcal{M}}_i^\top - \frac{1}{|\mathbf{S}|} \sum_i (\mathcal{M}_i \hat{\mathcal{M}}^\top) = \mathcal{M}_i \hat{\mathcal{M}}^\top - (N/2), \end{equation} \]

对于与先验掩码高度相似的候选掩码，在初始化阶段提高其概率：

\[\begin{equation} \pi_i^{\prime} = \pi_i + \sigma(\pi)* \text{sim}(\mathcal{M}_0, \hat{\mathcal{M}}_i) * \alpha, \label{eqn:prior_mask} \end{equation} \]

其中， \(\sigma(o)\) 是logits的标准差， \(\alpha\) 是控制先验强度的超参数。当 \(\alpha=0\) 时，代表在没有任何先验的情况下学习可微的掩码。