CF2025

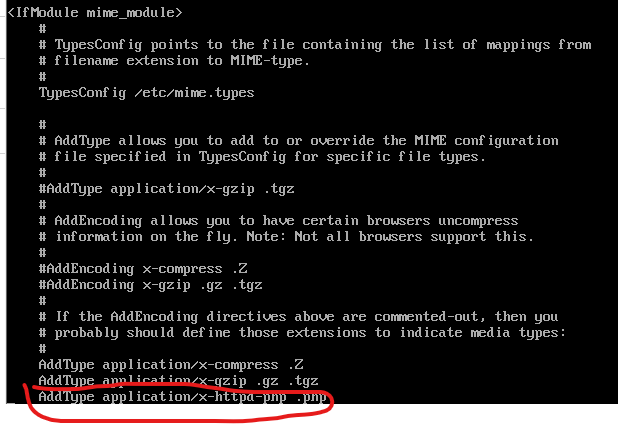
更好的观看体验：Here

A

你要生成两个字符串。
起初有两个空串，你可以在任意一个后加任意字母，或者把一个串复制并覆盖掉另一个串。
求最小操作次数，使得两个串和给定的两个串相同。
$n,m\le 100$

注意到覆盖操作显然只会发生至多一次。
故覆盖 lcp 是最优的。
值得注意的是，可以不覆盖，此时无 lcp。

B

$f_{n,0}=f_{n,n}=1,f_{n,m}=f_{n-1,m-1}+f_{n-1,m-1}$。
给定 $n,m$，求 $f_{n,m}$。
$t\le 10^5,m\le n\le 10^5$

题解给了暴力展开转移式变为二项式系数的做法。
考虑网格图，枚举转移起点有：
\(\sum\limits_{i=0}^{n} \binom{m}{i}=\sum\limits_{i=0}^{m}\binom{m}{i}=2^{m}\)。

C

有一个可重集合，支持如下选取方式：
第一次任选，设上一次选了 $x$，则下一次可选 $x,x+1$。
要求选的数的众数不超过 k，求最长的选数个数。
$n\le 10^5$

显然是选择连续的不超过 k 种数全部选择。
排序后双指针一下就可以。
有一说一双指针算是这种问题的最好的实现方式了。

D

有一个长为 n 的任务序列，上面有三种任务，分别是分发灵光点，检查力量和检查智力。
当你获得灵光点的时候，你可以给力量和智力中的一个加一点，这种操作只有 m 个。
检查某一数值为，若你当前的该数值不小于检查标准数值，则通过。
请最大化通过检查个数。
$n\le 10^6,m\le 5\times 10^3$

检查不具有单调性，因为可以从中间某个任务开始做。
应该把转移式写出来看看的。

直接写朴素的转移式，设 \(f_{i,j}\) 表示考虑了前 \(i\) 个任务，其中 \(j\) 个分配给力量的最优值。
转移显然，分别是分配点数和检查任务，第一个暴力做即可，第二个是区间加。
区间加也只需打一个标记，可以看作变换设的状态为考虑了前 \(i\) 个加灵光点。

E

有 n 种花色和 m 种等级组成的 $n\times m$ 张牌。
规定牌的序：
若两张牌花色不同，那么其中 1 花色的那张更大。
若两张牌花色相同，等级高的那张更大。
现在要把这些牌均分给 A 和 B，要求存在一种配对方案，使得每个对都是 A 的牌比 B 的大。
求这样的分配牌的方案数。
$n,m\le 500$
保证 m 为偶数。

分配形如：
对于 1 来说，要至少配对，可能 A 有更多。
对于其他花色来说，至少配对，可能 B 有更多。
这两种方案是等价的，只需反过来做合法括号序列即可。
值得注意的是，应用多步容斥可以把 dp 变为组合数，做到 \(\mathcal O(m)\)。
然后需要做一个背包，使得 A 更多的，和其他花色中 B 更多的之和相等。
背包形如一个泛化物品合并 n 次，可以用多项式快速幂做到 \(\mathcal O(m\log m\log n)\)。
嗯，反正 \(\mathcal O(nm^{2})\) 的复杂度就是最劣的了。

F

[Luogu](https://www.luogu.com.cn/problem/CF2025F)
给定一张无向图，要求对该图重定向，使得出度为奇数的点个数最少。
输出方案。
$n,m\le 3\times 10^5$

思路解析

奇偶性图论题，是不是很熟悉？？？
注意到这个限制实际上是非常弱的，感觉很容易调整。
答案会走向两个极端，一种是不可想的贪心流一侧，另一种是结论式的构造。
考虑下界并试图构造。
把问题放到 dfs 树（无向图无横叉边）上去考虑，调整。

正解

设一个点在一种方案中的出度为 \(d_{i}\)，则答案为 \(\sum\limits d_{i}\bmod 2\)。
显然有一个下界：
\((\sum\limits d_{i} \bmod 2)\bmod 2=\left( \sum\limits d_{i} \right)\bmod 2\)。
\(\sum\limits d_{i} \bmod 2)\geq\left( \sum\limits d_{i} \right)\bmod 2\)。

考虑对每个连通块去尝试构造这个下界。
奇偶性的问题考虑任意一棵搜索树。
（实际上这里的思维是一个由一般到特殊的过程）
注意到无向图在搜索树上
那么考虑归纳的构造，设 \(solve(u)\) 表示对于 u 子树内调整后除 u 以外都是偶数。
如果这一步能做到的话，只需把树边尽儿子挂到 u 上，归纳起来即可构造。
这样最后就构造出只有一个点不一定是偶数，于是卡到了下界。

问题在于这道题过于好调整，只要提供一个序就很好去优化（实际上甚至不需要考虑构造），这时候 dfs 树就是很优的了。

G

[Luogu](https://www.luogu.com.cn/problem/CF2025G)
对于一个角色和盾的集合，我们能用血量来描述角色和盾。
每个角色至多持有一个盾。
每次对所有角色和盾造成相同的伤害，且总伤害为 1，即每个实体收到 $\frac{1}{a+b}$ 的伤害。
盾破裂当且仅当自身血量耗尽或持有它的角色死亡。
分配盾给角色，最大化他们支撑的回合数。
起初为空，动态插入角色和盾，每次插入后求出答案。
$q\le 3\times 10^5,a_i\le 10^9$

相当长，有一点 trick 的套路题。

思路解析

考虑模拟。
推式子。
贪心最优。
进行贪心过程的分析并优化，建模。
分块维护。

正解

考虑已经给定了关系怎么做。
发现这个分数在打掉一点伤害前不会变化，则可以变化为对每一点伤害的存活实体数计数。
拆贡献，这样每个实体恰好被计算了 \(a_{i}\) 次，故总式子为 \(\sum\limits a_{i}+\sum\limits \min(a_{i},b_{i})\)。
另一个角度，由于每轮的伤害总和确定，且伤害不会打到死亡的人身上，故总轮数也就是总血量了。

只需考虑第二个式子，想想什么时候最优。
发现只需两者都排序后从大到小匹配，邻项交换容易证明。

直接维护看起来是困难的，我们从静态的问题上刻画该过程。
发现可以把二者一起排序，扫描线的同时维护角色个数和盾个数的差即可。
这样去除了 \(\min(a,b)\) 必须匹配起来才能计算的过程，而是可以直接通过扫描线扫到的时候来确认。
这样我们确认了一个流程，只依赖于前缀差这唯一一个属性，且每一位是否贡献进来只取决于这个前缀差。

离散化（等值不同）并维护前缀和数组，支持单点激活，区间 \(\pm 1\)，维护所有 \(\geq 0\) 和 \(\leq 0\) 的和。
[[【纪中模拟】树上二维偏序问题]] 这道题我写过了，只需均摊地值域分块即可。