人工智能之深度学习基础——反向传播（Backpropagation）

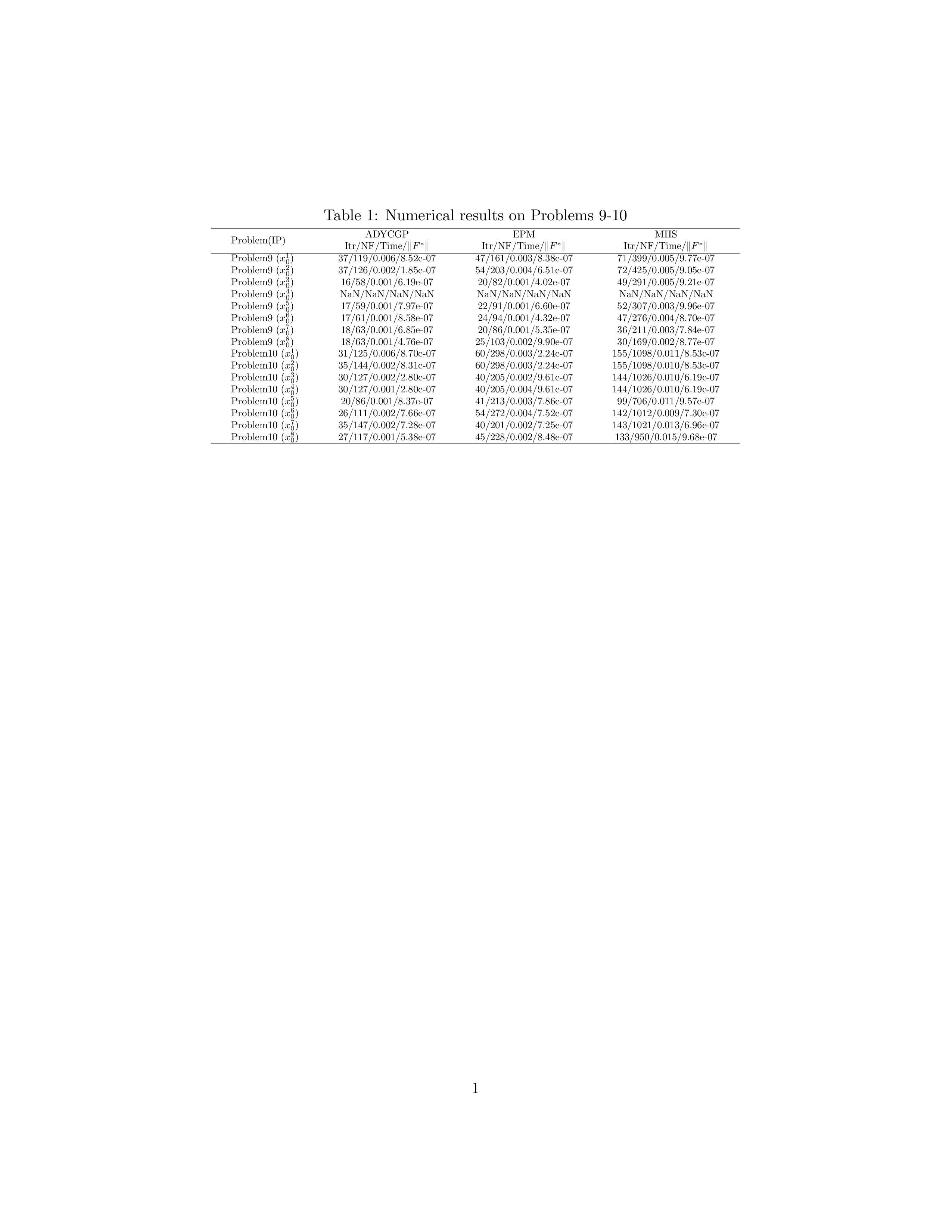
反向传播（Backpropagation）

反向传播是神经网络的核心算法之一，用于通过误差反传调整网络参数，从而最小化损失函数。它是一种基于链式法则的高效梯度计算方法，是训练神经网络的关键步骤。

1. 反向传播的基本步骤

1.1 前向传播

在前向传播过程中，输入数据从输入层经过隐藏层传递到输出层，计算出模型的预测值 y_pred和损失值 L。

1.2 损失计算

损失函数（如均方误差或交叉熵）衡量模型的预测值与真实值之间的差异：

L=Loss(y_pred​,y_true​)

1.3 反向传播

根据链式法则，计算损失函数相对于每个参数的梯度 ∂L/∂w，从输出层向输入层逐层反向传播。

1.4 参数更新

利用梯度下降等优化算法，通过梯度信息更新每层的权重和偏置：

w=w−η⋅∂w/∂L​

其中：

• w：参数；
• η：学习率。

2. 反向传播的数学推导

2.1 神经网络的层间关系

假设神经网络的某一层：z^(l)=W^(l)a^(l−1)+b^(l) 

　　　　　　　　　　 a^(l)=f(z^(l))

其中：

• z^(l)：隐藏层的线性输出；
• W^(l)：权重矩阵；
• b^(l)：偏置向量；
• a^(l)：激活值；
• f：激活函数。

2.2 损失函数

以均方误差为例：

2.3 输出层梯度

输出层的误差：

 

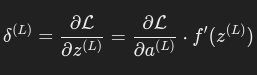
其中：

 

2.4 隐藏层梯度

隐藏层的误差通过链式法则传播：

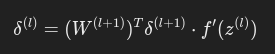
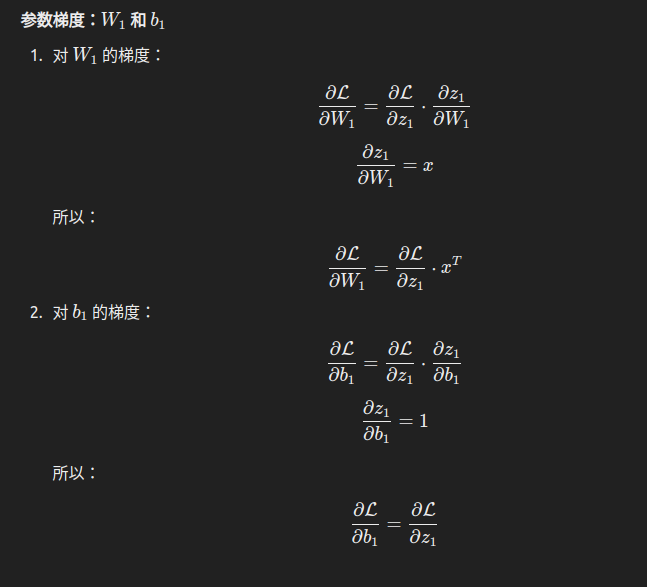
2.5 梯度计算

权重和偏置的梯度为：

 

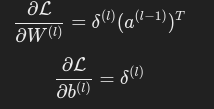
3. 反向传播的流程

1. 前向传播：计算每一层的线性输出 z^(l)、激活值 a^(l)，直到输出层。
2. 计算损失：使用目标函数（如交叉熵、均方误差）计算预测值与真实值的差距。
3. 反向传播：
   • 从输出层开始，计算每一层的误差 δ^(l)；
   • 通过误差传播公式，将误差逐层传递至输入层。
4. 更新参数：利用梯度下降算法更新每层的权重 W^(l) 和偏置 b^(l)。

4. 反向传播的简单例子

问题

构造一个简单的单隐藏层神经网络，输入数据 x=[0.5,0.1]，目标输出 y_true=0.6，激活函数使用 Sigmoid。

模型结构

1. 输入层：2 个神经元。
2. 隐藏层：2 个神经元。
3. 输出层：1 个神经元。

参数初始化

 

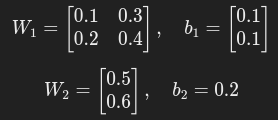
 计算步骤

 σ这里是SIgmoid函数

 

反向传播求导详细计算

 

反向传播的核心是计算损失函数对网络参数的梯度，即 ∂L/∂W​ 和 ∂L/∂b。以下详细解析各步骤的求导，逐步展开每个公式的由来。

1. 网络的定义

 单隐藏层神经网络

 2. 输出层的梯度计算

 损失函数对输出层的梯度

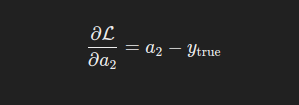
 激活值对线性输出的梯度

激活函数是 Sigmoid：

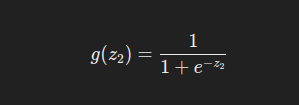
Sigmoid 的导数为： 

 

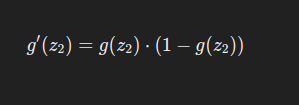
因此： 

 

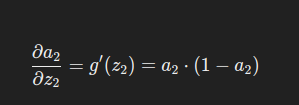
链式法则：损失对线性输出的梯度

根据链式法则：

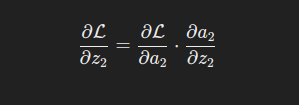
代入：

  

 

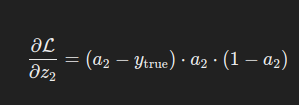
3. 隐藏层的梯度计算

损失对隐藏层激活值的梯度

输出层误差会传播到隐藏层：

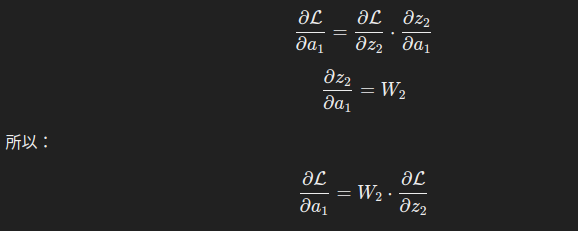
 隐藏层激活值对线性输出的梯度

活函数为 Sigmoid：

 

 

 

 

总结

反向传播通过链式法则逐层计算梯度，并利用梯度下降法更新网络参数，最终最小化损失函数。反向传播算法是现代深度学习的基石，结合优化算法（如 SGD、Adam）可以高效训练复杂的神经网络模型。